
Quelle: Wikimedia Commons File:Georg Cantor3.jpg, gemeinfrei
Die Mengenlehre als ein mögliches Fundament der Mathematik
Die Mächtigkeit unendlicher Mengen
Ein formales System für Mengen
Drei einfache Grundaxiome für Mengen
Russels Paradoxon
Das Aussonderungsaxiom rettet das System
In seinem berühmten Vortrag aus dem Jahr 1900 entwarf David Hilbert die Vision eines mathematischen Systems, das von gewissen Axiomen ausgehend in der Lage ist, die gesamte Mathematik zu begründen und zu umfassen. Die Arbeiten von Gödel, Turing und anderen haben seit 1931 gezeigt, dass diese Vision in dieser Form nicht umsetzbar ist. Jedes widerspruchsfreie formale System, das in der Lage ist, zumindest die Addition und Multiplikation der natürlichen Zahlen zu beschreiben, ist unvollständig. Es gibt wohlgeformte Aussagen, die sich innerhalb des Systems nicht beweisen und nicht widerlegen lassen. Daher kann eine solche nicht-entscheidbare Aussage (oder alternativ ihr Gegenteil) als weiteres Axiom dem System hinzugefügt werden. Auf diese Weise kann man im Prinzip immer neue Axiome hinzunehmen, ohne dass dadurch jemals die Unvollständigkeit des Systems beseitigt würde.
Es gibt also unendlich viele formale Systeme, die der Mathematik zugrundegelegt werden könnten. Kein Einziges dieser Systeme ist wahr oder falsch. Je nach untersuchtem Problem können aber die einzelnen formalen Systeme unterschiedlich nützlich sein.
Wenn aber unendlich viele formale Systeme möglich sind, wird dann nicht die gesamte Mathematik vollkommen beliebig? Arbeitet jedes Spezialgebiet der Mathematik mit eigenen, speziell auf dieses Gebiet zugeschnittenen Axiomensystemen, ohne dass diese verschiedenen Systeme etwas miteinander zu tun haben?
Die Geschichte der Mathematik zeigt, dass das nicht der Fall ist. So waren früher die Geometrie und das Rechnen mit Zahlen (Arithmetik) getrennte Gebiete. Die Einführung von Koordinaten und neuer Begriffe wie z.B. mehrdimensionale Räume, Vektoren und Funktionen führte jedoch schließlich zu einer Vereinigung beider Gebiete. Ähnliche Beobachtungen macht man auch in anderen Teilbereichen der Mathematik. Große, hartnäckige Probleme wie z.B. die Fermatsche Vermutung werden oft dadurch gelöst, dass Zusammenhänge zwischen verschiedenen Teilgebieten erkannt werden. Ein Beispiel dafür ist der Zusammenhang zwischen diophantischen Gleichungen und auflistbaren (rekursiv aufzählbaren) Mengen (siehe Kapitel 3.5).
Gibt es also doch so etwas wie ein gemeinsames Fundament, auf dem zumindest ein Teil der bekannten Mathematik aufbaut. Ist Hilberts Vision vielleicht doch gar nicht so abwegig?
Im Lauf der letzten 100 Jahre gab es mehrere Versuche, ein solches Fundament aufzubauen. Die meisten dieser Versuche sind gescheitert, zum Teil auch deswegen, weil sie den Anspruch hatten, die gesamte Mathematik zu umfassen. Schließlich aber gelang es doch, ein Fundament zu errichten, das praktisch für die gesamte bekannte Mathematik eine solide Grundlage zu schaffen scheint: die Mengenlehre!
Die Mengenlehre ist allerdings nicht die einzige Möglichkeit, ein solches Fundament zu bauen. Andere moderne Versuche sind die category theory und die Typentheorie. Welche dieser Möglichkeiten das beste Fundament darstellt, wird heute kontrovers diskutiert, und das letzte Wort ist sicher noch nicht gesprochen. Es ist auch durchaus möglich, dass in Zukunft noch bessere Möglichkeiten gefunden werden. Da die Mengenlehre heute die am weitesten verbreitete und allgemein anerkannte Möglichkeit für ein Fundament der Mathematik ist, werden wir uns im Folgenden auf sie konzentrieren.
Wie tragfähig ist die Mengenlehre? Man ist heute der Meinung, dass praktisch die gesamte klassische Mathematik mit den Begriffen der Mengenlehre beschrieben werden kann, und dass die Axiome der Mengenlehre ein sehr mächtiges Fundament bilden, das sich mittlerweile als sehr stabil und tragfähig erwiesen hat. Ein Grund dafür liegt sicher darin, dass die Mengenlehre mit aktual-unendlichen Objekten umgehen kann. Beispielsweise kann der Begriff der Menge aller natürlichen Zahlen in der Mengenlehre formuliert werden. Ebenso kann von allen Eigenschaften der natürlichen Zahlen gesprochen werden (dies ist die Menge aller Teilmengen der Menge der Natürlichen Zahlen). In der Peano-Arithmetik können solche Begriffe nicht formuliert werden – hier kann mit der Unendlichkeit nur im Sinne potentieller Unendlichkeit umgegangen werden, d.h. man kann über die Nachfolger-Funktion beliebig weit in den natürlichen Zahlen fortschreiten, ohne sie allerdings je komplett erfassen zu können. Welche Folgen dies hat, werden wir in den folgenden Kapiteln noch sehen.
Die Mengenlehre kann zwar nach Gödel nicht die gesamte denkbare Mathematik umfassen, aber sie könnte so etwas wie den harten Kern bilden – eine Art minimalen Sprach - und Wissensschatz, auf dem Mathematik aufbauen kann. Wir wollen uns daher in diesem und in den folgenden Kapiteln genauer mit der Mengenlehre und ihren Axiomen beschäftigen.
Die Ursprünge der Mengenlehre reichen in das Jahr 1872 zurück, in dem Georg Cantor den folgenden
wichtigen Satz über Fourierreihen bewies: Zwei Fourierreihen, die an allen Punkten
der reellen Zahlengeraden mit endlich vielen Ausnahme-Punkten dem gleichen Grenzwert
zustreben, sind identisch, d.h. sie haben identische Koeffizienten.

Quelle:
Wikimedia Commons File:Georg Cantor3.jpg,
gemeinfrei
Cantor überlegte nun, ob man nicht über endlich viele Ausnahmepunkte hinausgehen kann, ohne dass die Fourierreihen ihre Gleichheit verlieren. Im ersten Schritt bewies Cantor, dass auch alle Punkte der Form \(1, 1/2, 1/3, ... \) (allgemein also \(1/n\) ) als Ausnahmepunkte zulässig sind – es dürfen also auch unendlich viele Ausnahmepunkte sein. Im obigen Beispiel konvergieren die Ausnahmepunkte dabei auf den sogenannten Häufungspunkt \(0\) zu. Allgemein sind auch endlich viele Häufungspunkte erlaubt, also z.B. die Punkte an den Stellen \( 1/n + 1/m \) .
Dürfen die Ausnahmepunkte auch unendlich viele Häufungspunkte besitzen? Wir merken, wie alle diese Fragen darum kreisen, welche Struktur die Ausnahmepunkte aufweisen dürfen. An wieviel Stellen dürfen sie sich unendlich eng zusammendrängen? Die Idee, Begriffe wie die Menge der Ausnahmepunkte oder die Menge der Häufungspunkte der Menge der Ausnahmepunkte zu verwenden, war geboren. Dabei konnten diese Mengen auch unendlich viele Punkte enthalten.
Cantor begann, sich allgemeiner mit dem Mengenbegriff zu beschäftigen. Er definierte diesen Begriff dabei so:
Dabei interessierte ihn besonders, eine Methode zu finden, die die Mächtigkeit (also die Größe) einer Menge charakterisieren konnte (wie mächtig konnte die Menge der Häufungspunkte werden, so dass die Fourierreihen identisch blieben?). Besonders interessant waren dabei unendliche Mengen, denn bei endlichen Mengen brauchte man ja nur die Elemente der Menge zu zählen.
An einem Punkt seiner Überlegungen stieß Cantor schließlich auf die folgende Frage:
Die Antwort auf diese Frage hängt natürlich davon ab, was man unter der Mächtigkeit einer Menge versteht. Cantors Idee, die Mächtigkeit zweier Mengen zu vergleichen, war die Folgende:
Für endliche Mengen ist diese Definition unmittelbar einsichtig, denn man überprüft ja damit, ob eine Menge mehr Elemente als eine andere Menge enthält. Bei unendlichen Mengen dagegen erlebt man einige Überaschungen.
Die erste Überaschung erlebt man, wenn man die Menge der natürlichen Zahlen (also 1, 2, 3, 4, ...) mit der Menge der geraden natürlichen Zahlen (also 2, 4, 6, ...) vergleicht. Man sieht sofort, dass man jede natürliche Zahl eindeutig einer geraden natürlichen Zahl zuordnen kann, indem man einfach die natürliche Zahl verdoppelt. In diesem Sinn sind die beiden Mengen also gleich mächtig, obwohl man intuitiv sagen würde, dass die eine Menge doppelt so groß wie die andere Menge sein muss. Der oben definierte Mächtigkeits-Begriff weicht hier also von unserer Intuition ab.
Eine zweite Überaschung erlebt man, wenn man die Menge der natürlichen Zahlen
mit der Menge der positiven rationalen Zahlen (also Brüchen)
vergleicht. Cantor stellte fest, dass man die natürlichen Zahlen eins-zu-eins
den positiven Brüchen zuordnen kann, wie das folgende Bild zeigt (doppelte Brüche lässt man dabei einfach weg):
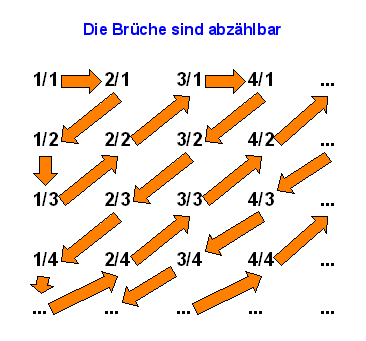
Man kann also alle Brüche in einer unendlich langen Liste aufführen und sie durchnummerieren: \begin{equation} \frac{1}{1}, \frac{2}{1}, \frac{1}{2}, \frac{1}{3}, \frac{2}{2}, \frac{3}{1}, \frac{4}{1}, \frac{3}{2}, \frac{2}{3}, \frac{1}{4} , ... \end{equation} (doppelte wie 1 und 2/2 etc. müsste man hier noch streichen). Die Menge der rationalen Zahlen ist also gleich mächtig wie die Menge der natürlichen Zahlen, obwohl die rationalen Zahlen dicht auf dem Zahlenstrahl liegen (d.h. in beliebig kleinen Intervallen auf dem Zahlenstrahl liegen immer unendlich viele rationale Zahlen).
Cantor ging nun einen Schritt weiter und untersuchte die reellen Zahlen, also die Zahlen, die auch unendlich viele Dezimalstellen hinter dem Komma haben können und die nicht unbedingt als Bruch darstellbar sein müssen (z.B die Zahl \( \pi \) aus Kapitel 3.3 oder auch die Zahl \( \sqrt{2} \)). Ist die Menge dieser Zahlen auch genauso mächtig wie die Menge der natürlichen Zahlen?
Cantor zeigte im Jahr 1874, dass die reellen Zahlen eine größere Mächtigkeit als die natürlichen Zahlen (und damit auch größer als die rationalen Zahlen) aufweisen. Den Beweis führte Cantor mit Hilfe seines berühmten Diagonalverfahrens, dass wir bereits in Kapitel 2.3 kennengelernt haben. Der Beweis geht so:
Angenommen, wir könnten die reellen Zahlen in einer unendlich langen Liste komplett aufführen (die Zeilennummer in der Liste wäre dann die zugeordnete natürliche Zahl). Die Liste sähe dann etwa so aus:
Dabei steht \(a_1 \) für die erste Dezimalstelle der ersten reellen Zahl \(a\) in der Liste usw.. Nun können wir eine neue reelle Zahl konstruieren, indem wir die Dezimalstellen entlang der Diagonalen der obigen Liste aufsammeln, jede einzelne von ihnen abändern (z.B. um eins erhöhen oder erniedrigen) und dann als die Dezimalstellen einer neuen Zahl aneinanderfügen: \( 0, (a_1+1) (b_2+1) ... \).
Diese neue Zahl weicht dann garantiert in der ersten Dezimalstelle von \(a\) ab, in der zweiten Dezimalstelle von \(b\) usw., d.h. sie unterscheidet sich von jeder Zahl in der Liste. Damit haben wir gerade eine reelle Zahl konstruiert, die nicht in der Liste enthalten ist. Die Liste ist also unvollständig. Auch Aufnehmen dieser neuen Zahl in die Liste macht die Liste nicht vollständig, denn die Konstruktion lässt sich mit der neuen Liste wiederholen. Damit ist klar, dass bei jedem Versuch, die natürlichen Zahlen eins-zu-eins den reellen Zahlen zuzuordnen, immer unendlich viele reelle Zahlen übrig bleiben. Die Ursache, warum es eine eins-zu-eins-Zuordnung von natürlichen und reellen Zahlen nicht geben kann, liegt letztlich darin begründet, dass jede reelle Zahl unendlich viel Information aufnehmen kann (man denke nur an Chaitins \( \Omega \) aus Kapitel 3.4), wärend natürliche Zahlen nur sehr wenig Information tragen. Die Vielfalt unendlicher Informationsspeicher lässt sich nicht durchnummerieren.
Eine spannende Frage lautet, ob es eine Menge gibt, die in ihrer Mächtigkeit zwischen den natürlichen Zahlen und den reellen Zahlen (die man auch als Kontinuum bezeichnet) gibt. Gibt es eine Menge, die sich nicht komplett durchnummerieren lässt, die sich aber auch nicht eins-zu-eins den reellen Zahlen zuordnen lässt, ohne dass reelle Zahlen übrig bleiben?
Es gelang Cantor nicht, eine solche Menge zu konstruieren. Daher formulierte er im Jahr 1878 seine berühmte Kontinuumshypothese:
Allerdings gelang es Cantor ebensowenig, diese Hypothese zu beweisen. Wir wissen heute, warum ihm dies nicht gelingen konnte. Auf Details gehen wir in einem späteren Kapitel noch genau ein.
Wir wollen uns ansehen, wie man den Mengenbegriff dazu verwenden kann, um ein möglichst tragfähiges Fundament für die Mathematik aufzubauen. Dabei lassen wir uns von Cantors Anschauung leiten, dass eine Menge einfach eine Ansammlung irgendwelcher Objekte ist, die wir Elemente der Menge nennen wollen.
Eine Menge ist dadurch festgelegt, dass wir angeben, welche Elemente sie enthält. Man schreibt auch \[ x \in A \] und meint damit, dass das Objekt \(x\) ein Element von \(A\) ist, also zur Menge \(A\) gehört. Wenn zwei Mengen dieselben Elemente enthalten, so bezeichnen wir die beiden Mengen als gleich oder identisch. Dabei ist die Reihenfolge der Elemente in der Menge egal (insofern unterscheidet sich eine Menge von einer geordneten Liste), und doppelt vorkommende Elemente spielen keine Rolle (Hauptsache, ein Exemplar ist in der Menge enthalten).
Mengen dürfen unendlich viele Elemente enthalten, oder auch gar keines. Die Menge ohne Elemente bezeichnen wir als leere Menge – wir wollen für sie das Symbol \( \varnothing \) verwenden.
Bleibt die Frage, welche Objekte in unserer mathematischen Welt vorkommen können. Cantor hatte noch etwas unscharf von bestimmten wohlunterschiedenen Objekten unserer Anschauung gesprochen. Wenn wir jedoch die Mengenlehre als Fundament für die Mathematik verwenden wollen, dann sollten wir mit möglichst wenigen irgendwie von außen kommenden Objekten auskommen. Schaffen wir es vielleicht sogar, ganz auf solche Objekte zu verzichten?
Wenn wir ganz auf andere Objekte verzichten wollen, so sind Mengen selbst die einzigen Objekte in unserer mathematischen Welt. Wir müssen es also zulassen, dass Mengen selbst Element von anderen Mengen sind. Das entspricht der Anschauung, dass man mehrere kleine Gruppen von Objekten zu einer großen Gruppe von Objekten zusammenfassen kann.
Versuchen wir also, eine Welt aufzubauen, die nur aus Mengen besteht. Mengen in dieser Welt bestehen wiederum aus Mengen, die auch wieder aus Mengen bestehen können und so fort. Wenn diese Kette irgendwo enden soll, so muss irgendwann eine Menge kommen, die keine weiteren Mengen als Elemente enthält. Eine solche Menge haben wir oben ausdrücklich erlaubt: die leere Menge (abgekürzt: \( \varnothing \) ). Diese leere Menge muss also den Ausgangspunkt für den Aufbau anderer Mengen bilden.
Beginnen wir also mit der leeren Menge \( \varnothing \) . Sie ist zunächst unser einziges Objekt, das wir als Element für eine Menge verwenden können. Die einzige Menge, die wir mit \( \varnothing \) aufbauen können, ist die Menge \( \{ \varnothing \} \), also die Menge, die die leere Menge \( \varnothing \) als Element enthält. Zur Notation: wenn wir eine Menge explizit durch Auflistung ihrer Elemente (sagen wir, \(a, b, c, ... \) ) angeben wollen, so schreiben wir diese Menge als \( \{ a, b, c, ... \} \), also mit geschweiften Klammern, in denen die Elemente aufgelistet sind. Die leere Menge \( \varnothing \) wird daher auch oft als \( \{ \} \) geschrieben. Die Menge \( \{ \varnothing , \varnothing \} \) ist übrigens gleich der Menge \( \{ \varnothing \} \), denn wir hatten oben gesagt, dass zwei Mengen gleich sind, wenn sie dieselben Elemente enthalten, wobei egal ist, wie oft ein Element aufgelistet ist. Die Anzahl Wiederholungen ist kein relevanter Begriff für eine Menge. Einzig relevant ist die Aussage, ob eine Menge ein Element enthält oder nicht. Dies hat den Vorteil, dass der Begriff des Zählens in der Mengenlehre nicht vorausgesetzt werden muss, sondern konstruiert werden kann, wie wir gleich sehen werden.
Wir sind also nun bereits im Besitz zweier verschiedener Objekte (Mengen), nämlich die leere Menge \( \varnothing \) und die Menge \( \{ \varnothing \} \), die die leere Menge als Element enthält. Diese beiden Objekte können wir nun als Elemente in einer neuen Menge verwenden: \( \{ \varnothing, \{ \varnothing \} \} \) . Und so können wir immer weiter machen, und immer neue Mengen nach diesem Schema konstruieren:
In jeder Stufe werden einfach alle bis dahin konstruierten Mengen als Elemente einer neuen Menge verwendet. Auf diese Weise erhalten wir unendlich viele verschiedene Mengen, ohne dass wir am Anfang irgendwelche Objekte vorausgesetzt haben. Die Mengenlehre zieht sich wie der Baron Münchhausen an den eigenen Haaren aus dem Sumpf.
Jede dieser Mengen enthält eine unterschiedliche Anzahl Elemente, und mit jeder Stufe kommt ein Element hinzu. In diesem Sinn bildet der schrittweise Aufbau neuer Mengen den Vorgang des Zählens nach. Die Idee liegt nahe, die Zahl \(0\) mit der Menge \( \varnothing \) zu identifizieren, die Zahl \(1\) mit der Menge \( \{ \varnothing \} \) und so fort, entsprechend der Anzahl Elemente in der jeweiligen Menge. Wir werden sehen, ob sich daraus ein Axiomensystem für die natürlichen Zahlen entwickeln lässt.
Nachdem wir bisher eine Reihe intuitiver Ideen gesammelt haben, müssen wir zur Präzisierung unserer Ideen ein konkretes formales Axiomensystem mit einer entsprechenden Sprache und zugehörigen Syntaxregeln aufzubauen. Schauen wir uns an, was für Zutaten wir dazu benötigen:
Wir brauchen keine weiteren Sprachelemente wie Konstanten oder Funktionen. Die Hoffnung ist, dass wir solche Sprachelemente später konstruieren können, ohne sie als elementare Bausteine voraussetzen zu müssen.
Mit diesen Sprachelementen können wir nun Aussagen aufbauen wie \( \forall y : \, \neg (y \in x) \), was soviel bedeutet wie, dass die Menge \(x\) keine Elemente enthält (also gleich der leeren Menge ist). Die Frage, die sich dabei unmittelbar stellt, lautet: Was ist der erlaubte Wertebereich für die Variablen \(x, y, z, ... \) der Theorie? Was bedeutet also die Aussage \( \forall y : \, ... \) ? Was sind das für \(y\) ?
Die intuitive Antwort, die wir aufgrund der obigen Überlegungen geben würden, lautet: Der erlaubte Wertebereich für die Variablen sind alle denkbaren Mengen, denn Mengen sind die einzigen Objekte in unserer Welt aus Mengen.
Damit haben wir nun das Vokabular sowie erste Syntaxregeln (die der klassichen Logik) der formalen Sprache der Mengenlehre festgelegt. Weitere Regeln und Axiome müssen nun hinzukommen, denn wir dürfen ja nicht einfach von einer bestimmten Bedeutung der Symbole ausgehen, sondern wir müssen die Syntaxregeln und Axiome so wählen, dass sie zur beabsichtigten Bedeutung der Symbole passen und damit diese Bedeutung für die Symbole nahelegen.
Als erstes wollen wir die Bedeutung des Gleichheitszeichens durch folgendes Axiom festlegen (man nennt dieses Axiom auch Extensionalitätsaxiom):
Wenn also alle Elemente, die in der Menge \(x\) sind, auch in der Menge \(y\) sind und umgekehrt, dann sind die beiden Mengen \(x\) und \(y\) gleich.
Der nächste Schritt besteht darin, neue Mengen konstruieren zu können. Dies geschieht dadurch, dass man alle Mengen, die eine gewisse Eigenschaft besitzen, zu einer neuen Menge zusammenfasst, wobei jede denkbare Eigenschaft eine entsprechende Menge zur Folge hat. Das folgende Axiom präzisiert diese Idee:
Dabei ist \(F(y)\) irgendein wohlgeformter Ausdruck in der formalen Sprache der Mengenlehre, die wir gerade definieren. Er repräsentiert gewissermaßen eine bestimmte Eigenschaft der Menge \(y\). Der Ausdruck \(F(y)\) enthält eine freie Variable \(y\), die nicht durch einen logischen Quantifier ( \( \forall y \) oder \( \exists y \) ) gebunden ist. Dagegen darf \(F(y)\) auf keinen Fall die Variable \(x\) enthalten.
Die Bedeutung dieses Axioms liegt darin, dass man alle Objekte \(y\), für die die Aussage \(F(y)\) gilt, zur Menge \(x\) zusammenfassen kann. Das Axiom fordert die Existenz einer entsprechenden Menge! In der Mathematik schreibt man eine solche Menge auch oft in der Form \( x = \{ y: F(y) \} \) , also die Menge aller \(y\), für die \( F(y) \) gilt.
Genau genommen handelt es sich bei dem obigen Axiom nicht um ein einziges Axiom, sondern um ein Axiomenschema, denn für jeden wohlgeformten Ausdruck \( F(y) \) gibt es ein solches Axiom (wir kennen das von dem Induktionsaxiom der Peano-Arithmetik). Bei Verwendung der Logik erster Ordnung ist es nicht erlaubt, diesem Axiomenschema den String \( \forall F(y) : \, ... \) voranzustellen, denn der logische Quantifier \( \forall \) darf nur für die Variablen der Theorie verwendet werden (ansonsten arbeitet man mit Logik zweiter Ordnung, die aber nicht axiomatisierbar ist – wir kommen in einem späteren Kapitel darauf zurück).
Das Komprehensions-Axiomenschema sieht vollkommen harmlos aus. Es entspricht unserer Intuition, dass man alle Objekte, denen man eine gewisse Eigenschaft zuschreiben kann, zu einer Menge zusammenfassen kann. Wir werden aber bald sehen, dass diese intuitive Vorstellung zu Problemen führen wird. Die Ursache für diese Probleme liegt darin, dass man versucht, einfach alle \(y\) unserer gedanklichen Mengenwelt aufzusammeln, für die \( F(y) \) gilt. Dabei wird etwas zuviel aufgesammelt, denn nicht jede Menge eignet sich als Element einer weiteren Menge! Details folgen etwas weiter unten.
Mit Hilfe des Komprehensions-Axiomenschemas sind wir in der Lage,
die Existenz der leeren Menge \( \varnothing \) zu beweisen. Dazu verwenden wir für \( F(y) \)
den Ausdruck \( \neg (y=y) \), der immer falsch ist. Das Axiom liefert dann
\[
\exists x: \forall y : \, [ (y \in x) \iff \neg (y=y) ]
\]
Da \( \neg (y=y) \) für kein \(y\) gelten kann, ermöglichen es die Regeln der Logik,
diesen Ausdruck umzuwandeln in
\[
\exists x: \forall y : \, [ \neg (y \in x) ]
\]
Es gibt also eine Menge \(x\), die keine Elemente enthält. Dies ist genau die leere Menge \( \varnothing \).
Damit haben wir bereits fast alle Axiome beisammen, die Cantors intuitiver Mengenlehre zugrundeliegen. Ein Axiom fehlt dabei noch: das Auswahlaxiom (wobei Cantor dieses Axiom nie explizit ausgesprochen, sondern nur intuitiv verwendet hat). Dieses Axiom sagt, dass man aus jeder Menge ein Element auswählen kann, wobei das Axiom nicht verrät, wie das gehen soll. Wir sind auf dieses Axiom bereits in Kapitel 3.2 eingegangen, und haben auf die Probleme hingewiesen, dieses Axiom anschaulich als wahr oder falsch zu interpretieren. Details folgen im nächsten Kapitel.
Wie mächtig ist nun dieses extrem einfache Axiomensystem, das gerade einmal die Axiome der Logik, Variablen, zwei Prädikate ( \( \in \) und \( = \) ) und drei Axiome enthält: das Extensionalitäts-Axiom zur Definition der Gleichheit \( = \) , das Komprehensions-Axiomenschema zum Zusammenfassen von Elementen mit gleichen Eigenschaften, das die Bedeutung von \( \in \) festlegt, sowie das Auswahlaxiom zum Auswählen von Elementen aus Mengen, auf das wir im nächsten Kapitel eingehen.
Es zeigt sich, dass dieses Axiomensystem sogar sehr mächtig ist. Die gesamte bekannte Mathematik lässt sich aus ihm ableiten. Allerdings reichen die Axiome auch aus, um einen Widerspruch zu beweisen, und ein widerspruchsvolles formales System kann sowieso alles beweisen. Wir haben also die Beweiskraft des Systems zu weit getrieben!
Schauen wir uns an, wie der Widerspruch entsteht:
Anschaulich gehen wir im Normalfall davon aus, dass Mengen sich nicht selbst als Element enthalten. Allerdings werden Mengen, die sich selbst als Element enthalten, durch die Axiome auch nicht ausgeschlossen. Mengen (nennen wir sie \(y\) ), die sich nicht selbst als Element enthalten, werden durch den Ausdruck \( \neg (y \in y) \) charakterisiert. Dies ist ein wohlgeformter Ausdruck \(F(y)\) mit einer freien Variable \(y\), den wir nach unserem Komprehensions-Axiomenschema dazu verwenden können, um eine neue Menge \(x\) zu charakterisieren, die alle die Mengen als Elemente enthält, die sich selbst nicht als Elemente enthalten. Dazu setzen wir im Komprehensions-Axiomenschema einfach für \(F(y)\) den Ausdruck \( \neg (y \in y) \) ein: \[ \exists x: \forall y : \, [ (y \in x) \iff \neg (y \in y) ] \] Anschaulich ist die Menge \(x\) damit die Menge aller Mengen \(y\), die sich nicht selbst enthalten. Da die Aussage in der eckigen Klammer für alle \(y\) gilt, gilt sie auch für das spezielle \(y\), das gleich \(x\) ist. Wir können den obigen Ausdruck gemäß den Regeln der Logik also umformen in den Ausdruck \[ \exists x: \, [ (x \in x) \iff \neg (x \in x) ] \] Und das ist ein klarer Widerspruch, denn die Aussage \( (x \in x) \) steht der Aussage \( \neg (x \in x) \) gegenüber. Man kann nicht entscheiden, ob die Menge, die alle die Mengen enthält, die sich nicht selbst enthalten, sich selbst nun enthält oder nicht. Dieser Widerspruch ist ganz analog zu dem bekannten Paradoxon des Barbiers, der alle die Menschen rasiert, die sich nicht selbst rasieren. Rasiert sich dieser Barbier nun selbst oder nicht?
Das Komprehensions-Axiomenschema hat vollkommen unerwartet zu einem Widerspruch geführt. Auf die Frage "Enthält die Menge aller Mengen, die sich nicht selbst enthalten, denn sich selbst?" gibt es keine Antwort. Die Menge \(x\) enthält sich genau dann selbst, wenn sie sich nicht enthält.
Dieser Widerspruch wurde im Jahr 1901 von Bertrand Russel entdeckt, allerdings nicht direkt in Cantors Mengenlehre, sondern in Freges formalem mathematischen System. Der Widerspruch lässt sich aber wie gerade gesehen unmittelbar auf Cantors Mengenlehre übertragen und wird dort auch als Russels Paradoxon oder Russellsche Antinomie bezeichnet.
Eine kurze Nebenbemerkung: Die Entdeckung von Widersprüchen lief historisch im Detail komplizierter ab, als hier dargestellt. Cantor selbst entdeckte bereits im Jahr 1895 einen ersten Widerspruch in seiner Mengenlehre.
Für Cantor, Frege und andere war die Entdeckung von Widersprüchen in ihren mathematischen Systemen ein schwerer Schlag, der ihr Lebenswerk zu zerstören schien. Der erste Versuch, die bekannte Mathematik in einem formalen Axiomensystem zu erfassen, war gescheitert.
Niemand hatte solche Widersprüche erwartet! Die Axiome sahen vollkommen gesund aus. Sie erscheinen intuitiv einleuchtend und wahr zu sein. Dies zeigt, dass man niemals vor Widersprüchen sicher sein kann, und leider kann man nach Gödels zweitem Satz auch nie innerhalb eines formalen Systems dessen Widerspruchsfreiheit beweisen. Es gibt keine Garantie, die einen vor Widersprüchen absolut sicher schützt.
Andererseits kann man fast die gesamte Mathematik auf die Mengenlehre zurückführen. Die Begriffe und Ideen der Mengenlehre scheinen also durchaus nützlich zu sein, wenn nur die Widersprüche nicht wären. Es liegt also nahe, zu versuchen, die Axiome der Mengenlehre so zu verändern, dass die Widersprüche verschwinden, ohne dass die Aussagekraft des Systems zu stark eingeschränkt wird.
Eine der entscheidenden Ideen dazu stammt von Ernst Zermelo aus dem Jahr 1908. Zermelo untersuchte die Ursache für Russels Widerspruch. Wie wir oben gesehen haben, liegt die Ursache darin, dass das Komprehensions-Axiomenschema es erlaubt, zu jedem Ausdruck \(F(y)\) mit einer freien Variablen eine entsprechende Menge zu konstruieren, die alle Mengen \(y\) enthält, für die \(F(y)\) gilt. Dieses Axiom ist offenbar zu allgemein, denn es führt für \(F(y)\) gleich \( \neg (y \in y) \) zu einem Widerspruch. Aber wie lässt sich das Axiom geeignet einschränken, so dass der Widerspruch nicht mehr konstruierbar ist, ohne dass die Kraft des Axioms zu stark eingeschränkt wird?
Die Kernidee liegt darin, zu erkennen, dass man nicht beliebige Mengen zur Bildung einer neuen Menge verwenden darf. Nicht jede denkbare Menge, für die eine Aussage \(F(y)\) gilt, darf man als Element einer neuen Menge verwenden. Welche Mengen darf man aber zu einer neuen Menge aufsammeln?
Die Lösung lautet: Man darf nur solche Mengen zur Bildung einer neuen Menge über eine Aussage \(F(y)\) verwenden, die selbst Element einer anderen Menge sind. Nicht jede denkbare Menge \(y\) mit der Eigenschaft \(F(y)\) darf also als Element einer neuen Menge \(x\) verwendet werden, sondern nur diejenigen \(y\), die Element einer anderen Menge \(z\) sind. Das entsprechend abgeänderte Axiom lautet:
Wenn wir dieses Axiom mit dem ursprünglichen Komprehensions-Axiom \[ \exists x: \forall y : \, [ (y \in x) \iff F(y) ] \] vergleichen, dann sehen wir, dass einfach zwei Teile hinzugekommen sind: Am Anfang wurde \( \forall z : \, ... \) vorangestellt, und weiter hinten wurde der Teil \( (y \in z) \land \, ... \) eingefügt. Damit ist gesichert, dass die \(y\), die zur Bildung der neuen Menge \(x\) über die Eigenschaft \(F(y)\) verwendet werden, bereits Element einer anderen Menge \(z\) sein müssen. Es werden also alle Elemente von \(z\), die eine bestimmte Eigenschaft haben, herausgesucht und zu einer neuen Menge \(x\) zusammengefasst. Damit muss die neue Menge \(x\) immer Untermenge einer bereits bestehenden Menge \(z\) sein.
Was geschieht nun, wenn wir erneut versuchen, für \(F(y)\) die Aussage \( \neg (y \in y) \) einzusetzen? Lässt sich dadurch immer noch ein Widerspruch ableiten? Versuchen wir es: \[ \forall z : \exists x: \forall y : \, [ (y \in x) \iff ( (y \in z) \land (\neg (y \in y)) ) ] \] Das bedeutet: Nur die Mengen \(y\), die sich nicht selbst enthalten (sodass rechts \( (\neg (y \in y)) \) wahr ist) und die Element irgendeiner Menge \(z\) sind (sodass rechts \( (y \in z) \) wahr ist), können zu einer Menge \(x\) zusammengefasst werden, sodass links \( (y \in x) \) wahr ist.
Nun streichen wir wieder \( \forall y \) heraus, indem wir für \(y\) überall den konkreten Wert \(x\) einsetzen: \[ \forall z : \exists x: \, [ (x \in x) \iff ( (x \in z) \land (\neg (x \in x)) ) ] \] Liegt hier immer noch ein Widerspruch vor?
Schauen wir uns an, was geschieht, wenn wir annehmen, es gäbe ein \( x \), das sich selbst enthält, sodass \( (x \in x) \) wahr ist. Dann muss auch die Aussage rechts von \( \iff \) (das genau dann wenn bedeutet) wahr sein, also muss \( (x \in z) \land (\neg (x \in x)) \) wahr sein. Da aber \( \neg (x \in x) \) nach Annahme falsch ist ( \(x\) soll sich ja selbst enthalten) und damit der ganze Ausdruck \( (x \in z) \land (\neg (x \in x)) \) ebenfalls falsch ist, haben wir einen Widerspruch. Also muss die Annahme, es gäbe ein \( x \), dass sich selbst enthält, falsch sein, d.h. ein solches \(x\) gibt es nicht. Keine Menge \(x\) kann sich selbst enthalten.
Also muss \( (x \in x) \) falsch und \( \neg (x \in x) \) wahr sein für alle Mengen \(x\). Da \( (x \in x) \) falsch ist und auf der linken Seite von \( \iff \) steht, muss auch der Ausdruck \( (x \in z) \land (\neg (x \in x)) \) rechts von \( \iff \) falsch sein. Darin ist aber der Teil \( \neg (x \in x) \) wahr, sodass der andere Teil \( (x \in z) \) falsch sein muss für alle Mengen \(z\). Dieser andere Teil \( (x \in z) \) rechts rettet die ganze Situation und verhindert den Widerspruch, indem er die "Falschheit" rechts absorbiert. Gäbe es ihn nicht, so müsste \( \neg (x \in x) \) rechts falsch sein, was zum Widerspruch führt.
Das Axiom sagt also, dass es eine Menge \(x\) gibt ( \( \exists x: \) ), die genau dann, wenn sie sich nicht selbst enthält (was immer stimmt), zugleich auch in keiner anderen Menge \(z\) enthalten ist. Es gibt also eine Menge \(x\), die in keiner anderen Menge \(z\) enthalten ist. Ein Widerspruch bleibt aus.
Die Existenz einer solchen Menge \(x\) verhindert, dass man die Menge aller Mengen bilden kann, denn eine dieser Mengen (nämlich \(x\) ) darf nicht in einer anderen Menge vorkommen. Genau dadurch wird die Entstehung von Russels Paradoxie vermieden, und man ist bisher auf keine weiteren Widersprüche gestoßen.
Man zahlt allerdings einen Preis dafür, dass man das Komprehensions-Axiom so eingeschränkt hat, dass nur Elemente von bestehenden Mengen zu neuen Mengen zusammengefasst werden können, denn es wird nun schwieriger, neue Mengen zu bilden. Es reicht nicht mehr aus, einfach eine Aussage \(F(y)\) vorzugeben, um eine Menge zu konstruieren, denn jede so konstruierte Menge ist nach dem Aussonderungsaxiom lediglich eine Untermenge zu einer bereits bestehenden Menge. Daher sind weitere Axiome notwendig, um die Konstruktion neuer, größerer Mengen zu erlauben. Das heute am meisten verwendete Axiomensystem dieser Art trägt den Namen Zermelo-Fränkel-Axiomensystem (oft abgekürzt als ZF oder ZFC, wenn man das Auswahlaxiom C (also Choice) mit hinzunimmt). Wir werden uns dieses System im nächsten Kapitel im Detail ansehen und einen Eindruck davon bekommen, wie man Schritt für Schritt die gesamte klassische Mathematik in diesem System ausdrücken kann. Und schließlich wollen wir uns im darauf folgenden Kapitel auch die Grenzen dieses extrem mächtigen formalen Systems ansehen, wenn wir uns mit der Kontinuumshypothese befassen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 06 March 2023