Von Trägheit und Schwung zu Masse und Impuls
Impulserhaltung und Relativitätsprinzip
Der nichtrelativistische Impuls
Impuls und Trägheit in der Relativitätstheorie
Auch Felder besitzen Trägheit und Impuls
Die beiden Begriffe Masse und Impuls sind uns im letzten Kapitel bereits begegnet, denn sie sind untrennbar mit dem Kraftbegriff verbunden. Isac Newton hatte es als Erster erkannt: Wirkt eine Kraft auf einen Körper, so ändert sich dessen Bewegung (Aktionsprinzip), während ohne Krafteinwirkung die Bewegung des Körpers geradlinig-gleichförmig oder ruhend bleibt (Trägheitsprinzip). Präzise ausgedrückt bedeutet das, dass die zeitliche Änderung des Impulses gleich der wirkenden Kraft ist: \begin{equation} \boldsymbol{F} = \frac {d \boldsymbol{p} }{dt} \end{equation} Hinzu kommt das Wechselwirkungsprinzip, nach dem innere Kräfte (beispielsweise zwischen zwei Sternen in einem Doppelsternsystem) den Gesamtimpuls des Systems nicht ändern (Impulserhaltung).
Man könnte die Formel \( \boldsymbol{F} = d \boldsymbol{p}/dt \) für eine reine Definition halten, doch damit wäre überhaupt nichts gewonnen, wie wir im letzten Kapitel bereits gesehen haben. Wir müssen der Formel vielmehr physikalisches Leben einhauchen, indem wir einerseits mehr über die Kräfte herausfinden, die in der Natur zwischen verschiedenen Objekten wirken, und indem wir andererseits den Impuls in Bezug zur Bewegung des Objekts setzen – letzteres soll Thema dieses Kapitels sein: Wieviel Impuls hat ein Körper, der sich mit einer bestimmten Geschwindigkeit \( \boldsymbol{v} \) bewegt?
Die entsprechenden Formeln sind im letzten Kapitel gewissermaßen vom Himmel gefallen: Der Impuls ist gleich der Masse mal der Geschwindigkeit des Körpers, also \( \boldsymbol{p} = m \boldsymbol{v} \) – so lernt man es in der Schule. Doch warum ist das so? Muss das so sein? Keineswegs muss das so sein, wie wir bereits gesehen haben, denn die Trägheit eines Körpers nimmt in Wirklichkeit zu, wenn er schneller wird, sodass ein Korrekurfaktor \( \gamma \) (der Lorentzfaktor) hinzukommt: \( \boldsymbol{p} = m \gamma \boldsymbol{v} \). Diese Zunahme der Trägheit macht sich allerdings erst bei sehr großen Geschwindigkeiten bemerkbar, die in der Nähe der Lichtgeschwindigkeit liegen. Für kleine Geschwindigkeiten ist daher \( \gamma \) kaum größer als 1, während in Richtung Lichtgeschwindigkeit \( \gamma \) und damit die Trägheit gegen Unendlich strebt.
Wie Impuls und Geschwindigkeit zusammenhängen, ist natürlich letztlich eine experimentelle Frage, denn was immer wir uns auch ausdenken – es muss Vorhersagen über die Bewegung von Körpern ermöglichen, die mit der Realität übereinstimmen. Also könnte man sagen: Zusammen mit dem Lorentzfaktor haben wir die richtige Impulsformel gefunden, denn sie wird durch das Experiment bestätigt. Doch irgendwie ist das unbefriedigend: Wir wollen verstehen, welche Grundprinzipien zu diesem Gesetz führen. Wo kommen diese Formeln letztlich her?
Es gibt tatsächlich ein Grundprinzip, das uns hier weiterhilft: Das Relativitätsprinzip, das wir bereits in den beiden Kapiteln zu Raum und Zeit kennengelernt haben. Es besagt, dass die Natur in jedem sich gleichförmig bewegenden Bezugssystem (Inertialsystem) durch dieselben Naturgesetze beschrieben wird (zumindest wenn wir die Komplikationen durch Einsteins Gravitationstheorie außen vor lassen). Befindet man sich beispielsweise in einem gleichmäßig dahinfliegenden Raumschiff und sieht ein anderes Raumschiff vorbeigleiten, so kann man nicht sagen, welches Raumschiff ruht und welches sich bewegt. Innerhalb jedes der beiden Raumschiffe merkt man von einer gleichförmigen Eigenbewegung des Raumschiffs rein gar nichts. Es könnte genauso gut stillstehen.
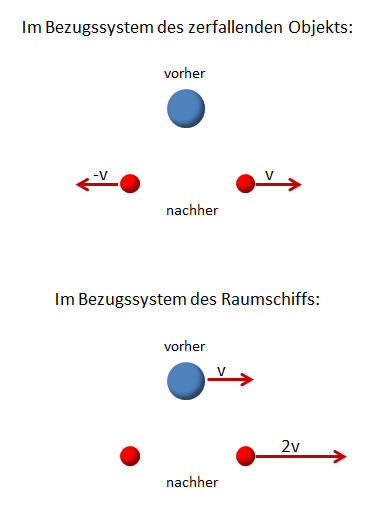
Wie kann uns dieses Prinzip weiterhelfen? Schauen wir uns dazu irgendein ruhendes Objekt im leeren Weltraum an, das in zwei gleichartige Objekte auseinanderfällt, die anschließend in entgegengesetzte Richtungen wegfliegen. Es könnte sich bei dem ruhenden Objekt beispielsweise um zwei kleine identische Metallkugeln handeln, die zunächst irgendwie miteinander verriegelt sind und die sich außerdem gegenseitig abstoßen. Sobald die Verriegelung gelöst wird, fliegen sie auseinander. Oder aber es könnte sich aber um irgendein Elementarteilchen handeln, das spontan in zwei andere einander gleiche Teilchen zerfällt. Wir brauchen hier nicht zu wissen, um was für ein Objekt es sich handelt. Alles was wir brauchen ist die Tatsache, dass wir zunächst ein ruhendes Objekt vor uns haben, aus dem irgendwie zwei andere einander gleiche Objekte werden, die auseinanderfliegen.
Wie muss nun eine Größe aussehen, die eine Art inneren Schwung dieser Objekte repräsentiert – genau das soll der Impuls ja darstellen? Wir erwarten, dass dieser Schwung umso größer ist, je schneller das Objekt ist. Und noch eine zweite Erfahrung lassen wir einfließen: Wir erwarten, dass der Schwung umso größer ist, je massiver bzw. träger ein Objekt ist, d.h. je weniger gut es sich bei gleicher Kraftwirkung aus seiner Bahn ablenken lässt. Mit diesen Annahmen lassen wir gewissermaßen unsere experimentellen Beobachtungen zur Physik bewegter Objekte einfließen, denn nur so können wir einen geeigneten physikalischen Startpunkt zur Begriffsbildung finden.
Unser betrachtetes Startobjekt von oben sollte also gar keinen Schwung bzw. Impuls besitzen, denn es bewegt sich ja nicht. Nach dem Auseinanderfallen erwarten wir, dass die beiden entandenen Einzelobjekte genau mit derselben Geschwindigkeit \( \boldsymbol{v} \) in entgegengesetzte Richtungen auseinanderfliegen, denn sie sind einander vollkommen gleichwertig, sodass es keine Bevorzugung für eines der beiden Objekte geben sollte. Tatsächlich bestätigt das Experiment diese Erwartung: die beiden Objekte fliegen wirklich mit entgegengesetzt-gleichen Geschwindigkeiten \( \boldsymbol{v} \) und \( -\boldsymbol{v} \) auseinander. Nach Newtons Wechselwirkungsprinzip muss es auch so sein, wenn wir beispielsweise die beiden Metallkugeln betrachten, die durch eine Abstoßungskraft zwischen den beiden Kugeln auseinandergetrieben werden, sodass der Gesamtimpuls erhalten bleiben muss. Vor dem Auseinanderfallen ist der Impuls Null, und er muss es auch nachher noch sein, d.h. die beiden Impulse der auseinanderfliegenden Objekte müssen entgegengesetzt gleich sein.
Wir wollen nun davon ausgehen, dass wenn das Gesetz der Impulserhaltung in irgendeinem Inertialsystem (gleichförmig bewegtem oder ruhendem Bezugssystem) gilt, dass es dann auch in allen anderen Inertialsystemen gilt, die sich relativ dazu geradlinig-gleichförmig bewegen. Genau so muss es sein, wenn die Impulserhaltung ein Naturgesetz ist und wenn wir das Relativitätsprinzip voraussetzen, nach dem ein Naturgesetz in allen Inertialsystemen gelten muss. Wir können uns dieselbe Situation also auch aus einem gleichmäßig dahingleitenden Raumschiff heraus ansehen. Seine Geschwindigkeit soll so gewählt sein, das das linke der beiden auseinanderfliegende Objekte vom Raumschiff aus gesehen ruht.
Wir erwarten nun, dass wir folgendes sehen:
Vor dem Zerfall bewegt sich das ursprüngliche Objekt mit der Geschwindigkeit \( \boldsymbol{v} \),
denn wir selbst bewegen uns ja nun mit der Geschwindigkeit \( -\boldsymbol{v} \)
relativ zu diesem Objekt.
Nach dem Zerfall ruht das linke neu entstandene Objekt, während das rechte Objekt
sich mit der Geschwindigkeit \( 2\boldsymbol{v} \) bewegt – unser Raumschiff bewegt sich ja
mit \( -\boldsymbol{v} \) in die Gegenrichtung.

Die Trägheit der Objekte wollen wir nun durch eine Masse charakterisieren, die für jedes Objekt charakteristisch und unveränderlich sein soll. Falls die Trägheit mit zunehmender Geschwindigkeit größer werden sollte, so wollen wir dies ggf. durch einen Korrekturfaktor berücksichtigen, sodass sich die Masse selbst nicht ändert. Die Masse stellt also die Trägheit eines noch ruhenden Objekts dar, sodass man auch von der Ruhemasse spricht.
Die Masse der beiden auseinanderfliegenden Objekte soll jeweils \( m \) sein, die Masse des Objektes vor dem Zerfall soll \( M \) sein. Wenn wir nun für alle Impulse den Ansatz Impuls gleich Masse mal Geschwindigkeit machen, so passt alles wunderbar zusammen: Der Impuls ist wie verlangt umso größer, je massiver (träger) und je schneller ein Objekt ist, und außerdem gilt die Impulserhaltung in beiden Bezugssystemen. Hier die Begründung:
Bei ruhendem Anfangsobjekt ist vor dem Zerfall der Impuls \( \boldsymbol{P} = 0 \) und nach dem Zerfall haben wir die beiden Impulse \( \boldsymbol{p}_1 = - m \boldsymbol{v} \) und \( \boldsymbol{p}_2 = m \boldsymbol{v} \) , die sich zu Null aufaddieren, sodass die Impulserhaltung \( \boldsymbol{P} = \boldsymbol{p}_1 + \boldsymbol{p}_2 \) erfüllt ist.
Aus dem Raumschiff betrachtet ist vor dem Zerfall der Impuls \( \boldsymbol{P} = M \boldsymbol{v} \) und nach dem Zerfall haben wir die beiden Impulse \( \boldsymbol{p}_1 = 0 \) und \( \boldsymbol{p}_2 = 2 m \boldsymbol{v} \). Auch hier gilt die Impulserhaltung \( \boldsymbol{P} = \boldsymbol{p}_1 + \boldsymbol{p}_2 \), wenn wir eines voraussetzen: Die Masse \(M\) des zerfallenden Objekts muss gleich der Massensumme der beiden daraus entstehenden Objekte sein: \( M = 2 m \). Massen müssen also additiv sein, damit hier die Impulserhaltung gilt! Das erscheint uns selbstverständlich zu sein, aber es ergibt sich auch zwangsläufig aus unseren Überlegungen. Weiter unten werden wir jedoch sehen, dass diese scheinbare Selbstverständlichkeit gar nicht selbstverständlich ist: Bei großen Geschwindigkeiten ist sie sogar falsch!
Natürlich ist das alles noch kein vollständiger Beweis dafür, dass "Impuls gleich Masse mal Geschwindigkeit" sein muss, aber es zeigt, wie gut dieser Ansatz zu unseren Voraussetzungen Impulserhaltung und Relativitätsprinzip passt. Und dennoch sollten wir an dieser Stelle stutzig werden: Hatten wir nicht gesagt, dass genau genommen noch ein Korrekturfaktor \( \gamma \) auftauchen sollte, der bei größeren Geschwindigkeiten zum Tragen kommt? Aber wie um Himmels Willen passt das zu unserer obigen Überlegung, in der dieser Faktor gar nicht notwendig war? Irgendwo haben wir bei unserer Überlegung eine Zusatzannahme hineingesteckt, die nicht haltbar ist, wenn wir sie experimentell überprüfen.
Wir werden sehen, dass es die Geschwindigkeit der wegfliegenden Kugel ist, die wir aus dem Raumschiff heraus sehen. Wie selbstverständlich haben wir angenommen, dass die mit \( \boldsymbol{v} \) fliegende Kugel aus dem mit \( -\boldsymbol{v} \) fliegenden Raumschiff betrachtet so aussieht, als flöge sie mit \( 2\boldsymbol{v} \). Bei Geschwindigkeiten deutlich unterhalb der Lichtgeschwindigkeit stimmt das auch recht gut. Ein sorgfältiges Experiment würde aber zeigen, dass diese Annahme nicht genau stimmt, wobei der Fehler erst bei sehr großen Geschwindigkeiten auffällt. Wenn wir uns Einsteins Relativitätstheorie ins Gedächtis rufen, nach der nichts schneller als mit Lichtgeschwindigkeit fliegen kann, so wird unser Denkfehler sichtbar: Wäre \( \boldsymbol{v} \) beispielsweise 75 % der Lichtgeschwindigkeit, so würden wir vom Raumschiff aus die zweite Kugel mit 150 % der Lichtgeschwindigkeit – also mit Überlichtgeschwindigkeit – davonfliegen sehen. Das kann aber nach Einstein nicht sein, denn in jedem gleichförmig bewegten Bezugssystem bewegt sich nichts schneller als das Licht!
Wir müssen unsere obige Überlegung zum Impuls also überarbeiten und verallgemeinern, damit wir die richtigen Schlüsse daraus ziehen können. Dieser Abschnitt ist daher zwangsläufig etwas mathematischer orientiert – aber es lohnt sich!
Um das Relativitätsprinzip besser formulieren zu können, wollen wir zunächst eine allgemeine Beschreibung für den Wechsel zwischen gleichförmig bewegten Bezugssystemen (Inertialsystemen) aufstellen. Dazu ist es sehr nützlich, Raum und Zeit formal zu einer vierdimensionalen Raumzeit zusammenzufassen, wobei wir die Zeit \(t\) noch mit der Lichtgeschwindigkeit \(c\) multiplizieren, sodass sie ebenfalls die Dimension einer Länge erhält. Hermann Minkowski, den wir im letzten Kapitel schon kennengelernt haben, war seinerzeit auf diese geniale Idee gekommen! Ein Ereignis (also ein Punkt) in dieser Raumzeit wird nun also durch einen vierkomponentigen Vektor (Vierervektor) \begin{equation} x = \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} = \begin{pmatrix} c t \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} = \begin{pmatrix} c t \\ \boldsymbol{x} \end{pmatrix} \end{equation} dargestellt, dessen vier Komponenten \( x^\mu \) wir mit dem griechischen Index \( \mu \) von 0 bis 3 durchnummerieren wollen, wobei wir den Index oben schreiben statt unten (dies ist zumindest in der Relativitätstheorie so üblich). Dabei soll die nullte Komponente der Zeitpunkt des Ereignisses (mal der Lichtgeschwindigkeit \(c\) ) sein, also \( x^0 = c t \), während die anderen drei Komponenten zum räumlichen Vektor \begin{equation} \boldsymbol{x} = \begin{pmatrix} x^1 \\ x^2 \\ x^3 \end{pmatrix} \end{equation} gehören, der den Ort des Ereignisses kennzeichnet und den wir weiterhin durch Fettdruck kennzeichnen (den Vierervektor \(x\) schreiben wir dagegen ohne Fettdruck).
Wenn sich nun ein Objekt im Lauf der Zeit durch den Raum bewegt, so
beschreibt es dabei eine Bahnkurve
\( \boldsymbol{x}(t) \) im Raum.
Zu jedem Zeitpunkt \(t\) gehört dabei ein Ort \( \boldsymbol{x}(t) \),
an dem es sich zur Zeit \(t\) befindet.
In unserer vierdimensionalen Raumzeit
entsteht so ebenfalls eine Kurve (eine Bahn oder auch Weltlinie), die durch die Vierervektoren
\begin{equation}
\begin{pmatrix}
c t \\
\boldsymbol{x}(t)
\end{pmatrix}
\end{equation}
charakterisiert ist.
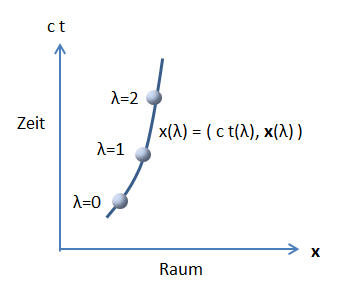
Hier haben wir nun aber die Möglichkeit, an Stelle der Zeit \(t\)
irgendeinen anderen Kurvenparameter \( \lambda \) zu verwenden, mit dem
wir nacheinander alle Raumzeitpunkte der Kurve abfahren können:
\begin{equation}
x(\lambda) =
\begin{pmatrix}
c t(\lambda) \\
\boldsymbol{x}(\lambda)
\end{pmatrix}
\end{equation}
Genau genommen hätten wir
\( \boldsymbol{x}(t((\lambda)) \)
schreiben müssen,
denn für die einzelnen \( \lambda \)-Werte ergeben sich natürlich wieder die verschiedenen
Zeitwerte und die zugehörigen Orte auf der Bahnkurve.
Ich möchte hier aber nicht zu aufwändige Bezeichnungsweisen einführen.
Der Ort \( \boldsymbol{x}(\lambda) \) ist also als der Ort zu verstehen, an dem sich das Objekt
zur Zeit \( t(\lambda) \) befindet.
Wozu ist das nun gut? Es hilft, Zeit und Ort bei einem Bezugssystemwechsel in gleicher Weise sehr übersichtlich zu behandeln. Wenn wir nämlich dieselbe Bewegung aus einem dahingleitenden Raumschiff heraus betrachten, so verändert sich die Bahnkurve \( x(\lambda) \). Ein vormals ruhendes Objekt erscheint beispielsweise nun bewegt. Also wird man für die Bewegung vom Raumschiff aus gesehen andere Ortskoordinaten ermitteln, welche die Bewegung relativ zum Raumschiff beschreiben. Außerdem könnte es sein, dass die Uhr, die im Raumschiff verwendet wird, grundsätzlich nicht synchron mit einer außenstehenden Uhr läuft – es könnte sich also auch die Zeitkoordinate ändern, mit der man in verschiedenen Bezugssystemen die Zeitpunkte bezeichnet. Newton wäre das noch absurd erschienen, aber Einstein würde hier weise nicken. Vom Raumschiff aus gesehen wird die Bewegung also durch eine Bahnkurve \begin{equation} x'(\lambda) = \begin{pmatrix} c t'(\lambda) \\ \boldsymbol{x}'(\lambda) \end{pmatrix} \end{equation} in der Raumzeit beschrieben, ausgedrückt durch das mitgeführte Raumschiff-Koordinatensystem und die Zeit auf einer mitgeführte Raumschiff-Uhr, die wir beide durch einen kleinen Strich kennzeichnen.
Wie hängen nun die beiden Beschreibungen \( x(\lambda) \) und \( x'(\lambda) \) derselben Bewegung, gesehen aus den beiden verschiedenen Inertialsystemen, miteinander zusammen? Die Details schauen wir uns etwas später an; an dieser Stelle genügt zunächst eine ganz allgemeine Bemerkung: Eine kräftefreie, also geradlinig-gleichförmige Bewegung muss aus allen Inertialsystemen heraus geradlinig-gleichförmig aussehen, denn diese Bezugssysteme entsprechen ja Beobachtern, die sich relativ zueinander geradlinig-gleichförmig bewegen. Um beim Bezugsystemwechsel die neuen Raumzeit-Koordinaten aus den alten zu berechnen, darf man letztere daher zwar mit Zahlen multiplizieren und diese Produkte auch aufaddieren, aber man darf die Koordinaten beispielsweise nicht quadrieren. Mathematisch bedeutet das, dass die neuen Koordinaten aus den alten durch eine lineare Abbildung hervorgehen (Verschiebungen in Raum und Zeit lassen wir hier zur Vereinfachung weg, da wir ja nur die Nullpunkte passend wählen müssen).
Lineare Abbildungen lassen sich allgemein durch Matrizen darstellen. Die entsprechende Koordinaten-Transformationsmatrix wollen wir mit dem Buchstaben \( \Lambda; \) bezeichnen. Sie hat 4 Zeilen und 4 Spalten und enthält die Zahlen (Matrixelemente) \( \Lambda^\mu_{\;\nu} \) mit den Indices \(\mu\) und \(\nu\) von 0 bis 3. Die Indices sind hier oben und unten geschrieben analog zu den Konventionen in der Relativitätstheorie. Dabei steht \(\mu\) für die Zeilennummer und \(\nu\) für die Spaltennummer des Matrixelementes. Mit diesen Zahlen müssen die alten Koordinaten multipliziert und anschließend aufsummiert werden, um die neuen Koordinaten zu erhalten:
Kurzschreibweise: \begin{equation} x' = \Lambda x \end{equation} Bedeutung: \begin{equation} x'^\mu = \sum_{\nu = 0}^3 \Lambda^\mu_{\;\nu} x^\nu \end{equation} wobei \( \sum \) das Summenzeichen ist, also beispielsweise \begin{equation} x'^0 = \Lambda^0_{\;0} x^0 + \Lambda^0_{\;1} x^1 + \Lambda^0_{\;2} x^2 + + \Lambda^0_{\;3} x^3 \end{equation} Damit ist garantiert, dass eine geradlinig-gleichförmige Bewegung \( x(\lambda) \) aus dem anderen Bezugssystem heraus gesehen wieder eine geradlinig-gleichförmige Bewegung \( x'(\lambda) \) ergibt. Wie das in ganz konkreten Fällen aussieht, sehen wir weiter unten.
Eine allgemeine Bahnkurve \( x(\lambda) \) in der Raumzeit wird also nach dem Bezugssystemwechsel durch die Bahnkurve \begin{equation} x'(\lambda) = \Lambda x(\lambda) \end{equation} beschrieben. Der Kurvenparameter \( \lambda \) selbst ändert sich dabei nicht – genau darin liegt der Vorteil, wenn man nicht die Zeit als Kurvenparameter verwendet, denn diese könnte sich beim Bezugssystemwechsel ja verändern. Da wir die Zeit jedoch als nullte Koordinate der Bahnkurve in der Raumzeit mitführen, können wir ihre Veränderung ganz analog zur Veränderung der räumlichen Koordinaten behandeln.
Um einen weiteren Schritt in Richtung Impuls voranzukommen, brauchen wir
nun so etwas wie eine Geschwindigkeit. Wieder ist es sinnvoll, nicht
direkt die Geschwindigkeit
\( \boldsymbol{v} = d\boldsymbol{x}/dt \)
zu verwenden, denn diese ist die zeitliche Veränderungsrate des
Ortes und unterliegt damit wieder komplizierten Regeln, wenn sich die Zeit
beim Bezugssystemwechsel ändert. Statt dessen wollen wir die
Veränderungsrate
\begin{equation}
u^\mu(\lambda) = \frac {dx^\mu(\lambda)}{d\lambda}
\end{equation}
der vier Raumzeit-Kurvenkoordinaten mit anwachsendem Kurvenparameter \( \lambda \) betrachten,
denn \( \lambda \) bleibt beim Bezugssystemwechsel unverändert.
Zusammen bilden diese Koordinaten an jedem Punkt \( x(\lambda) \) der Kurve
einen vierkomponentigen Vektor
\begin{equation}
u(\lambda) =
\frac {dx(\lambda)}{d\lambda} =
\begin{pmatrix}
c dt(\lambda)/d\lambda \\
d \boldsymbol{x}(\lambda)/d\lambda
\end{pmatrix}
\end{equation}
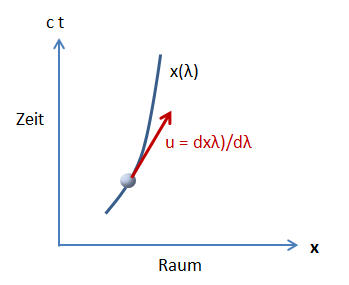
Dieser Vektor liegt an jedem Punkt der Kurve \( x(\lambda) \) tangential an der Kurve an,
ist also ein vierkomponentiger Tangentialvektor (so wie analog der räumliche
Geschwindigkeitsvektor
\( \boldsymbol{v} = d\boldsymbol{x}/dt \)
tangential
an der Bahnkurve \( \boldsymbol{x}(t) \) anliegt und in Bewegungsrichtung zeigt).
Man nennt \( u(\lambda) \) auch die
Vierergeschwindigkeit.
Den Zusammenhang von u mit der Geschwindigkeit v im dreidimensionalen Raum können wir leicht herstellen, denn nach der Kettenregel ist \begin{equation} \frac{d\boldsymbol{x}}{d\lambda} = \frac{d\boldsymbol{x}}{dt} \frac{dt}{d\lambda} = \boldsymbol{v} \frac{dt}{d\lambda} \end{equation} und somit \begin{equation} u = \frac {dx}{d\lambda} = \begin{pmatrix} c dt/d\lambda \\ d \boldsymbol{x}/d\lambda \end{pmatrix} = \frac{dt}{d\lambda} \begin{pmatrix} c \\ \boldsymbol{v} \end{pmatrix} \end{equation} Der vierkomponentige Vektor \( (c, \boldsymbol{v}) \) aus Lichtgeschwindigkeit \(c\) und räumlicher Geschwindigkeit \( \boldsymbol{v} \) muss also nur noch mit der Rate \( dt/d\lambda \) multipliziert werden, mit der die Raumzeitkurve \( x(\lambda) \) bei wachsendem Kurvenparameter \( \lambda \) durch die Zeit \(t\) eilt, und wir erhalten die Vierergeschwindigkeit \(u\).
Nun sind wir gerüstet, einen Impulsvektor zu definieren. Wir werden aber diesmal nicht mit \( \boldsymbol{p} = m \boldsymbol{v} \) versuchen, sondern wir werden den vierkomponentigen Impulsvektor (Viererimpuls) \begin{equation} p = m u = \begin{pmatrix} p^0 \\ \boldsymbol{p} \end{pmatrix} \end{equation} aus konstanter Masse \( m \) und Vierergeschwindigkeit \( u \) bilden. Die drei räumlichen Komponenten 1 bis 3 bilden dabei unseren räumlichen Impulsvektor \( \boldsymbol{p} \) . Für ihn ergibt sich nach den obigen Formeln \begin{equation} \boldsymbol{p} = m \frac{dt}{d\lambda} \boldsymbol{v} \end{equation} d.h. es taucht im Vergleich zur gewohnten Formel von oben noch der Zusatzfaktor \( dt/d\lambda \) darin auf. Ansonsten erfüllt dieser räumliche Impulsvektor aber unsere Erwartungen: Er wächst mit der Trägheit eines (ruhenden) Körpers, die wir in Form der konstanten Ruhemasse \( m \) dargestellt haben, und er wächst mit zunehmender Geschwindigkeit \( \boldsymbol{v} \).
Für die nullte Komponente \( p^0 \) des Viererimpulses ergibt sich \begin{equation} p^0 = m \frac{dt}{d\lambda} c \end{equation} (die hochgestellt Null ist wie immer hier ein Index, also nicht als "hoch Null" zu lesen). Diese Komponente ist also einfach nur die Masse des Objektes, multipliziert mit der Lichtgeschwindigkeit und dem Faktor \( dt/d\lambda \). Was es damit auf sich hat, werden wir noch sehen.
Hier ist nun etwas Vorsicht geboten, damit der Zusatzfaktor \( dt/d\lambda \) nicht zu einer unsinnigen Impulsdefinition führt. Wir müssen die erlaubten Parametrisierungen für unsere Kurve \( x(\lambda) \) durch die Raumzeit so einschränken, dass sie die tatsächliche Bewegung \( \boldsymbol{x}(t) \) widerspiegeln. Wenn wir beispielsweise eine geradlinig-gleichförmige Bewegung betrachten, so wird diese durch eine Gerade in der Raumzeit dargestellt. Dennoch könnten wir im Prinzip den Kurvenparameter \( \lambda \) so wählen, dass diese Gerade an verschiedenen Stellen unterschiedlich schnell mit wachsendem \( \lambda \) durchlaufen wird. Die Kurvenparametrisierung durch \( \lambda \) führt damit eine zusätzliche Freiheit ein, die sich in der tatsächlichen Bewegung nicht widerspiegelt. Diese unphysikalische Freiheit wollen wir wieder einfangen, indem wir verlangen, dass \( dt/d\lambda \) entweder konstant ist oder nur von dem Betrag der tatsächlichen räumlichen Geschwindigkeit \( v = |\boldsymbol{v}| \) abhängt. Bei einer Bewegung mit konstanter Geschwindigkeit wird damit auch unsere Raumzeitkurve \( x(\lambda) \) gleichmäßig mit wachsendem \( \lambda \) durchlaufen. Damit ist gesichert, dass die Vierergeschwindigkeit \( u \) ebenfalls nur von der räumlichen Geschwindigkeit \( \boldsymbol{v} \) abhängt und damit nur diese Geschwindigkeit in einer anderen Form darstellt. Außerdem ist sichergestellt, dass der Impuls nur von Masse und Geschwindigkeit abhängt, so wie wir das aufgrund unserer Erfahrung ja vermuten.
Man fragt sich natürlich: Was bringt uns diese etwas absonderliche Definition einer Vierergeschwindigkeit und eines Viererimpulses? Ganz einfach: Sie erschafft ein Objekt, dessen Veränderung bei einem Bezugssystemwechsel wir sofort angeben können: Da sich die Raumzeitkoordinaten der Bahnkurve nach der einfachen Formel \( x'(\lambda) = \Lambda x(\lambda) \) verändern, verändert sich die Vierergeschwindigkeit \( u \) nach der Formel \begin{equation} u' = \frac {dx'}{d\lambda} = \frac {d (\Lambda x)}{d\lambda} = \Lambda \frac {dx}{d\lambda} = \Lambda u \end{equation} Damit haben wir mit der Vierergeschwindigkeit \( u \) ein Werkzeug in der Hand, mit dem wir die Veränderung der Geschwindigkeit \( \boldsymbol{v} \) eines Objektes bei einem Wechsel des Bezugssystems leicht nachrechnen können. Im Rahmen der Relativitätstheorie würde sich dabei beispielsweise zeigen, dass sich die Eigengeschwindigkeit des Bezugssystem nicht einfach zur Geschwindigkeit des Objekts hinzuaddiert – anders als wir es oben anschaulich angenommen haben (wir führen die konkrete Rechnung weiter unten allerdings nicht explizit durch, um den Rahmen dieses Kapitels nicht zu sprengen).
Da nun \( p = m u \) und \( p' = m u' \) mit konstanter Masse \( m \) ist, gilt analog \( p' = \Lambda p \). Das war der Sinn der ganzen Sache! Vierergeschwindigkeit \( u \) und Viererimpuls \( p \) verändern sich genauso wie die Koordinaten der Bahnkurve! Und damit ist sofort klar: Wenn beispielsweise unser Objekt von oben in zwei Teilobjekte zerfällt und wir für die Viererimpulse vor und nach dem Auseinanderfallen die Impulserhaltung \begin{equation} P = p_1 + p_2 \end{equation} annehmen, so gilt diese Impulserhaltung automatisch auch nach einem Bezugssystemwechsel in ein anderes gleichförmig bewegtes Bezugssystem. Wir können nämlich die obige Gleichung einfach mit der Transformationsmatrix \( \Lambda \) multiplizieren und erhalten \begin{equation} P' = \Lambda P = \Lambda (p_1 + p_2) = \Lambda p_1 + \Lambda p_2 = p'_1 + p'_2 \end{equation} Wenn die Impulserhaltung für Viererimpulse in irgendeinem Inertialsystem gilt, so gilt sie in jedem gleichförmig bewegten Bezugssystem! Das Relativitätsprinzip ist also erfüllt, so wie wir es ebenfalls gefordert haben.
Das Relativitätsprinzip legt damit nahe, dass wir nicht nur die Impulserhaltung für die gewohnten räumlichen Impulse betrachten sollten, sondern dass wir sie auf unsere neuen Viererimpulse ausweiten sollten. Tatsächlich haben wir zu Beginn des Kapitels gesehen, dass die Impulserhaltung die Erhaltung einer weiteren Größe einschließt. Dort war es die Gesamtmasse, die ebenfalls erhalten ist, wenn wir vom Ansatz Impuls gleich Masse mal Geschwindigkeit ausgehen. Ob dies womöglich mit der Null-Komponente des Viererimpulses zusammenhängt? Wir werden sehen ...
Impulserhaltung und Relativitätsprinzip haben uns also dahin geführt, einen Viererimpulsvektor \( p \) zu definieren, der sich aus konstanter Masse \( m \) und Vierergeschwindigkeit \( u \) zusammensetzt. Sind wir damit schon am Ziel? Fast, aber nicht ganz! Wir wissen immer noch nicht, was der ominöse Faktor \( dt/d\lambda \) in den Formeln bedeuten soll, mit dem unsere Bahnkurve \( x(\lambda) \) in der Raumzeit die Zeitkoordinate durchschreitet. Hier kommen wir nur weiter, wenn wir uns Gedanken über die Transformationsmatrix \( \Lambda \) machen, die für die Umrechnung zwischen verschiedenen Bezugssystemen verantwortlich ist. Mit anderen Worten: Wie muss \( \Lambda \) aussehen, um den Wechsel zwischen zwei Bezugssystemen zu beschreiben, die sich beide geradlinig-gleichförmig bewegen, aber mit unterschiedlichen Geschwindigkeiten?
Wie würden wir uns normalerweise den Übergang von einem "ruhenden" Bezugssystem in ein Bezugssystem (ein Raumschiff) vorstellen, das sich mit der Geschwindigkeit \( -\boldsymbol{v} \) bewegt (Vorsicht: Hier ist \( -\boldsymbol{v} \) die Geschwindigkeit des Raumschiff und nicht die Geschwindigkeit des Objektes entlang der Bahnkurve \( x(\lambda) \) )? Was hätten Newton und Galilei dazu gesagt?
Sie hätten ohne zu zögern die folgende Formel
an die Tafel geschrieben:
\begin{equation}
\boldsymbol{x}' = \boldsymbol{x} + \boldsymbol{v} t
\end{equation}
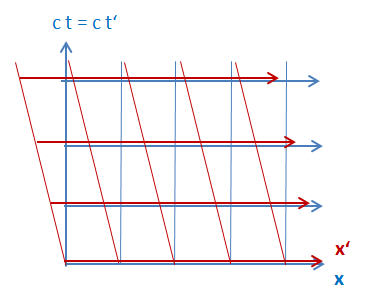
Ein im Nullpunkt ruhendes Objekt mit der Bahnkurve \( \boldsymbol{x}(t) = 0 \) würde sich dann nämlich vom Raumschiff aus gesehen mit der Geschwindigkeit \( \boldsymbol{v} \) bewegen, denn es hätte aus dem Raumschiff betrachtet die Bahnkurve \( \boldsymbol{x}'(t) = \boldsymbol{x}(t) + \boldsymbol{v} t = \boldsymbol{v} t \). Wir kennen das im Grunde schon vom Anfang des Kapitels.
Die Zeit \( t \) ändert sich laut Newton und Galilei bei diesem Bezugssystemwechsel nicht, d.h. eine ruhende Uhr und eine Uhr im Raumschiff laufen ihrer Meinung nach völlig synchron: \begin{equation} t' = t \end{equation} Für alle Physikerinnen und Physiker vor Einstein war das selbstverständlich und kaum einer Erwähnung wert, wie wir aus dem ersten Kapitel über die Zeit wissen. "Die absolute, wahre und mathematische Zeit verfließt an sich und vermöge ihrer Natur gleichförmig und ohne Beziehung auf irgendeinen äußeren Gegenstand" – so hatte es Newton ausgedrückt. Diese Aussage entspricht auch vollkommen unserer eigenen Anschauung darüber, wie sich Zeit verhalten sollte.
Die beiden Umrechnungsformeln \begin{align} t' &= t \\ \boldsymbol{x}' &= \boldsymbol{x} + \boldsymbol{v} t \end{align} können wir auch mithilfe unserer Matrix \( \Lambda \) ausdrücken. Sie sieht dann so aus: \begin{equation} \Lambda = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{v}/c & \boldsymbol{1} \end{pmatrix} \end{equation} wobei \(\boldsymbol{1}\) die 3-mal-3-Einheitsmatrix ist. Die 4-mal-4-Matrix \( \Lambda \) enthält also in ihrer Diagonalen nur Einsen und zusätzlich in ihrer ersten Spalte unter der Eins die drei Geschwindigkeitskomponenten geteilt durch die Lichtgeschwindigkeit. Alle anderen Matrixelemente sind Null. Mit dieser Matrix können wir unsere Transformationsformeln leicht reproduzieren: \begin{equation} x' = \begin{pmatrix} c t' \\ \boldsymbol{x}' \end{pmatrix} = \Lambda x = \begin{pmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{v}/c & \boldsymbol{1} \end{pmatrix} \begin{pmatrix} c t \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} c t \\ \boldsymbol{v} t + \boldsymbol{x} \end{pmatrix} \end{equation} Man nennt eine solche Transformation auch Galilei-Transformation (wobei wir räumliche Drehungen zur Vereinfachung weggelassen haben).
Wie sieht nun der Impuls konkret aus? Dafür müssen wir den Kurvenparameter \( \lambda \) festlegen. Das muss nach unseren Überlegungen von oben so geschehen, dass der Faktor \( dt/d\lambda \) entweder konstant ist oder nur vom Betrag \( v \) der räumlichen Geschwindigkeit abhängt. Außerdem muss die Funktion \( t(\lambda) \), über die unsere Raumzeitkurve \( x(\lambda) \) die Zeitkoordinate \( t \) abfährt, so gestaltet sein, dass sich der Kurvenparameter \( \lambda \) nicht ändert, wenn wir das Bezugssystem wechseln und aus der Zeitkoordinate \( t \) die neue Zeitkoordinate \( t' \) wird.
Die Konstruktion eines passenden Kurvenparameters \( \lambda \) mithilfe der Zeit \( t \) und – falls notwendig – der Geschwindigkeit \( v \) ist hier nun überhaupt kein Problem: Da sich beim Bezugssystemwechsel die Zeit \( t \) nicht ändert (\( t' = t \) ), können wir uns das Leben einfach machen und einfach die Zeitkoordinate \( t \) mit der konstanten Kurvengeschwindigkeit 1 abfahren, also \( t(\lambda) = \lambda \) und damit \( dt/d\lambda = 1 \) wählen. Die obigen Formeln ergeben dann \begin{align} p^0 &= m \frac{dt}{d\lambda} c = m c \\ \boldsymbol{p} &= m \frac{dt}{d\lambda} \boldsymbol{v} = m \boldsymbol{v} \end{align} In der unterenZeile sehen wir den bekannten nichtrelativistische Impuls, wie wir ihn zu Beginn des Kapitels bereits gesehen haben. Außerdem erhalten wir in der oberen Zeile für die Null-Komponente des Viererimpulses die Teilchenmasse, multipliziert mit der Lichtgeschwindigkeit.
Damit unsere Überlegung konsistent ist, muss neben der Impulserhaltung für den Impulsvektor \( \boldsymbol{p} \) auch die Impulserhaltung für die Nullkomponente \( p^0 \) des Viererimpulses \(p\) gelten, denn wir haben die Impulserhaltung ja für den gesamten Viererimpuls \(p\) vorausgesetzt und nicht nur für den üblichen Impuls \( \boldsymbol{p} \). Daraus folgt, dass neben der Impulssumme auch die Massensumme vor und nach einen Ereignis (z.B. einem Zerfall) gleich bleiben muss. Nichtrelativistische Impulserhaltung schließt also automatisch auch die Massenerhaltung mit ein. Masse kann durch Kräfte demnach nicht erschaffen oder zerstört werden.
Wie verändern sich Impuls und Masse eines Objektes, wenn wir von einem "ruhenden" Bezugssystem in das Bezugssystem des Raumschiffs wechseln, dass sich mit der Geschwindigkeit \( -\boldsymbol{v} \) bewegt? Da wir von oben wissen, dass sich der Viererimpuls genauso wie die Raumzeitkoordinaten ändert, nämlich \( p' = \Lambda p \), ist die Antwort sofort klar: \begin{align} m' &= m \\ \boldsymbol{p}' &= \boldsymbol{p} + m \boldsymbol{v} \end{align} Zum alten Impuls kommt aufgrund der Geschwindigkeitsänderung also noch der Zusatzimpuls \( m \boldsymbol{v} \) hinzu, während die Masse \( m \) sich überhaupt nicht ändert – die Trägheit ist konstant.
Das entspricht alles unserer Anschauung, und dennoch erweist es sich letztlich als falsch, denn unsere Überlegungen zum Relativitätsprinzip stimmen nur dann näherungsweise, wenn die Geschwindigkeiten klein gegenüber der Lichtgeschwindigkeit sind. Schauen wir uns also nun an, wie die Natur in Wirklichkeit funktioniert – auch wenn die Geschwindigkeiten groß werden.
Wenn wir Einsteins Relativitätstheorie berücksichtigen, können die obigen Formeln nicht korrekt sein, denn die Geschwindigkeit \( \boldsymbol{v} \) unterliegt darin keinen Beschränkungen. Unser Raumschiff kann bisher beliebig schnell sein. Nach Einsteins spezieller Relativitätstheorie kann aber nichts schneller als das Licht sein. Außerdem fliegt ein Lichtblitz immer gleich schnell, auch wenn wir zwischendurch das Bezugssystem wechseln und ihm mit einem Raumschiff hinterherfliegen.
Wie also sehen die richtigen Transformationsformeln für einen Wechsel vom "ruhenden" Bezugssystem in das Bezugssystem des Raumschiffs aus, dass sich mit der Geschwindigkeit \( -\boldsymbol{v} \) bewegt. Wie lautet unsere entsprechende Matrix \( \Lambda \)?
Wir wollen uns die entsprechende Herleitung hier ersparen – man findet sie beispielsweise in Wikipedia: Lorentz-Transformation. Statt dessen wollen wir einfach nur überprüfen, dass die gleichsam vom Himmel gefallene Matrix \( \Lambda \) genau das tut, was wir von ihr erwarten. Hier also ist sie – man nennt sie die Matrix der Lorentz-Transformation: \begin{equation} \Lambda = \begin{pmatrix} \gamma & \gamma \boldsymbol{v}/c \\ \gamma \boldsymbol{v}/c & \gamma \boldsymbol{1} \end{pmatrix} \end{equation} Für Zeit- und Ortskoordinaten ausgeschrieben ergibt das: \begin{align} c t' &= \gamma \, (c t + \boldsymbol{v x}/c) \\ \boldsymbol{x}' &= \gamma \, (\boldsymbol{x} + \boldsymbol{v} t) \end{align} Die untere Formel entspricht bis auf den Faktor \( \gamma \) genau unserer nichtrelativistischen Formel \( \boldsymbol{x}' = \boldsymbol{x} + \boldsymbol{v} t \) von etwas weiter oben, wie sie Newton und Galilei hingeschrieben hätten. Wir erwarten also, dass bei kleinen Geschwindigkeiten der neu hinzugekommene Faktor \( \gamma \) nahezu Eins werden muss – kein Zufall, denn natürlich wird sich \( \gamma \) als der uns bereits bekannte Lorentzfaktor erweisen, was wir aber hier noch herausarbeiten wollen. In der Formel ist \( \gamma \) dann für die Lorentzkontraktion von Längen zuständig, die uns im Kapitel über den Raum begegnet ist.
Die Umwandlungsformel für die Zeit ist wesentlich komplizierter als
die einfache Formel \( t' = t \) von weiter oben.
Hier sorgt der Vorfaktor \( \gamma \) für die Zeitdilatation,
die bewegte Uhren langsamer laufen lässt.
Etwas überaschend erscheint noch ein Zusatzterm
\( \boldsymbol{v x}/c \), der
zu einer Verschiebung von Ereignissen in der Zeit führt.
Hier spiegelt sich wider, dass verschiedene Beobachter die Gleichzeitigkeit von
Ereignissen unterschiedlich beurteilen – siehe unser Kapitel über die Zeit.
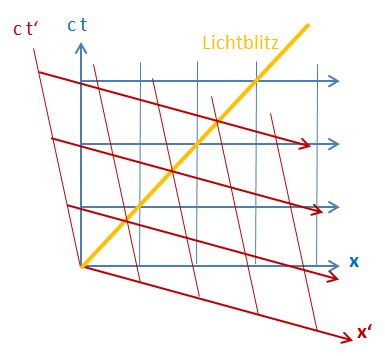
In den Formeln stecken also jede Menge physikalische Phänomene, über die man ganze Bücher schreiben könnte. Wir wollen hier nicht so weit gehen, sondern nur zwei Spezialfälle untersuchen: Was geschieht, wenn wir ein ruhendes Objekt aus unserem bewegten Raumschiff heraus betrachten, und was geschieht, wenn wir dasselbe mit einem Lichtblitz tun?
Ein im Koordinatenursprung ruhendes Objekt können wir durch die Bahnkurve \( \boldsymbol{x}(t) = 0 \) beschreiben. Setzen wir dies in den obigen Formeln ein, so erhalten wir \begin{align} c t' &= \gamma c t \\ \boldsymbol{x}'(t) &= \gamma \boldsymbol{v} t \end{align} Die obere Formel können wir nun dazu verwenden, um in der unteren Formel rechts das Produkt \( \gamma t \) durch \( t' \) zu ersetzen: \begin{equation} \boldsymbol{x}'(t') = \boldsymbol{v} t' \end{equation}
Genau so muss es sein! Das ruhende Objekt bewegt sich vom Raumschiff aus gesehen mit der Geschwindigkeit v, wobei wir den Zeitmaßstab berücksichtigen müssen, den eine mitgeführte Uhr im Raumschiff liefert.
Nun zu unserem Lichtblitz, der sich natürlich mit Lichtgeschwindigkeit \(c\) bewegt. Seine Flugrichtung kennzeichnen wir durch den Einheitsvektor \( \boldsymbol{e} \), der die Länge 1 haben soll. Die Bahnkurve des Lichtblitzes ist also gegeben durch die Formel \( \boldsymbol{x}(t) = c t \, \boldsymbol{e} \). Unser Raumschiff soll sich wieder mit der Geschwindigkeit \( -\boldsymbol{v} \) genau in der Gegenrichtung bewegen, d.h. \( \boldsymbol{v} = v \, \boldsymbol{e} \). Setzen wir die Bahnkurve des Lichtblitzes \( \boldsymbol{x}(t) = c t \, \boldsymbol{e} \) oben in die Transformationsformeln ein, so wird aus dem Raumschiff heraus gesehen diese Bewegung des Lichtblitzes durch folgende Koordinaten beschrieben: \begin{align} c t' &= \gamma \, (c t + c t \, \boldsymbol{v \boldsymbol{e}}/c) = \gamma \, (c + v) \, t \\ \boldsymbol{x}'(t) &= \gamma \, (c t \, \boldsymbol{e} + v \, \boldsymbol{e} t) = \gamma \, (c + v) \, \boldsymbol{e} \, t \end{align} und somit \begin{equation} \boldsymbol{x}'(t') = c \, t' \boldsymbol{e} \end{equation} Auch vom Raumschiff aus gesehen bewegt sich der Lichtblitz also mit Lichtgeschwindigkeit. Man sieht hier, wie wichtig der merkwürdige zweite Summand in der Formel für \( c t' \) ist, denn ohne ihn würde die Rechnung nicht aufgehen.
Bisher ist also alles in schönster Ordnung mit unseren Transformationsformeln in die Koordinaten des Raumschiffs. Sie tun genau das, was wir erwarten. Allerdings haben wir bisher noch keinerlei Aussage über den Vorfaktor \( \gamma \) erhalten, der sich ja als der bekannte Lorentzfaktor herausstellen soll. Die obigen Rechnungen hätten mit jedem beliebigen Wert für \( \gamma \) funktioniert, sogar mit dem trivialen Wert Eins. Was also legt \( \gamma \) fest?
Man muss einen weiteren Gedanken hinzunehmen, um \( \gamma \) festzulegen. Mathematisch würde man sagen: Man muss die Gruppenstruktur berücksichtigen, die unsere Transformation haben soll, insbesondere die Tatsache, dass eine entgegengesetzte Geschwindigkeit beim Bezugssystemwechsel zur inversen Transformationsmatrix führen muss. Physikalisch bedeutet das: Wenn ich von einem Bezugssystem mit Raumzeit-Koordinaten \( x \) zu einem mit \( -\boldsymbol{v} \) relativ dazu bewegten Bezugssystem mit Koordinaten \( x' = \Lambda_{-\boldsymbol{v}} \, x \) übergehe und anschließend zu einem weiteren Bezugssystem mit Koordinaten \( x'' = \Lambda_{\boldsymbol{v}} \, x' \) wechsle, das sich relativ zu \( x' \) mit der umgekehrten Geschwindigkeit \( \boldsymbol{v} \) bewegt, so sollte ich mich wieder im ursprünglichen Bezugssystem befinden, sodass \( x'' = x \) gilt. Es muss also für das Matrixprodukt \begin{equation} \Lambda_{\boldsymbol{v}} \, \Lambda_{-\boldsymbol{v}} = 1 \end{equation} gelten, wobei 1 für die Einheitsmatrix steht. Rechnen wir das Matrixprodukt aus: \begin{align} \Lambda_{\boldsymbol{v}} \, \Lambda_{-\boldsymbol{v}} &= \begin{pmatrix} \gamma & \gamma \boldsymbol{v}/c \\ \gamma \boldsymbol{v}/c & \gamma \boldsymbol{1} \end{pmatrix} \begin{pmatrix} \gamma & -\gamma \boldsymbol{v}/c \\ -\gamma \boldsymbol{v}/c & \gamma \boldsymbol{1} \end{pmatrix} = \\ & \\ &= \gamma^2 \, \begin{pmatrix} 1 & \boldsymbol{v}/c \\ \boldsymbol{v}/c & \boldsymbol{1} \end{pmatrix} \begin{pmatrix} 1 & -\boldsymbol{v}/c \\ -\boldsymbol{v}/c & \boldsymbol{1} \end{pmatrix} = \\ & \\ &= \gamma^2 \, \begin{pmatrix} (1 - (v/c)^2) & -\boldsymbol{v}/c + \boldsymbol{v}/c \\ \boldsymbol{v}/c - \boldsymbol{v}/c & (-(v/c)^2 + 1) \, \boldsymbol{1} \end{pmatrix} = \\ & \\ &= \gamma^2 \, \begin{pmatrix} (1 - (v/c)^2) & \boldsymbol{0} \\ \boldsymbol{0} & (1 - (v/c)^2) \, \boldsymbol{1} \end{pmatrix} = \\ & \\ &= \gamma^2 \, (1 - (v/c)^2) \, 1 \end{align} Das Matrixprodukt ergibt also vor der Einheitsmatrix 1 den Vorfaktor \( \gamma^2 (1 - (v/c)^2) \). Es soll aber nur die Einheitsmatrix herauskommen. Also muss der Vorfaktor gleich der Zahl Eins sein: \begin{equation} \gamma^2 \, (1 - (v/c)^2) = 1 \end{equation} Umgestellt ergibt das unsere gesuchte Formel für \( \gamma \), nämlich \begin{equation} \gamma = \sqrt { \frac {1} {1 - (v/c)^2} } \end{equation} (wir wählen das Vorzeichen von \( \gamma \) per Konvention positiv, da wir uns momentan nicht für Raumzeit-Spiegelungen interessieren). Das ist genau der Lorentzfaktor, den wir bereits in den vorhergehenden Kapiteln kennengelernt haben!
Damit haben wir uns mit der etwas ungewohnten Art, wie sich Raum und Zeit bei einem Bezugssystemwechsel in Wirklichkeit verhalten, einigermaßen vertraut gemacht. Nun sind wir gerüstet, uns der Vierergeschwindigkeit und schließlich dem Impuls zuzuwenden.
Dafür müssen wir wieder den Kurvenparameter \( \lambda \) für unsere Raumzeitkurve \( x(\lambda) \) als Funktion der Zeit \( t \) und ggf. der Geschwindigkeit \( v \) festlegen, sodass der Faktor \( dt/d\lambda \) entweder konstant ist oder vom Betrag \( v \) der räumlichen Geschwindigkeit abhängt und außerdem \( \lambda \) sich bei einem Wechsel des Bezugssystems nicht ändert. Die einfache Wahl \( \lambda = t \) wie im nichtrelativistischen Fall scheidet hier aus, denn \( t \) verändert sich beim Bezugssystemwechel.
Wir kennen jedoch aus dem Kapitel über die Zeit bereits einen Parameter, der eng mit der Zeit verwandt ist und der nicht von irgendeinem Bezugssystem abhängt: Es ist die Eigenzeit \( \tau \), wie sie auf einer mitgeführten Uhr angezeigt wird, die sich entlang unserer Bahnkurve \( x(\lambda) \) durch Raum und Zeit bewegt. Erinnern wir uns, was wir im ersten Kapitel über die Eigenzeit \( \tau \) erfahren haben: Legt ein Körper auf der Bahnkurve \( x(\lambda) \) während des sehr kurzen (infinitesimalen) Zeitintervalls \( dt \) die ebenfalls sehr kurze Wegstrecke \( ds = v \, dt \) zurück, so vergeht für ihn die Eigenzeit \( d\tau \). Dabei gilt für deren Quadrat: \begin{align} d\tau^2 &= dt^2 - (ds/c)^2 = \\ &= dt^2 - (v \, dt/c)^2 = \\ &= dt^2 \, (1 - (v/c)^2) = \\ &= (dt/\gamma)^2 \end{align} also \( d\tau = dt/\gamma \) mit dem Lorentzfaktor \( \gamma \) (in den obigen Formeln ist jetzt \(v\) die Geschwindigkeit der Uhr entlang der Bahnkurve und nicht die Geschwindigkeit des Raumschiffs beim Wechsel des Bezugssystems – bitte nicht verwechseln!). Bei einem Wechsel des Bezugssystems verändert sich nun zwar nach den obigen Formeln das Zeitintervall \(dt\) zu \(dt'\) (Zeitdilatation) und die kurze Wegstrecke \( ds = |\boldsymbol{dx}| \) zu \( ds' = |\boldsymbol{dx'}| \) (Lorentzkontraktion), aber wir können leicht nachrechnen, dass \begin{equation} (c \, dt)^2 - (ds)^2 = (c \, dt')^2 - (ds')^2 \end{equation} gilt und dass sich entsprechend auch \( d\tau \) nicht ändert. Wenn wir nun die kleinen Eigenzeitintervalle \( d\tau \) entlang der Raumzeit-Bahnkurve aufintegrieren, so erhalten wir damit unseren gewünschten Bahnparameter \begin{equation} \lambda = \tau \quad \mathrm{sodass} \quad \frac{dt}{d\lambda} = \frac{dt}{d\tau} = \gamma \end{equation} Unser Vorfaktor \( dt/d\lambda \) hängt also wie gewünscht nur vom Betrag der räumlichen Geschwindigkeit ab, denn dies gilt auch für den Lorentzfaktor \( \gamma \).
Damit haben wir nun alle Zutaten für den Impuls zusammen: Er sieht fast genauso aus wie der nichtrelativistische Impuls von oben, nur dass wegen \( dt/d\lambda \) als Zusatzfaktor der Lorentzfaktor \( \gamma \) hinzukommt: \begin{align} p^0 &= m \frac{dt}{d\lambda} c = m \gamma c \\ \boldsymbol{p} &= m \frac{dt}{d\lambda} \boldsymbol{v} = m \gamma \boldsymbol{v} \end{align} Wenn die Impulserhaltung für Impuls-Vierervektoren \( p = (p^0, \boldsymbol{p}) \) in einem Bezugssystem gilt, so gilt sie auch in jedem anderen Bezugssystem, das sich relativ dazu geradlinig-gleichförmig bewegt – das haben wir uns oben überlegt. Das ist nicht trivial, denn \( p \) und damit \( p^0 \) und \( \boldsymbol{p} \) verändern sich sehr wohl, wenn wir das Bezugssystem wechseln. Sie tun dies aber gerade so, dass die Erhaltung für alle beteiligten Impulse \( \boldsymbol{p} \) und zusätzlich für alle beteiligten Null-Komponenten \( p^0 \) dadurch nicht zerstört wird, wie wir weiter oben nachgewiesen haben.
Im nichtrelativistischen Fall hatte die Erhaltung der Null-Komponente \( p^0 \) dazu geführt, dass sich die Summe aller beteiligten Massen bei einem Prozess nicht ändernt. Masse konnte dort weder erzeugt noch vernichtet werden. Außerdem veränderte sich die Masse bei einem Wechsel des Bezugssystems nicht.
Das ist nun anders! Die Masse \( m \) eines Teilchens ändert sich zwar nach wie vor nicht, wenn wir das Bezugssystem wechseln, denn genau so hatten wir die Masse oben festgelegt: als unveränderliche Eigenschaft eines Teilchens. Was sich aber sehr wohl ändert, ist die Trägheit eines Teilchens, denn diese ist durch das Produkt \( m \gamma \) gegeben – wir hatten das im letzten Kapitel bereits diskutiert. Die Trägheit wird umso größer, je schneller sich das Teilchen bewegt! So lässt sich ein sehr schnelles Teilchen kaum noch weiter beschleunigen, denn seine Trägheit wird unendlich groß, wenn sich seine Geschwindigkeit \(v\) der Lichtgeschwindigkeit \(c\) nähert. Daher kann die Lichtgeschwindigkeit für ein massives Teilchen nie erreicht oder gar überschritten werden.
Außerdem bleibt nicht die Massensumme, sondern die Summe aller \( p^0 \)-Komponenten und damit die Summe aller Teilchen-Trägheiten \( m \gamma \) bei einem Prozess erhalten! So kann ein massives ruhendes Teilchen mit Masse \( M \) beispielsweise in zwei sehr viel leichtere Teilchen mit identischen Massen \( m \) zerfallen, wobei dann \begin{equation} M = 2 m \gamma \end{equation} gelten muss. Wenn die Masse \( m \) der entstandenen Teilchen sehr viel kleiner ist als die Masse \( M \) des zerfallenen Teilchens, so muss der Lorentzfaktor \( \gamma \) entsprechend groß sein, damit die obige Bilanz aufgeht. Das bedeutet, dass die beiden Teilchen mit entsprechend hoher Geschwindigkeit auseinanderfliegen müssen. Diese Geschwindigkeit ist vollständig durch die Differenz der Teilchenmassen vor und nach dem Zerfall festgelegt. Man kann das so interpretieren, dass ihre Bewegungsenergie aus der Masse des zerfallenen Teilchens stammt! Es wird sich daher im nächsten Kapitel als sinnvoll erweisen, die Null-Komponente \( p^0 \) (per Konvention multipliziert mit der Lichtgeschwindigkeit \(c\) ) als Energie \(E\) des Teilchens zu interpretieren: \begin{equation} E = p^0 c = m \gamma c^2 \end{equation} Energie, Masse und Trägheit eines Teilchens hängen damit eng miteinander zusammen. Die Erhaltung der Summe aller Null-Komponenten der Viererimpulse entspricht damit der Erhaltung der Gesamtenergie. Sie ersetzt die Erhaltung der Gesamtmasse aus der nichtrelativistischen Physik. Mehr dazu im nächsten Kapitel!
Wie klein kann die Masse \( m \) der Teilchen werden, die bei dem obigen Teilchenzerfall entstehen? Tatsächlich können wir in der Gleichung \( M = 2 m \gamma \) die Masse \( m \) beliebig klein werden lassen, solange wir dies durch einen entsprechend großen Lorentzfaktor \( \gamma \) wieder ausgleichen. Wir können uns sogar vorstellen, dass wir die Masse \( m \) gegen Null gehen lassen, wobei die Geschwindigkeit \(v\) der beiden Teilchen jeweils gegen die Lichtgeschwindigkeit \(c\) geht, sodass \( m \gamma = p^0/c \) konstant bleibt. Der Viererimpuls geht dann gegen \( p = (p^0, p^0 \boldsymbol{e}) \) mit konstantem \( p^0 \), wobei \( \boldsymbol{e} = \boldsymbol{c}/c \) der Einheitsvektor in Bewegungsrichtung ist.
Können wir die Masse \( m \) tatsächlich sogar gleich Null setzen? Gibt es masselose Teilchen?
Ohne die spezielle Relativitätstheorie wäre die Antwort ein klares NEIN, denn der Impuls eines solchen Teilchens wäre immer Null. Unsere obige Überlegung hat aber gezeigt, dass es in der speziellen Relativitätstheorie durchaus solche Teilchen geben könnte, denn wir können wie gerade gesehen in der Definition \( p = m u \) des Viererimpulses den Grenzübergang \( m \) gegen Null durchführen, indem wir fordern, dass dabei \( p^0 = m \gamma c \) konstant bleibt so wie in unserem Zerfallsbeispiel. Der Viererimpuls eines masselosen Teilchens ist dann \( p = (p^0, p^0 \boldsymbol{e}) \). Anders als im nichtrelativistischen Fall bleibt die Geschwindigkeit bei diesem Grenzübergang endlich – sie wird gleich der Lichtgeschwindigkeit.
Und tatsächlich macht die Natur Gebrauch von dieser Möglichkeit, denn das Photon ist ein solches masselose Teilchen! Ein massives ruhendes Teilchen könnte also durchaus in zwei masselose Photonen zerfallen, und das neutrale Pion tut genau dies! Die Masse des Pions geht dabei vollständig verloren und findet sich in den \(p^0\)-Komponenten der beiden Photonen wieder, also in der Energie der Photonen.
Dass masselose Teilchen möglich sind, zeigt auch die folgende Überlegung: Ganz allgemein gilt für jeden Vierervektor, der beim Bezugssystemwechsel mit der Matrix \( \Lambda \) multipliziert wird, dass die Differenz aus quadrierter Null-Komponente minus quadrierter räumlicher Vektorkomponente sich dabei nicht ändert, auch wenn sich die Terme einzeln sehr wohl ändern. Genau so hatten wir ja beispielsweise die Eigenzeit \( \&tau \) konstruiert. Diese Eigenschaft ist charakteristisch für die Lorentzmatrix \( Lambda \). Sie gilt auch für unsere Vierergeschwindigkeit \(u\) und den daraus abgeleiteten Viererimpuls \(p\), da beide ebenfalls beim Bezugssystemwechsel mit der Matrix \( Lambda \) multipliziert werden. Also muss \( (p^0)^2 - \boldsymbol{p}^2 \) in jedem Bezugssystem denselben Wert haben (die hochgestellte 0 ist dabei ein Index, während die hochgestellte 2 das Quadrieren bezeichnet). Setzen wir hier unsere Formeln \( p^0 = m \gamma c \) und \( \boldsymbol{p} = m \gamma \boldsymbol{v} \) ein, so finden wir als Ergebnis \begin{align} (p^0)^2 - \boldsymbol{p}^2 &= (m \gamma c)^2 - (m \gamma v)^2 = \\ &= m^2 \gamma^2 (c^2 - v^2) = \\ &= m^2 \frac{1}{1 - (v/c)^2} (c^2 - v^2) = \\ &= (mc)^2 \end{align} Das passt, denn die Teilchenmasse \(m\) ist unabhängig vom Bezugssystem. Außerdem sehen wir, dass wir in dieser Formel die Teilchenmasse \(m\) problemlos gleich Null setzen können, d.h. die Formel gilt auch für masselose Teilchen wie Photonen. Es ist schon erstaunlich, was man alles ableiten kann, wenn man die Impulserhaltung, das Relativitätsprinzip und die Konstanz der Lichtgeschwindigkeit voraussetzt und einen dazu passenden Ansatz für den Impulsbegriff, bestehend aus Trägheit und Geschwindigkeit, hineinsteckt!
Im letzten Kapitel hatten wir bereits angesprochen, dass Newtons Wechselwirkungsprinzip Actio gleich Reactio dem Impulserhaltungssatz entspricht. Innere Kräfte können den Gesamtimpuls nicht ändern. Allerdings stimmt das Wechselwirkungsprinzip nur dann, wenn die Zeit, die eine Kraftübertragung zwischen zwei Körpern benötigt, vernachlässigt werden kann.
Im allgemeinen Fall muss man die Zeit für eine Kraftübertragung zwischen zwei Körpern jedoch berücksichtigen. Der Gesamtimpuls zweier Körper ist dann scheinbar für eine gewisse Zeit nicht erhalten. Wenn wir jedoch davon ausgehen, dass die Impulserhaltung ein ganz allgemeines Naturgesetz ist, so müssen wir uns fragen: Wo steckt der fehlende Impuls in der Zwischenzeit?
Schaut man sich die Gleichungen für ein elektromagnetisches Feld – die Maxwellgleichungen – genauer an,
so stellt man fest, dass sich der fehlende Impuls im elektromagnetischen Feld versteckt.
Auch elektromagnetische Felder haben demnach einen Impuls oder genauer: eine Impulsdichte (Impuls
pro Raumvolumen)!
Wenn wir an die oben angesprochenen Photonen denken, so überrascht uns das nicht:
Photonen entsprechen ja den Quantenteilchen des Lichts, und da Photonen einen Impuls besitzen,
so muss auch der zugehörige Lichtstrahl einen Impuls tragen.
Die Impulsdichte \( \boldsymbol{S} \) (auch Pointing-Vektor genannt)
lässt sich nun durch das elektrische
Feld \( \boldsymbol{E} \) und das Magnetfeld \( \boldsymbol{B} \) ausdrücken:
\begin{equation}
\boldsymbol{S} \sim \boldsymbol{E} \times \boldsymbol{B}
\end{equation}
wobei \( \times \) für das Vektor-Kreuzprodukt steht
(Achtung: \( \boldsymbol{E} \) ist hier das elektrische Feld und nicht die Energie,
die wir auch mit dem Buchstaben \(E\) bezeichnet hatten).
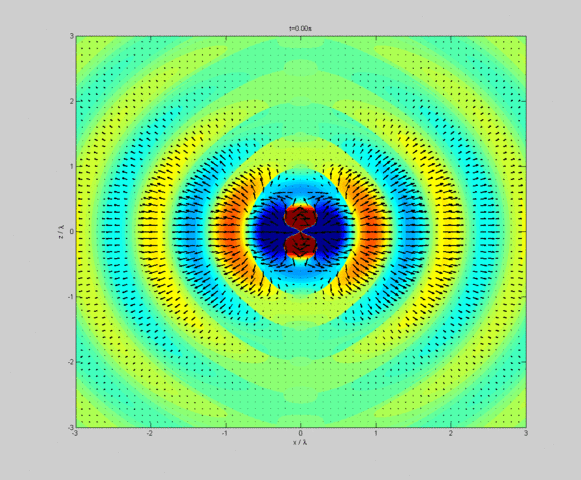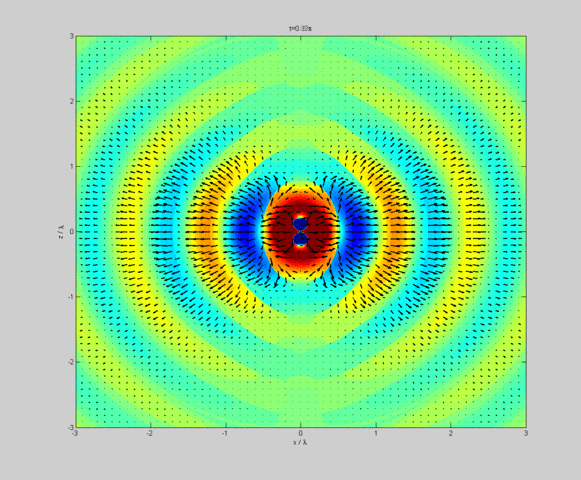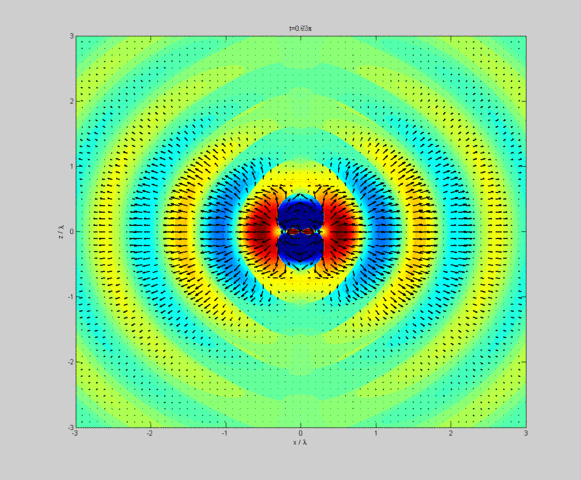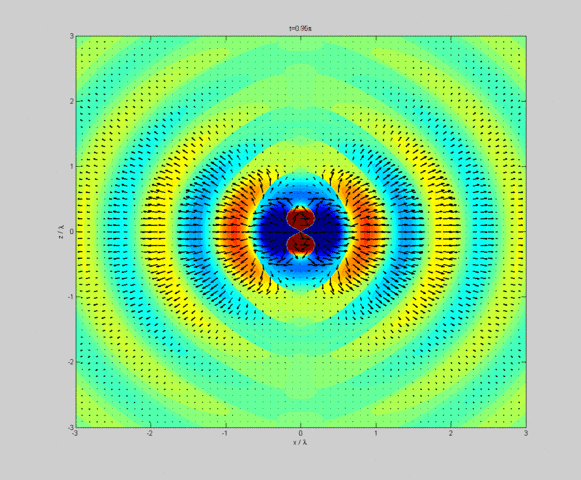
Quelle:
Wikimedia Commons File:DipoleRadiation.gif von Geoemyda.
Lizenz: Creative Commons Attribution-Share Alike
3.0 Unported,
2.5 Generic, 2.0 Generic and 1.0 Generic license.
Damit nicht genug: Ein elektromagnetisches Feld besitzt sogar eine Trägheit, ähnlich wie ein massives Teilchen. Wieder überrascht das nicht, denn auch zwei Photonen, die man in einer masselosen Kiste einsperrt, sodass sie ständig darin entgegengesetzt zueinander hin- und herpendeln, verleihen der Kiste dadurch eine Trägheit wie eine Masse – der Gesamt-Viererimpuls \(P\) der beiden Photonen in der ruhenden Kiste beträgt nämlich \begin{equation} P = \begin{pmatrix} p^0 \\ p^0 \boldsymbol{e} \end{pmatrix} + \begin{pmatrix} p^0 \\ -p^0 \boldsymbol{e} \end{pmatrix} = \begin{pmatrix} 2p^0 \\ \boldsymbol{0} \end{pmatrix} \end{equation} und verhält sich damit genau wie der Viererimpuls eines ruhenden Teilchens mit Masse \( M = 2 p^0/c \) . Anders ausgedrückt: Die eingeschlossene Gesamtenergie \( E = 2 p^0 c = M c^2 \) der beiden Photonen verleiht dem Kasten dieselbe Trägheit wie ein ruhendes Teilchen mit Masse \(M\). Masse ist von eingeschlossener, also lokalisierter Energie nicht zu unterscheiden, und es spricht vieles dafür, dass letztlich jede Teilchenmasse nichts anderes als eingeschlossene Energie ist. So hat ein großer Teil der Masse eines Protons und eines Neutrons seine Ursache nicht in den Massen der drei Quarks, aus denen sie bestehen, sondern sie stammt aus der Feldenergie des starken Gluonenfeldes, das die Quarks zusammenhält.
Kann man anschaulich verstehen, wieso ein elektromagnetisches Feld eine Trägheit aufweisen kann? Letztlich liegt es an der endlichen Ausbreitungsgeschwindigkeit von elektrischen Kräften. Schauen wir uns als Beispiel eine gleichmäßig elektrisch geladene Kugel im leeren Weltraum an. Solange die Kugel ruht oder sich gleichmäßig bewegt, sind die elektrischen Kräfte mit den Kräften, die die Kugelform aufrecht erhalten, im Gleichgewicht, und die Gesamtkraft auf die Kugel ist nach Newtons Wechselwirkungsprinzip (Actio gleich reactio) Null. Wird die Kugel jedoch beschleunigt, so macht sich die endliche Ausbreitungsgeschwindigkeit von Kräften bemerkbar. Die Einflüsse der verschiedenen geladenen Teile der Kugel aufeinander verändern sich, und das Kraftgleichgewicht wird gestört. Man kann nachrechnen, dass eine resultierende Gesamtkraft übrig bleibt, die der Beschleunigung entgegen wirkt und sich wie die Trägheit einer Masse \(m\) auswirkt, die sich nach der Formel \( E = m c^2 \) aus der Gesamtenergie \(E\) des elektromagnetischen Feldes und der Felder der inneren Kugelkräfte zusammensetzt.
Felder besitzen also Energie und Impuls, wobei sich die Energie als Trägheit äußert. Wie bei einem Teilchen hängen auch Energie und Impuls bei einem Feld eng miteinander zusammen. Da ein Feld aber nicht punktförmig wie ein idealisiertes Teilchen ist, bilden beide zusammen nicht einfach einen Vierer-Impulsvektor. Statt dessen treten Energie- und Impulsdichten auf, die von Raum und Zeit abhängen. Wie hängen diese nun miteinander zusammen?
Man kann das rerlativ leicht erraten, indem man statt eines einzelnen Teilchens eine große Ansammlung von Teilchen mit gleicher Masse \(m\), gleicher Energie \(E\) und gleichem Impuls \( \boldsymbol{p} \) betrachtet, die sich mit einer konstanten Teilchendichte \(n\) im Raum verteilen (\(n\) gibt dabei die Teilchenanzahl pro Volumen an). Energiedichte \( \omega \) und Impulsdichte \( \boldsymbol{S} \) dieser Teilchen ist dann gleich \begin{align} \omega &= n \, E = n \, m \gamma c^2 \\ \boldsymbol{S} &= n \, \boldsymbol{p} = n \, m \gamma \boldsymbol{v} \end{align} und somit \begin{equation} \boldsymbol{S} = \frac{\omega}{c^2} \, \boldsymbol{v} \end{equation} Hier spielt die Masse \(m\) wieder keine Rolle, d.h. dieser Zusammenhang zwischen Energiedichte \(\omega\) und Impulsdichte \(\boldsymbol{S}\) gilt auch für masselose Teilchen. Man kann die obige Überlegung auch auf andere Teilchenansammlungen verallgemeinern, und sie gilt auch für Felder. Ganz allgemein gilt:
Dabei zählen wir für einen massiven Teilchenschwarm die Masse mit zur Energie hinzu, d.h. die gesamte Trägheit \( m \gamma \) bestimmt nach Multiplikation mit \( c^2 \) die Energie der Teilchen. Das macht Sinn, denn umgekehrt bedeutet ja auch eine lokalisierte Feldenergie eine Trägheit. Man könnte daher auch sagen: Immer wenn sich etwas mit Trägheit bewegt, entsteht ein Impuls. Das entspricht sogar ganz anschaulich unserem intuitiven Impulsverständnis – das Überaschende dabei ist höchstens, dass wir nicht damit gerechnet hätten, dass auch eine Feldenergie eine Trägheit besitzt.
Bei einer Materieverteilung, die Felder und Teilchenverteilungen umfassen kann, haben wir es also mit Energie- und Impulsdichten zu tun. War es das schon?
Nicht ganz, denn anders als bei nur einem einzigen Teilchen kann es bei einer Materieverteilung zum Austausch von Energie und Impuls zwischen den einzelnen Raumbereichen kommen. Es können Energieströme auftreten, wobei wir gerade gesehen haben, dass ein Energiestrom zu einer Impulsdichte führt. Wenn wir Einflüsse von außen ausschließen, so kann dabei Energie weder erzeugt werden noch verloren gehen. Man drückt dies mathematisch durch eine Kontinuitätsgleichung aus, die inhaltlich besagt: Wenn die Energie in einem Raumbereich sich ändert, so muss es einen dazu passenden Energiestrom durch den Rand dieses Raumbereichs geben. Energiedichte und Energiestrom (und zugehörige Impulsdichte) hängen also eng miteinander zusammen.
Dasselbe gilt auch für die Impulsdichte: Wenn der Impuls in einem Raumbereich sich ändert, so muss es einen dazu passenden Impulsstrom durch den Rand dieses Raumbereichs geben. Einen solchen Impulsstrom können wir auch als Kraft-Flächendichte (Spannung) interpretieren, denn er führt ja zu einer Änderung des Impulses der Materie im betrachteten Raumbereich, und Impulsänderungen entstehen nach Newtons Aktionsprinzip durch Kräfte.
Es entsteht also ein Geflecht aus mehreren Größen, die alle miteinander zusammenhängen: Energiedichten, Energiedichteflüssen = Impulsdichten und Impulsdichteflüssen = Kraftdichten. Außerdem werden sich diese Größen bei einem Wechsel von einem ruhenden in ein gleichförmig bewegtes Bezugsystem ändern. Mathematisch kann man all dies recht elegant im Rahmen des sogenannten Energie-Impuls-Tensors zusammenführen – er ist bei einer allgemeinen Materie-Feld-Verteilung das Gegenstück zum Viererimpuls eines einzelnen Teilchens. Während jedoch der Viererimpuls nur 4 Komponenten besitzt, weist der Energie-Impuls-Tensor 4-mal-4 = 16 Komponenten auf, von denen wegen Symmetrie aber nur 7 unabhängig sind. Die 0-0-Komponente ist dabei die Energiedichte, die 0-k-Komponenten = k-0-Komponenten (mit k = 1, 2, 3) sind die Energiedichteflüsse = Impulsdichten und die k-k-Komponenten sind die Impulsdichteflüsse = Kraftdichten.
In Einsteins Allgemeiner Relativitätstheorie der Gravitation ist nun dieser gesamte Energie-Impuls-Tensor die Quelle des Gravitationsfeldes. Das bedeutet beispielsweise: Nicht nur Massen- und Energiedichten, sondern auch Drücke (isotrope Kraftdichten) sind Quellen des Gravitationsfeldes – wobei, wie wir wissen, negative Drücke (innere Zugkräfte) gravitativ abstoßend wirken. Das ist der Grund dafür, warum bestimmte Materieformen wie beispielsweise ein Inflatonfeld oder die geheimnisvolle Dunkle Energie, die beide einen starken negativen Druck besitzen, zu einer beschleunigten Expansion des Universums führen können. Bei einem Neutronenstern, der sich mit stark positivem (also normalem) Druck gegen den gravitativen Kollaps wehrt, ist es dagegen umgekehrt: Der starke Druck bewirkt eine zusätzliche anziehende Gravitation, die den Neutronenstern bedrängt. Bei zuviel Sternenmasse reicht daher auch ein noch so starker Druck nicht mehr aus, den Kollaps abzuwenden, und ein schwarzes Loch entsteht.
Es ist wie so oft in der Physik: Erst wenn man alles konsistent zusammenfügt, so ergibt sich das korrekte Bild von der Natur, und dieses stimmt nicht immer mit dem Bild überein, das wir intuitiv erwarten würden.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 11 February 2023