
Quelle: Wikimedia Commons File:Ernst Mach 01.jpg, dort public domain; aus Zeitschrift für Physikalische Chemie, Band 40, von 1902
Der intuitive Realitätsbegriff
Realität in der klassischen Welt
Realität in der Quantenwelt
Im letzten Kapitel der Reihe Grundfragen der Physik
wollen wir uns einem Thema zuwenden, das eng mit vielen der vorhergehenden Themen
verknüpft ist: Gibt es eine objektive Wirklichkeit oder kurz: Was ist Realität?
Dabei will ich nicht versuchen, dieses komplexe Thema in seiner ganzen Breite darzustellen, denn
man kann darüber leicht ganze Bücher schreiben.
Besonders die philosophischen Aspekte sollen hier nur wenig berührt werden und wir wollen
uns darauf konzentrieren, was die moderne Physik zu diesem Thema zu sagen hat.
Ganz ähnlich wie bei den Begriffen Raum und Zeit haben wir auch für die Wirklichkeit (Realität) ein unmittelbares anschauliches Verständnis, das uns im Leben begleitet. Wir glauben bereits zu wissen, was Realität ist. Doch schon bei Raum und Zeit konnten wir in den ersten Kapiteln beobachten, wie sich diese Begriffe wandeln und gar aufzulösen beginnen, wenn wir immer tiefer in sie eindringen. Ist dies bei der Realität womöglich ähnlich?
Das ist zumindest zu vermuten, denn Raum und Zeit bilden die Basis für unser intuitives Verständnis von Realität. Wenn wir uns vorstellen, dass etwas existiert, so verbinden wir normalerweise einen Ort und eine Zeit mit dieser Existenz, d.h. wir gehen von einer lokalen Realität aus, in der verschiedene Dinge an verschiedenen Orten unabhängig voneinander existieren. Wenn wir diese Grundannahme nicht machen würden, so wäre es für uns schwierig, überhaupt etwas über die Welt herauszufinden: Wenn alles mit allem eng verwoben wäre, wie könnte man dann noch Erscheinungen voneinander trennen und Ordnung ins Chaos bringen? Schließlich sind wir selbst lokal existierende Wesen und können nur die Informationen aufgreifen, die uns an unserem Ort momentan zur Verfügung stehen. Wir können die Welt nur lokal wahrnehmen!
Offenbar hängt unser Bild von der Realität eng mit unserer eigenen Wahrnehmung zusammen, und man könnte zunächst annehmen: So wie wir die Welt sehen, so ist sie auch, und was ich nicht sehen kann, gibt es auch nicht. Nun gut – diese sehr eingeschränkte Weltsicht greift ganz offensichtlich zu kurz, denn wir wissen heute, dass es sehr viele Dinge gibt, die wir nicht direkt wahrnehmen können. Wir können aber Geräte bauen, mit denen sie sich nachweisen lassen, sodass diese Geräte gleichsam unsere eingeschränkte Wahrnehmung erweitern. So können wir beispielsweise Infrarotkammeras bauen, mit denen sich die für uns unsichtbare Infrarotstrahlung sichtbar machen lässt. Realität könnte also alles das sein, was wir irgendwie messen können. Dazu müssen wir oder unser Messgerät in Wechselwirkung mit den Objekten der Welt treten: Sie müssen uns Informationen über ihre Existenz offenbaren, und oft können wir sie auch umgekehrt beeinflussen, also beispielsweise einen Gegenstand beleuchten und so sichtbar machen. Existenz bedeutet dann: You can kick it and it kicks back.
Normalerweise würden wir von einer Messung auch verlangen, dass ihr Ergebnis reproduzierbar ist. Wenn jemand anderes unter denselben Bedingungen dieselbe Messung vornimmt, sollte er auch dasselbe Messergebnis erhalten – von Messfehlern einmal abgesehen. Es sollte also egal sein, wer die Messung vornimmt, sodass wir von einer objektiven Realität ausgehen können, die unabhängig von unserer eigenen Existenz vorliegt.
Ideal wäre es, wenn wir durch Messungen tatsächlich alles über ein Objekt herausfinden könnten, was grundsätzlich an Informationen über das Objekt vorhanden ist. Dann gäbe es so etwas wie eine objektive Realität, die sich vollständig erfassen ließe, sodass Wahrnehmung bzw. Messung und Realität miteinander verschmelzen. Es gäbe keinen Unterschied mehr, da alle Aspekte der Realität offen zugänglich wären.
Wir haben also jede Menge an Erwartungen, die wir intuitiv mit dem Begriff der Realität verbinden. Schauen wir uns nun an, ob es eine solche Realität tatsächlich gibt. Man ahnt schon, dass uns da so manche Überraschung begegnen wird.
Tasten wir uns zunächst schrittweise in die Welt vor, wie sie von der klassischen Physik beschrieben wird – also der Physik, die unsere makroskopische Welt gut beschreibt, wobei man die Quantenmechanik außer Acht lässt. Klassische Physik bedeutet also für uns hier Nicht-Quanten-Physik. Was bedeutet Realität in diesem Rahmen?
Zur Zeit von Isaac Newton, also vor gut 300 Jahren, hätte man diese Frage wohl so beantworten können (auch wenn Leibniz hier nicht immer einer Meinung mit Newton war, wie wir aus den ersten Kapiteln wissen): Grundlage für die reale Welt ist ein dreidimensionaler flacher Raum sowie eine universelle Zeit, die von selbst ohne irgendeine Beeinflussung von außen fließt. Raum und Zeit bilden dabei die Bühne für die Realität, d.h. die materiellen Objekte befinden sich zu jeder Zeit immer an einem bestimmten Ort (und nehmen dort ggf. ein bestimmtes Raumvolumen ein).
Dieses Bild entspricht vollkommen unserer Anschauung, in der man sich die Elemente der Realität immer als materielle Objekte angeordnet in Raum und Zeit vorstellt, ganz nach dem Motto: Wenn sich ein stabiles reales Objekt nicht bewegt, werde ich es später an derselben Stelle wiederfinden, und wenn es sich bewegt, kann ich seine Bewegung jederzeit genau verfolgen und sie sogar mithilfe von Newtons Bewegungsgesetzen berechnen. Alle materiellen Objekte kann man dabei normalerweise sehen und meist auch anfassen, sodass sie sich für uns intuitiv als real präsentieren.
Aber schon zu Newtons Zeit war klar, dass es weitere Elemente der Realität geben muss, insbesondere das Licht, mit dessen Hilfe wir die materiellen Objekte überhaupt erst sehen können, und außerdem die Gravitation, wie sie Newton in seinem Gravitationsgesetz beschrieb. Wie passen diese beiden Phänomene in unser Bild der Realität?
Newton stellte sich Licht als Teilchenstrom vor, während andere Gelehrte eher von einer Wellenerscheinung in einer Art von materiellem Äther ausgingen, der den Raum erfüllt. Beide Vorstellungen erklären Licht durch materielle Objekte (Teilchen bzw. Ätherschwingungen) und fügen es so in das vorherrschende materiell-mechanische Bild von der Realität ein. Licht kann dann in diesem materiellen Sinn problemlos als real begriffen werden. Weiter unten werden wir sehen, dass Wellen- und Teilchenbild beide in bestimmtem Sinn zutreffen, was sich allerdings erst im Rahmen der Quantenphysik beschreiben lässt und zu einer ganz anderen Auffassung von Realität führt.
Die Gravitation passt dagegen nicht ganz so einfach in das materielle Weltbild. Offenbar gibt es sie, denn sie lässt sich eindeutig messen und auch nach Newtons Gravitationsgesetz berechnen, sodass sie in diesem Sinn real ist. Sie ist auch lokal in dem Sinn, dass man an jedem Ort die Gravitationskraft angeben kann, die auf einen kleinen Probekörper dort wirken würde. Man kann Gravitation aber nicht direkt sehen oder anfassen, sondern sie erscheint eher wie ein theoretisches Konstrukt, um die Kräfte zwischen massiven Objekten auszudrücken. Außerdem ist keinerlei Mechanismus erkennbar, der die Gravitationswirkung durch den Raum transportiert – ein Umstand, der schon Newton beunruhigte. Wir sehen also, dass unser einfaches mechanistisches Bild der Realität erweitert werden muss, um Fernwirkungen wie die Gravitation einzuschließen.
Ähnlich ist es bei den elektrischen und magnetischen Kräften. Auch hier findet man Gesetze ähnlich dem Gravitationsgesetz, um die Kräfte zwischen statischen Ladungen und Strömen zu berechnen. Aber erst die Einführung des elektrischen und magnetischen Feldes ermöglichte es, diese Kräfte übersichtlich und vor allem lokal zu beschreiben. Nun kann man die Situation nämlich begrifflich aufteilen in die Ladungen und Ströme, die ein elektromagnetisches Feld an einem bestimmten Punkt im Raum erzeugen, und die Kraft, die auf eine Probeladung oder einen Strom an diesem Punkt durch das Feld entsteht. Das Feld wirkt also wie ein Kraftübermittler. Doch ist ein solches Feld nun real, oder ist es nur eine praktische mathematische Hilfsgröße, um Kräfte zu berechnen?
Hier stoßen wir auf ein häufig wiederkehrendes Phänomen in der Physik: Sehr oft werden physikalische Begriffe eingeführt, um bestimmte Situationen geeignet zu beschreiben – auch Begriffe wie Kraft oder Masse bilden da keine Ausnahme. Wenn man aber fragt, ob Kraft oder Masse real sind, folgt zunächst oft die Antwort, das seien doch nur mathematische Hilfsgrößen. Genauso erging es dem Feldbegriff und später auch dem Atom oder dem Quark. Erst wenn nach und nach weitere Eigenschaften dieser Begriffe deutlich werden, wenn sie sich bewähren und man sich zunehmend an sie gewöhnt, dann werden sie schließlich als Elemente der Realität eingestuft. Auch bei einem so gängigen Alltagsbegriff wie Haus ist das genau genommen nicht anders: Auch ein Haus ist ein menschen-gemachter Begriff – eine Abstraktion oder Fiktion, um die Welt um uns herum zu ordnen und zu beschreiben. Das "Haus an sich", wie es sich Platon in seiner Welt der Ideen vorgestellt haben mag, gibt es nicht.
Zurück zum Feldbegriff: Im statischen Fall kann man das elektrische und magnetische Feld tatsächlich noch mit einiger Berechtigung als reine Hilfsgrößen anssehen, denn man kann die wirkenden Kräfte zwischen statischen Ladungen und Strömen auch gut ohne diese Felder beschreiben. Im dynamischen Fall ändert sich das: Veränderliche Magnetfelder erzeugen dann elektrische Wirbelfelder und umgekehrt, sodass elektromagnetische Wellen aus schwingenden Feldern entstehen können, die sich komplett von den Ladungen ablösen und vollkommen frei den leeren Raum durchqueren können. Licht ist eine solche elektromagnetische Welle, und Licht hatten wir oben durchaus als real eingestuft.
Außerdem muss man den Feldern an jedem Ort eine Energie- und Impulsdichte zuschreiben, um die Erhaltungsätze für diese Größen sicherzustellen. Licht transportiert dabei Energie und Impuls durch den Raum, ganz so wie ein materielles Objekt dies tut. Sogar das statische Feld eines geladenen Teilchens liefert mit seinem Energieinhalt einen Beitrag zur Trägheit (Masse) des Teilchens. Kurzum: Auch ein elektromagnetisches Feld besitzt Trägheit, Energie und Impuls wie eine Massenverteilung. Das Realitätskriterium You can kick it and it kicks back trifft auf elektromagnetische Felder recht gut zu. Es spricht also einiges dafür, elektromagnetische Felder als reale Bestandteile der Welt anzusehen.
Es ist sogar so, dass ein Großteil der Masse der gewöhnlichen Materie aus der Energie bestimmter Kraftfelder stammt. Protonen und Neutronen, die zusammen die Atomkerne bilden und damit den Löwenanteil der Masse von Atomen bereitstellen, bestehen nämlich aus je drei recht leichten Quarks, die von Kraftfeldern der sogenannten starken Wechselwirkung zusammengehalten werden. Dabei erzeugen die Quarks nur wenige Prozent der Masse; der Rest stammt aus der Trägheit der Kraftfelder! Wenn man Materie für real hält, so sollte man also auch diese Kraftfelder für real halten.
Die Erkenntnisse zur Realität der elektromagnetischen Felder lassen sich auch auf die Gravitation übertragen, wenn man auch diese relativistisch korrekt beschreibt, so wie Albert Einstein dies in seiner Allgemeinen Relativitätstheorie getan hat. Gravitation entspricht dann einer Krümmung von Raum und Zeit, die eine gwisse Energie-Impulsdichte besitzt und die sich ähnlich wie Licht wellenförmig fortbewegen kann (Gravitationswellen). Damit ist der Mechanismus zur Vermittlung der Gravitationswirkung, den Newton noch gesucht hatte, gefunden: Raum und Zeit selbst verändern ihre Eigenschaften und verlieren ihre Bedeutung als unveränderliche Bühne der Realität – sie werden selbst zu aktiven Beteiligten, die die Realität mit gestalten und verändern. In einer solchen Raumzeit sieht die Realität ganz anders aus, als wir das gewohnt sind – beispielsweise gibt es keine universelle Zeit mehr, die alle Beobachter in gleicher Weise wahrnehmen.
Bereits in der Speziellen Relativitätstheorie, in der die Gravitation noch gar keine Rolle spielt, verlieren Raum und Zeit ihre gewohnte Struktur, wie sie Newton noch vorschwebte – wir kennen das aus den ersten beiden Kapiteln. Gibt es deswegen gar keine Realität in Raum und Zeit mehr? Sind Raum und Zeit auch selbst keine Elemente der Realität mehr? Ist alles relativ und damit willkürlich?
Immer wieder hört man diese Ansicht, doch sie ist falsch. Die Realität sieht nur anders aus, als wir dachten! Besonders gravierend ist dabei die Relativität der Gleichzeitigkeit – oder besser: deren Beobachter-Abhängigkeit. Zwei Beobachter, die sich relativ zueinander geradlinig-gleichförmig bewegen, sehen unterschiedliche Ereignisse als gleichzeitig an. So können für den einen Beobachter zwei Sternexplosionen gleichzeitig stattfinden, während für einen anderen Beobachter diese Explosionen zeitlich nacheinander stattfinden. Auch die räumliche Entfernung zwischen den explodierenden Sternen beurteilen beide Beobachter unterschiedlich.
Was ist aber hier eigentlich noch real? Nun, man könnte den Gesamtraum aller Ereignisse in Raum und Zeit als real ansehen, also die sogenannte Raumzeit, in der jedes Ereignis seinen Platz hat und jede Geschichte eines Objektes als Raumzeit-Kurve (auch Weltlinie genannt) darstellbar ist. Alles, was irgendwann irgendwo geschieht, ist dabei ein Punkt in dieser Raumzeit, gekennzeichnet durch drei Raum- und eine Zeitkoordinate. Es ist nur so, dass relativ zueinander bewegte Beobachter die Raumzeit mit unterschiedlichen Raumzeit-Koordinatensystemen überziehen und so die Raumzeit in unterschiedlicher Weise in Gleichzeitigkeits-Scheiben zerschneiden. Eine objektive universelle Jetzt-Realität gibt es also nicht mehr. Raum und Zeit sind jeweils für sich keine objektiven Größen mehr, aber die Raumzeit lässt sich immer noch als reales Objekt begreifen, das die Bühne der Realität (also den Raum aller Ereignisse) liefert und bei Einbeziehung der Gravitation sogar selbst aktiv mitspielt, sich krümmt und so die Flugbahnen der Materie in ihr steuert.
Wie wir aus dem Kapitel Was ist Zeit wissen, ist auch der scheinbar so objektive Fluss der Zeit von der Vergangenheit in die Zukunft kein direktes Element der Realität, sondern hat letztlich sogar einen statistischen Ursprung, den man durch die Entropie quantifizieren kann. Nur weil es zu einem Zeitpunkt – dem Urknall – aus irgendwelchen Gründen einen Zustand mit sehr geringer Entropie gab, besitzt unser Universum einen eindeutig ausgerichteten Zeitpfeil, der vom Urknall aus in die Zukunft führt. Manche bezeichnen den Zeitpfeil daher auch als – wenn auch hartnäckige – Illusion, die gar kein grundlegendes Element der Realität ist, sondern sich erst aus kosmologischen Gründen herausbildet. Die grundlegenden Gesetze der Physik kennen keinen Zeitpfeil, sondern nur eine beobachter-abhängige Zeitkoordinate in der Raumzeit ähnlich einer Raumkoordinate.
Interessant ist in diesem Zusammenhang, dass das für uns sichtbare expandierende Universum dennoch einen universell gültigen Zeitstandard besitzt, den man auch als Alter des Universums und der darin befindlichen Materie bezeichnen könnte. Nur deshalb macht die Aussage "das Universum ist heute rund 13,8 Milliarden Jahre alt" überhaupt Sinn. Die Materie – also auch wir – ruht nämlich nahezu im expandierenden Raum (verglichen mit der Lichtgeschwindigkeit), wobei der Begriff ruht relatv zur kosmischen Hintergrundstrahlung definiert ist. Jeder dieser nahezu ruhenden Beobachter empfindet die Zeit nach dem Urknall und die zugehörige Entwicklung und Expansion des Universums in derselben Weise, sodass man zumindest in diesem Sinn von einer absoluten realen Zeit sprechen kann.
Bezieht man die Gravitation mit ein, so führt die dadurch hervorgerufene Krümmung von Raum und Zeit zu einem bemerkenswerten Phänomen: Es können sogenannte Ereignishorizonte auftreten. Beispielsweise umgibt uns selbst und auch jeden anderen Beobachter im expandierenden Universum ein Ereignishorizont, der sich heute in rund 16 Milliarden Lichtjahren Entfernung befindet. Explodiert heute beispielsweise ein Stern jenseits dieses Horizonts, so werden wir dies bei der heute angenommenen beschleunigten Expansion des Universums niemals sehen können, denn der Raum zwischen dem Stern und uns expandiert dann schneller, als ihn das Licht überwinden kann. Analog gibt es auch bei Schwarzen Löcher (zu einem Punkt kollabierten Sternen) einen Ereignishorizont: Ereignisse, die innerhalb dieses Horizonts stattfinden, sind von außen unsichtbar, d.h. für einen äußeren Beobachter endet die zugängliche Raumzeit am Ereignishorizont. Gibt es dann die Raumzeit jenseits des Horizonts überhaupt? Ist sie real?
Beim Ereignishorizont im beschleunigt expandierenden Universum werden die meisten Physiker ja antworten, denn ein Beobachter, der sich einige Milliarden Lichtjahre entfernt von uns befindet, kann manche der Ereignisse sehr wohl irgendwann sehen, die für uns hinter dem Horizont liegen und für immer verborgen bleiben. Jeder Beobachter hat nämlich seinen eigenen Ereignishorizont. Warum sollte die ihm zugängliche Raumzeit weniger real sein als die uns zugängliche? Es ist ähnlich wie mit dem Horizont auf unserer Erdkugel: Hinter dem Horizont geht es weiter, und jeder sieht einen anderen Ausschnitt der Erdoberfläche.
Ist das mit dem Ereignishorizont bei Schwarzen Löchern genauso? Hier ist es etwas schwieriger, denn für alle außen stehenden Beobachter bleibt die Raumzeit innerhalb des Ereignishorizonts verborgen und die Zeit bleibt am Ereignishorizont stehen. Allerdings könnte man sich in das Schwarze Loch hineinfallen lassen und so den Ereignishorizont überwinden. Nach Einsteins Allgemeiner Relativitätstheorie sollte man beim Überqueren des Ereignishorizonts nichts besonderes verspüren – man kann nur ab diesem Moment keine Signale mehr in die Außenwelt schicken und wird unvermeidlich ins Zentrum des Schwarzen Lochs stürzen. Für einen solchen frei fallenden Beobachter wäre der Raum innerhalb des Ereignishorizonts also real, und wieder können wir fragen, warum seine Realität weniger wert sein soll als unsere. Außerdem ist die Raumzeit innerhalb des Ereignishorizonts ein unvermeidlicher Bestandteil der theoretischen Beschreibung Schwarzer Löcher in der Allgemeinen Relativitätstheorie, d.h. in der Theorie existiert auch die Raumzeit innerhalb des Ereignishorizonts und ist Bestandteil der gesamten Raumzeit. Wir werden weiter unten noch einmal auf dieses Thema zurückkommen – dann allerdings unter Einbeziehung der Quantenmechanik.
Fassen wir noch einmal zusammen, was Realität in der klassischen Welt ohne Quanten bedeutet: Die physikalische Beschreibung der Realität beruht auf dem Raum der Ereignisse, also der Raumzeit, die die Bühne für Materie und Kraftfelder liefert. Bei Einbeziehung der Gravitation wird auch die Raumzeit selbst zum aktiven Mitspieler und kann sich krümmen und verzerren. Raum und Zeit selbst sind Beobachter-abhängige Größen – man spricht manchmal auch von der vielfingerigen Zeit – wobei das sichtbare Universum einen objektiven Zeitstandard besitzt. Materie und Kraftfelder können wir ebenfalls beide als real bezeichnen, zumal auch Felder Energie und Impuls sowie Trägheit besitzen und man Materie oft auch als lokal eingesperrtes Kraftfeld verstehen kann (man denke an das starke Kraftfeld zwischen den Quarks im Proton, das den größten Teil der Protonmasse erzeugt).
Was bestimmt nun die physikalischen Eigenschaften von Raum und Zeit, Materie und Kraftfeldern? Bei den Kraftfeldern beantworten die entsprechenden Feldgleichungen diese Frage, beispielsweise die Maxwellgleichungen, die das elektromagnetische Feld mit den elektrischen Ladungs- und Stromverteilungen in Raum und Zeit verknüpfen. Auch bei der Gravitation gibt es ähnliche Gleichungen: Hier verbinden die Einsteingleichungen die Krümmung der Raumzeit mit der Energie-Impulsverteilung der Materie im Raum, wobei auch Massen zur Energieverteilung beitragen (man denke an \( E = m c^2 \) ).
Doch was bestimmt die Eigenschaften der Materie? Woraus besteht Materie? Ist Materie kontinuierlich und mit ihren Eigenschaften eben einfach da, oder gibt es tiefer liegende Ebenen der Realität?
Heute wissen wir, dass die zweite Möglichkeit in der Natur realisiert ist: Materie besteht aus Atomen, die wiederum fast komplett aus leerem Raum bestehen (in dem gewisse Quantenwellen schwingen). Die scheinbar so solide Materie ist genau genommen ein sehr luftiges Gespinst, und tatsächlich gibt es bestimmte Teilchen (die Neutrinos), für die Materie kaum ein Hindernis darstellt, denn sie durchfliegen ohne größere Probleme sogar die komplette Erde. Auch wenn uns selbst Materie so fest und robust vorkommt, so besteht sie in der Realität doch hauptsächlich aus viel leerem Raum.
Als sich die Indizien für die atomare Struktur der Materie zunehmend häuften,
stieß diese Idee oft auf erbitterten Widerstand, denn sie widerspricht unserer
intuitiven Auffassung, wie Materie real aussieht. Oft wurden Atome als
eine nützliches, aber rein theoretisches Konstrukt angesehen, das man zwar zur Beschreibung
bestimmter Phänomene gut gebrauchen kann, dem aber keine Realität zukommt.
Noch um das Jahr 1900 fragte der bekannte
österreichische Physiker Ernst Mach bei der Erwähnung von Atomen
schnippisch:
"Ham se welche gesehen?"

Quelle:
Wikimedia Commons File:Ernst Mach 01.jpg, dort public domain;
aus Zeitschrift für Physikalische Chemie, Band 40, von 1902
Tatsächlich glaubte man lange Zeit, Atome seien zu klein, um sie jemals
sehen zu können, doch wie so oft hat man die technische Entwicklung unterschätzt.
Mit modernen Raster-Tunnelmikroskopen gelingt es heute tatsächlich, Atome
zu sehen oder besser: Sie mithilfe einer extrem feinen Spitze und etwas
elektrischem Strom zu erfühlen, wie das folgende Bild zeigt:

Quelle:
Wikimedia Commons File:Graphite ambient STM.jpg, dort public domain;
Frank Trixler, Ludwig-Maximilians-Universität München (LMU);
adapted from LMU/CeNS: Organic Semiconductor Group
Ein solches Bild lässt jeden Zweifel verstummen und Atome gelten heute als vollkommen reale Bestandteile der Welt, ebenso wie die Bausteine (Elektronen, Protonen und Neutronen), aus denen sie bestehen, denn auch diese Bausteine lassen sich meist direkt sichtbar machen, beispielsweise als Teilchenspuren in Detektoren.
Als man jedoch bei Protonen und Neutronen auf die Suche nach deren Bestandteilen ging und die Hypothese aufstellte, dass diese aus Quarks bestehen, wiederholte sich das bekannte Spiel: Quarks galten zunächst als rein mathematisches Modell, mit dem sich zwar die Vielfalt der sogenannten Hadronen (zu denen auch Protonen und Neutronen gehören) näherungsweise erklären ließ, die aber keineswegs realen Teilchen entsprachen. Tatsächlich gelang es bis zum heutigen Tag nicht, auch nur ein einzelnes freies Quark nachzuweisen, sodass man sich tatsächlich fragen kann, ob Quarks reale Teilchen sein können. Allerdings gelang es, die Quarks im Inneren der Protonen und Neutronen durch Streuexperimente indirekt nachzuweisen, so wie auch Rutherford die Existenz von Atomkernen im Zentrum der Atome durch Streuung von Alphateilchen an ihnen nachgewiesen hatte. Wenn man nämlich sehr energiereiche Elektronen ins Innere eines Protons schießt, so werden sie von den Quarks darin in typischer Weise aus ihrer Bahn geworfen – man leuchtet gleichsam das Innere des Protons mit hochenergetischen Elektronen aus und macht so die Quarks darin indirekt sichtbar. Heute werden Quarks daher als real existierende Teilchen akzeptiert, auch wenn man davon ausgeht, dass Quarks nie als freie Teilchen existieren können – man spricht hier vom Confinement.
Ein Grund dafür, warum sich die Quarks trotz Confinements als Teilchen nachweisen lassen, liegt darin, dass sie der elektromagnetischen und der starken Wechselwirkung unterliegen, sodass sie wirkungsvoll mit anderer Materie in Kontakt treten können – nur deshalb sind Streuexperimente mit ihnen so gut machbar. Es gibt aber auch Teilchen, die weder elektrisch geladen sind noch der starken Wechselwirkung unterliegen: die nahezu masselosen Neutrinos. Sie spüren neben der Gravitation nur die sogenannte schwache Wechselwirkung, die nur eine extrem kurze Reichweite hat. Neutrinos müssen also einem anderen Teilchen sehr nahe kommen, damit die schwache Wechselwirkung wirken kann. Daher nennt man Neutrinos auch Geisterteilchen. Sie können beispielsweise die gesamte Erde fast ungestört durchfliegen – nur ganz selten kommt es dabei zu Wechselwirkungen zwischen einem Neutrino und einem Atomkern.
Neutrinos sind also in gewissem Sinn gerade noch real, wie der Begriff Geisterteilchen zeigt. Zugleich gehören sie neben den Photonen der kosmischen Hintergrundstrahlung zu den häufigsten Teilchen im Universum. Die meisten von ihnen sind in den ersten Sekunden nach dem Urknall entstanden und bilden heute eine kosmische Neutrino-Hintergrundstrahlung, mit rund 300 Neutrinos pro Kubikzentimeter (siehe auch Wikipedia: Kosmischer Neutrinohintergrund). Diese Neutrinos fliegen fast mit Lichtgeschwindigkeit und befinden sich überall im Raum – auch in jedem Kubikzentimeter unseres eigenen Körpers. Dennoch merken wir nichts von ihnen, denn die Temperatur dieser Neutrinos liegt bei nur rund zwei Kelvin, also noch unterhalb der Temperatur der Photonen-Hintergrundstrahlung von 2,7 Kelvin. Sie haben daher eine so geringe Energie, dass es bis heute als nahezu aussichtslos erscheint, sie jemals direkt nachzuweisen – nur hochenergetische Neutrinos, wie sie beispielsweise bei radioaktiven Zerfällen entstehen, lassen sich bis heute in riesigen Detektoren aufspüren. Kosmologische Beobachtungen und theoretische Berechnungen liefern aber viele indirekte Hinweise auf die zahlreichen kosmischen Niederenergie-Neutrinos, sodass heute niemand an ihrer Existenz zweifelt. Auch ohne direkten Nachweis kann also ein Objekt in der Physik als real gelten, solange es messbare indirekte Auswirkungen hat, die gut mit zugehörigen theoretischen Vorstellungen übereinstimmen.
Auch der allererste Hinweis auf Neutrinos war indirekt: Beim radioaktiven Betazerfall schienen Energie und Impuls verloren zu gehen, und man zweifelte schon an der Gültigkeit der Energie-Impuls-Erhaltung. Dem österreichischen Physiker Wolfgang Pauli gefiel das überhaupt nicht – zu gut hatten sich diese Erhaltungssätze bisher bewährt. In einem berühmt gewordenen Brief aus dem Jahr 1930 an eine Physiker-Tagung in Tübingen schlug er deshalb die Existenz eines elektrisch neutralen Teilchens vor, das beim Betazerfall zusätzlich entsteht und unerkannt entkommt, wobei es die scheinbar fehlenden Energie- und Impulsbeträge mit sich fortträgt:
"Liebe Radioaktive Damen und Herren,
Wie der Überbringer dieser Zeilen, den ich huldvollst anzuhören bitte, Ihnen des näheren auseinandersetzen wird, bin ich angesichts der falschen Statistik der N- und Li-6 Kerne, sowie des kontinuierlichen beta-Spektrums auf einen verzweifelten Ausweg verfallen um den Wechselsatz der Statistik und den Energiesatz zu retten. Nämlich die Möglichkeit, es könnten elektrisch neutrale Teilchen, die ich Neutronen nennen will, in den Kernen existieren, welche den Spin 1/2 haben und das Ausschließungsprinzip befolgen und sich von Lichtquanten außerdem noch dadurch unterscheiden, dass sie nicht mit Lichtgeschwindigkeit laufen. Die Masse der Neutronen könnte von der gleichen Größenordnung wie die Elektronenmasse sein und jedenfalls nicht größer als 0,01 Protonenmassen. Das kontinuierliche beta-Spektrum wäre dann verständlich unter der Annahme, dass beim beta-Zerfall mit dem Elektron jeweils noch ein Neutron emittiert wird, derart, dass die Summe der Energien von Neutron und Elektron konstant ist."
(siehe z.B.
ETH Zürich).

Quelle:
Wikimedia Commons File:Pauli.jpg, dort public domain;
Nobel foundation
Pauli nannte sie noch Neutronen, gemeint waren aber die Neutrinos, wie sie heute genannt werden (Neutronen sind ja die neutralen Kernbausteine). Außerdem wissen wir heute, dass – anders als Pauli noch annahm – diese Teilchen fast mit Lichtgeschwindigkeit laufen und dass ihre Ruhemasse sehr viel kleiner als die Elektronenmasse ist. Wichtig ist an dem Brief vor allem, dass Pauli von einem verzweifelten Ausweg spricht, denn Pauli zweifelte daran, dass sich sein neues Teilchen überhaupt im Experiment nachweisen ließ. So sagte er später (siehe z.B. Wolfgang Pauli – Leben und Werk von Wolfgang Steinicke, Umkirch):
"Heute habe ich etwas Schreckliches getan, etwas, was kein theoretischer Physiker jemals tun sollte. Ich habe etwas vorgeschlagen, was nie experimentell verifiziert werden kann."
Wie real ist so ein Teilchen, das man zwar braucht, um die Energie-Impuls-Erhaltung zu retten, das man aber womöglich nie direkt nachweisen kann? Zum Glück erwiesen sich Paulis Bedenken als unbegründet, denn im Jahr 1956 – also 26 Jahre nach Paulis Brief – gelang der direkte Nachweis des Neutrinos.
Auch heute ist man auf der Jagd nach Teilchen, die es aus verschiedenen Gründen geben könnte. Ein bekanntes Beispiel ist das berühmte Higgs-Teilchen (auch etwas reißerisch als Gottesteilchen bezeichnet), dessen Existenz schon in den Jahren 1964 bis 1968 zur Erklärung der Teilchenmassen im Standardmodell der Teilchenphysik gefordert wurde, das aber erst im Sommer 2012 nachgewiesen werden konnte. Ähnlich ist es bei den noch unbekannten Teilchen der dunklen Materie: Es gibt mittlerweile jede Menge Indizien für die Existenz dieser dunklen Materie, sodass kaum jemand daran zweifelt, dass sie Teil der Realität sein muss. Bisher (Stand 2023) verrät sie sich jedoch allein durch ihre Gravitationswirkung im Universum – ein direkter Nachweis steht noch aus.
Manchmal gibt es in der Physik aber auch Teilchen, über deren reale Existenz man nun wirklich geteilter Meinung sein kann. Ein bekanntes Beispiel sind die Fadeev-Popov-Geistteilchen (oder auch Geistfelder) in der Quantenchromodynamik QCD (das ist die Theorie, die die starke Wechselwirkung beschreibt, welche beispielsweise die Quarks zu Protonen und Neutronen zusammenschweißt). Aus mathematischen Gründen benötigt man in der QCD diese Geistteilchen, wobei diese zwar zwischen Quarks und Gluonen hin- und herpendeln können, aber nie als selbstständige Teilchen frei werden oder als Streuzentren ähnlich wie Quarks wirken können. Hier hat man tatsächlich den Eindruck, dass es sich um rein mathematische Hilfsterme in einer komplizierten Theorie handelt – doch Vorsicht: auch bei den Quarks und sogar bei Atomen war man einmal dieser Ansicht!
Fassen wir unsere bisherigen Erkenntnisse noch einmal zusammen: Woraus besteht die Wirklichkeit aus der Sicht der klassischen Physik? Sie besteht aus Materie und Kraftfeldern oder besser: Aus Teilchen und Wechselwirkungsfeldern in der (ggf. gekrümmten) Raumzeit. Dabei durchlaufen die Teilchen im Lauf der Zeit eine Bahn im Raum, wobei die Wechselwirkungsfelder die Kräfte zwischen den Teilchen vermitteln und dabei auch selbst Energie und Impuls besitzen.
War es das? Haben wir damit die Realität tatsächlich physikalisch erfasst? Weit gefehlt, wie uns der nun folgende Abschnitt zeigen wird.
Das bisher skizzierte Bild der Realität kann sehr vieles erklären. Und dennoch wurde spätestens im beginnenden zwanzigsten Jahrhundert immer klarer, dass dieses Bild Lücken aufweist: Warum stürzen die Elektronen der Atomhülle nicht in den Atomkern, obwohl sie doch als kreisende Ladungen wie in einer Antenne ständig Energie abstrahlen müssten? Warum kann Licht beim Photoeffekt aus einer Alkalimetall-Oberfläche im Vakuum Elektronen herausschlagen, so als ob es aus einem Strom von Teilchen bestünde und nicht aus einer elektromagnetischen Welle? Warum können die Wände in einem Ofen ihre Energie immer nur in bestimmten Energieprotionen an das Wärme-Strahlungsfeld abgeben?
Einige dieser Fragen hatten wir bereits in den vorhergehenden Kapiteln angesprochen und auch schon gesehen, wie die Antwort lautet: Teilchen wie beispielsweise Elektronen bewegen sich gar nicht auf Teilchenbahnen, sondern Teilchenbahnen sind nur eine Näherung, so wie ein Lichtstrahl nur eine Näherung für die Lichtausbreitung im Raum ist. In Wahrheit bewegen sich hier Wellen durch den Raum, wobei die Intensität der Welle an einem Ort für die Wahrscheinlichkeit steht, ein Teilchen dort anzutreffen. Man muss dafür allerdings auch aktiv nachsehen, also den Teilchenort konkret messen, um das Teilchen dazu zu zwingen, sich für einen Ort zu entscheiden. Ohne eine solche Ortsmessung ist der Teilchenort unbestimmt – das Elektron weiß gewissermaßen selbst nicht, wo es sich aufhält, und es muss das auch gar nicht wissen. Der Ort des Elektrons spielt nämlich beispielsweise für die Physik der Atomhülle gar keine Rolle, sondern die Elektronenwelle ist es, deren Schwingungen hier entscheidend sind.
Was bedeutet diese merkwürdige Situation nun für unser Verständnis der Realität? Sind Elektronen denn nun Teilchen oder sind sie Wellen? In unserem intuitiven Realitätsverständnis schließen sich beide Beschreibungen gegenseitig aus: Teilchen haben einen definierten Ort und bewegen sich auf einer Flugbahn, während Wellen so wie auch Felder im Raum verschmiert sind, wobei sich die Wellenamplitude an jedem Ort mit der Zeit ändern kann.
Nun benimmt sich ein Elektron in einer Atomhülle wie eine stehende Welle, während es sich bei einer Ortsmessung wie ein Teilchen mit zufällig gewähltem Ort und unbestimmter Geschwindigkeit verhält. Beim Photoeffekt erscheint es dagegen wie ein Teilchen mit bestimmter Geschwindigkeit (abhängig von der Wellenlänge), aber mit weitgehend unbestimmtem Ort.
Dieses merkwürdige Verhalten wird oft unter dem Begriff Welle-Teilchen-Dualistmus zusammengefasst: Erst das Experiment bestimmt demnach darüber, ob ein Elektron als Welle oder als Teilchen in Erscheinung tritt, wobei Ort und Geschwindigkeit nicht gleichzeitig festliegen können (Unschärferelation). Eine unabhängige Realität scheint es dann aber nicht mehr zu geben, wenn erst das Experiment über die Natur des Elektrons entscheidet. Außerdem liegen weder Ort noch Geschwindigkeit des Elektrons vor der Messung in der Natur fest: Man kann zeigen, dass beispielsweise bei einer Ortsmessung die Ortsinformation erst im Moment der Messung entsteht und nicht etwa vorher schon im Verborgenen vorhanden ist (Stichwort Bellsche Ungleichung, siehe auch unten). Albert Einstein konnte sich mit diesem Verlust einer wohlbestimmten Realität nie anfreunden, wie sein berühmter Ausspruch Gott würfelt nicht zeigt.
Gott scheint also bei einer Ortsmessung den Ort des Elektrons sehr wohl zu würfeln. Die gesamten real vorhandenen Eigenschaften des Elektrons stecken laut Quantenmechanik in seiner Wellenfunktion (also in der Elektronenwelle), und deren Intensität an einem Ort ist nun einmal lediglich die Wahrscheinlichkeit dafür, das Teilchen dort zu finden. Mehr Realität ist offenbar nicht vorhanden. Ist damit die Wellenfunktion womöglich das entscheidende Element der Realität? Besteht die Realität aus Wellenfunktionen?
Man könnte das vermuten, doch es gibt ein Problem: Vor einer Ortsmessung ist eine Wellenfunktion normalerweise über einen Raumbereich verteilt. Doch direkt nach der Ortsmessung weiß man ja, wo das Elektron sich befindet. Würde man den Ort unmittelbar nach der Ortsmessung ein zweites Mal bestimmen, so muss nahezu wieder derselbe Ort herauskommen. Die Wellenfunktion direkt nach der ersten Ortsmessung muss dabei die Wahrscheinlichkeiten für die zweite Ortsmessung korrekt widerspiegeln, d.h. sie ist nun ein scharfer Peak am gemessenen Ort des Elektrons, die erst im Lauf der Zeit wieder auseinanderlaufen kann – man spricht vom Kollaps der Wellenfunktion.
Die erste Ortsmessung lässt also blitzartig die Wellenfunktion auf einen Punkt kollabieren. Das wäre kein Problem, wenn wir die Wellenfunktion als rein mathematische Darstellung der jeweils vorhandenen Information interpretieren. Die vorhandene Information hat sich durch die Messung eben spontan verändert, und mit ihr auch die Wellenfunktion. Manche Physiker halten diese Gleichsetzung von Information und Realität für die Lösung aller Probleme, doch man wird das Gefühl nicht los, dass hier etwas nicht ganz stimmt: Information über was? Über eine Realität? Welche?
Wenn wir nun aber die Wellenfunktion als physikalisches Element der Realität interpretieren, dann dürfen wir eine Messung nicht mehr als reinen Informationsgewinn ansehen, sondern wir müssen sie als physikalischen Prozess beschreiben, der letztlich zum Kollaps der Wellenfunktion führt. Das Problem ist nur: In der Quantentheorie existiert kein Mechanismus, der einen solchen Kollaps hervorrufen kann. Steht damit der Messprozess außerhalb der Quantentheorie? Das wäre sehr merkwürdig, denn es spricht heute alles dafür, dass die Quantentheorie die universelle Beschreibung unserer Natur darstellt, und dass die klassische Welt, wie wir sie wahrnehmen, sich erst als Näherung aus der Quantentheorie ergibt.
Erst in den letzten Jahren hat sich in ersten Ansätzen eine mögliche Lösung des Messproblems herauskristallisiert, auch wenn sich hierzu keineswegs schon eine einheitliche Meinung unter den Physikerinnen und Physikern herausgebildet hat. Das Thema bleibt umstritten, aber ich will diesen Lösungsansatz hier dennoch skizzieren, da er sich ohne jede Zusatzannahme vollkommen im etablierten Rahmen der Quantentheorie bewegt, auch wenn die Konsequenzen für die Realität ziemlich bizarr sind.
Die Grundidee ist folgende: Das oben dargestellte Bild einer Elektron-Wellenfunktion im Raum ist nur ein Spezialfall in der Quantenmechanik. Allgemein muss man Teilchen, die miteinander wechselwirken oder dies irgendwann einmal getan haben, durch eine einzige gemeinsame Wellenfunktion beschreiben. Diese befindet sich nicht im gewöhnlichen dreidimensionalen Raum und gibt darin die Ortswahrscheinlichkeit für ein einziges Teilchen an, sondern sie lebt im sogenannten Konfigurationsraum. Für ein System aus mehreren Teilchen wäre das beispielsweise ein Raum mit drei Ortskoordinaten für jedes Teilchen und noch einem Bitwert für den Teilchenspin. Für jede Wertekombination der Orte und Spins aller Teilchen zusammen hat die Wellenfunktion einen bestimmten Wert, dessen Betragsquadrat die Wahrscheinlichkeit dafür angibt, diese Wertekombination bei einer dazu passenden Messung vorzufinden.
Der Konfigurationsraum ist also letztlich der Raum aller Messwertkombinationen, die sich bei einem physikalischen System gleichzeitig messen lassen. Bei einem makroskopischen Objekt mit 1020 Teilchen hätte dieser Raum also 3 mal 1020 Ortskordinaten plus 1020 Spinkordinaten und wäre dementsprechend extrem hochdimensional. Niemand wird die zugehörige Wellenfunktion jemals berechnen oder messen können, aber dennoch sollte es sie im Prinzip geben.
In einfachen Fällen mit nur wenigen verschränkten Teilchen lassen sich Konfigurationsraum und Wellenfunktion dagegen oft angeben. Dabei tritt der merkwürdige Effekt der Verschränkung klar zu Tage. Das bekannteste Beispiel sind zwei Teilchen mit Spin 1/2, die von einer Teilchenquelle in entgegengesetzte Richtungen ausgesendet werden und die zusammen den Gesamtspin Null besitzen. Der Konfigurationsraum besteht hier aus den beiden Teilchenpositionen und den beiden Spinkomponenten (Spinorientierungen).
Laufen die Teilchen nun jeweils durch ein
senkrecht orientiertes inhomogenes Magnetfeld, so werden sie je nach Spinorientierung
entweder nach oben oder nach unten abgelenkt – man sagt, sie haben die Spinkomponente
+1/2 oder −1/2. Da sich zusammen immer Spin Null ergeben muss, gehört zu einem Teilchen
mit Spinkomponente +1/2 ein Partnerteilchen mit Spinkomponente −1/2
und umgekehrt,
d.h. die Teilchen verhalten sich in dem Magnetfeld entgegengesetzt zueinander:
Wird ein Teilchen nach oben abgelenkt, so wird das Partnerteilchen nach unten abgelenkt
und umgekehrt.
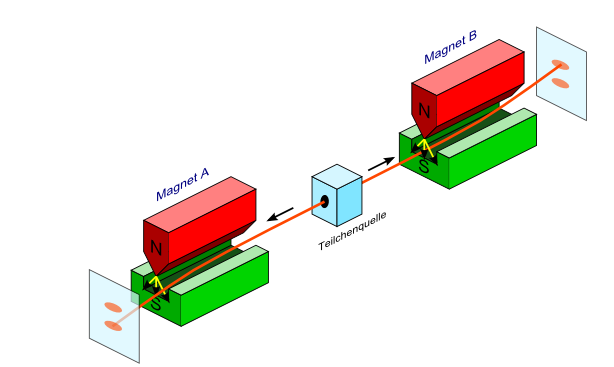
Nun können die beiden Teilchen prinzipiell Lichtjahre voneinander entfernt sein, bevor sie auf das Magnetfeld treffen. Sie haben dann keine Chance mehr, ihr Verhalten erst jetzt aufeinander abzustimmen, denn dafür müssten sie Informationen mit Überlichtgeschwindigkeit austauschen, was nach Albert Einsteins Relativitätstheorie unmöglich ist. Albert Einstein schloss daraus, dass die beiden Teilchen bereits vorher ihre Spins aufeinander abgestimmt haben müssen und ihre jeweilige Spinorientierung als innere Teilcheninformation mit sich tragen. Diese innere Teilcheninformation, in der die Spinkomponente jedes Teilchens fest vorgegeben ist, gibt es aber in der Quantenmechanik bei dem Teilchenpaar nicht – dort existiert nur die Wellenfunktion, die das Verhalten beider Teilchen gemeinsam beschreibt, nicht aber das Verhalten jedes Teilchens für sich. Die Quantenmechanik sagt nur, dass sich die beiden Spinkomponenten entgegengesetzt zueinander verhalten, sagt aber nicht, welche Spinkomponente das einzelne Teilchen trägt. Einstein schloss daraus – zusammen mit Rosen und Podolsky – dass die Quantenmechanik unvollständig sein müsse, denn in ihr fehlt beispielsweise der Teilchenspin als Variable, die jedem Teilchen einzeln zugeordnet ist. Ganz analog ist es auch bei dem Teilchenort oder dem Teilchenimpuls. Diese Variablen seien in der Quantenmechanik verborgen und würden erst in einer fundamentaleren Theorie erscheinen, die der Quantenmechanik zugrunde liegt.
Bei diesen Überlegungen macht Einstein eine wichtige Voraussetzung, die uns selbstverständlich erscheint. In seinem Text Quanten-Mechanik und Wirklichkeit drückt er es folgendermaßen aus:
"Fragt man, was unabhängig von der Quanten-Theorie für die physikalische Ideenwelt characteristisch ist, so fällt zunächst folgendes auf: die Begriffe der Physik beziehen sich auf eine reale Außenwelt, d. h. es sind Ideen von Dingen gesetzt, die eine von den wahrnehmenden Subjekten unabhängige "reale Existenz" beanspruchen (Körper, Felder, etc.), welche Ideen andererseits zu Sinneseindrucken in moglichst sichere Beziehung gebracht sind. Characteristisch für diese physikalischen Dinge ist ferner, dass sie in ein raum-zeitliches Kontinuum eingeordnet gedacht sind. Wesentlich für diese Einordnung der in der Physik eingeführten Dinge erscheint ferner, dass zu einer bestimmten Zeit diese Dinge eine voneinander unabhängige Existenz beanspruchen, soweit diese Dinge "in verschiedenen Teilen des Raumes liegen". Ohne die Annahme einer solchen Unabhängigkeit der Existenz (des "So-Seins") der räumlich distanten Dinge voneinander, die zunächst dem Alltags-Denken entstammt, wäre physikalisches Denken in dem uns geläufigen Sinne nicht möglich. Man sieht ohne solche saubere Sonderung auch nicht, wie physikalische Gesetze formuliert und geprüft werden könnten. Die Feldtheorie hat dieses Prinzip zum Extrem durchgeführt, indem sie die ihr zugrunde gelegten voneinander unabhängig existierenden elementaren Dinge sowie die für sie postulierten Elementargesetze in den unendlich-kleinen Raum-Elementen (vierdimensional) lokalisiert.
Für die relative Unabhängigkeit räumlich distanter Dinge (A und B) ist die Idee characteristisch: äußere Beeinflussung von A hat keinen unmittelbaren Einfluss auf B; dies ist als "Prinzip der Nahewirkung" bekannt, das nur in der Feld-Theorie konsequent angewendet ist. Völlige Aufhebung dieses Grundsatzes würde die Idee von der Existenz (quasi-) abgeschlossener Systeme und damit die Aufstellung empirisch prüfbarer Gesetze in dem uns geläufigen Sinne unmöglich machen."
Einstein nahm also an, dass beide Teilchen eigenständige Elemente der Realität sind, zumal wenn sie sich womöglich Lichtjahre voneniander entfernt befinden. Die Quantenmechanik behandelt sie jedoch als untrennbare Einheit, egal wie weit sie voneinander entfernt sind – sie sind nur gemeinsam ein Element der Realität.
Im Jahr 1964 konnte John Steward Bell zur Überraschung vieler Physiker zeigen, dass das statistische Verhalten der beiden Teilchen in zueinander verdrehten Magnetfeldern davon abhängt, ob ein verborgener innerer Teilchenspin lokal pro Teilchen existiert oder nicht. Gäbe es diesen inneren Teilchenspin, so würden sich die Teilchen anders verhalten als von der Quantenmechanik vorhergesagt. Nun stimmt aber die Quantenmechanik mit sehr großer Genauigkeit mit allen Experimenten überein – keine einzige Abweichung konnte bisher trotz intensiver Suche entdeckt werden. Damit ist Einsteins Annahme einer lokalen Realität widerlegt. Schade, dass Eintein selbst die Überlegungen von Bell nicht mehr erleben konnte.
In der Quantenmechanik verlieren die einzelnen Teilchen also ihre lokale Eigenständigkeit: Nur gemeinsam sind sie ein Element der Realität, beschrieben durch die gemeinsame Wellenfuntion. Die Teilchen sind miteinander verschränkt, d.h. nur über das Gesamtverhalten aller Teilchen lässt sich noch eine umfassende Aussage machen, nicht aber über das Verhalten eines einzelnen Teilchens (genauer: man verliert Information, wenn man nur Aussagen über einzelne Teilchen macht). Wenn das die Realität sein soll, dann ist sie hochgradig nichtlokal, denn die Teilchen können weit voneinander entfernt sein und sind dennoch nicht einzeln vollständig beschreibbar.
Nun haben letztlich seit dem Urknall alle Teilchen des Universums, die sich innerhalb des sogenannten Teilchenhorizonts (heute ca. 45 Milliarden Lichtjahre) befinden, irgendwann einmal einander beeinflusst. Man kann also vermuten, dass alles, was wir im Universum sehen oder messen können, durch eine einzige gemeinsame Universums-Wellenfunktion beschrieben werden muss, die sich in einem geradezu monströs-hochdimensionalen Konfigurationsraum bewegt. Ist diese Wellenfunktion die Realität?
Wenn ja, dann ist sie uns nicht zugänglich. Dass dies so sein muss, kommt bereits in dem obigen Text von Albert Einstein zu Ausdruck, wenn er dort schreibt:
"Ohne die Annahme einer solchen Unabhängigkeit der Existenz (des "So-Seins") der räumlich distanten Dinge voneinander, die zunächst dem Alltags-Denken entstammt, wäre physikalisches Denken in dem uns geläufigen Sinne nicht möglich."
Genau so ist es: die gesamte Quanten-Wirklichkeit mit ihren globalen Verschränkungen quer durch das Universum können wir weder wahrnehmen noch messen. Man kann sich zwar eine theoretische Vogelperspektive vorstellen, aus der heraus ein göttliches Wesen diese Wellenfunktion komplett überblickt, die alle Teile des Universums miteinander verbindet und verschränkt. Da wir selbst aber lokale Wesen sind, die irgendwie als Teil dieser universellen Wellenfunktion existieren und keinerlei Zugang zu all den globalen Verschränkungen des Universums haben, bleibt uns diese Realität grundsätzlich verborgen. Wir sitzen gleichsam in einer Froschperspektive gefangen und können nur einen winzigen Aussschnitt der Quanten-Realität sehen, der über lokale Wechselwirkungen zugänglich ist und sich uns als klassische Realität präsentiert.
Wie muss man sich in dieser Welt nun die Ortsmessung bei einem Elektron vorstellen? Nun, zunächst einmal muss das Elektron derart in einen bestimmten Zustand versetzt worden sein, dass man es in sehr guter Näherung als eigenständiges Quantensystem durch eine eigene Wellenfunktion beschreiben kann, weitgehend entkoppelt vom Rest des Universums (der Umgebung). Insbesondere darf es dabei keine Wechselwirkung mit der Umgebung haben, die makroskopisch messbare Spuren im restlichen Universum hinterlässt. Nun kommt die Ortsmessung: Dazu muss man das Elektron in eine Wechselwirkung mit der makroskopischen Umgebung bringen, die sehr empfindlich auf den Ort des Elektrons reagiert und je nach Ort zu einer Veränderung in der Umgebung führt, an der man makroskopisch die einzelnen Orte unterscheiden kann. Die Orte der anderen Teilchen in der Umgebung – beispielsweise die Teilchen im Zeiger eines Messgeräts – werden also mit dem zu messenden Ort unseres Elektrons verschränkt, so dass ihr Ort vom zu messenden Elektron-Ort abhängt. Die Umgebung (und letztlich das gesamte Universum inklusive uns selbst) und das Elektron müssen nun wieder durch eine gemeinsame Wellenfunktion beschrieben werden.
Wie sieht diese gemeinsame Wellenfunktion aus? Sie enthält verschiedene Anteile (Zweige), und zwar einen für jeden möglichen Elektronenort plus Umgebung (wobei man eine gewisse Genauigkeit vorgeben muss, sodass nur endlich viele Elektronenorte makroskopisch unterschieden werden können). Dabei sind Umgebung und Elektronenort so miteinander verschränkt, dass verschiedene Elektronenorte zu verschiedenen makroskopisch unterscheidbaren Umgebungen gehören – beispielsweise zu verschiedenen Zeigerstellungen an einem Messgerät.
Wie groß ist diese Umgebung? Letzten Endes gehört das gesamte Universum dazu, also insbesondere auch wir Menschen, denn auch wir sind über unzählige winzige Wechselwirkungen beispielsweise mit der Zeigerstellung und somit mit dem gemessenen Elektronenort verschränkt – nur deshalb können wir die Zeigerstellung überhaupt sehen.
Nun existiert aber für jeden möglichen Elektronenort ein Zweig der Universums-Wellenfunktion, in dem die Umgebung (der Zeiger des Messgeräts) diesen Elektronenort makroskopisch anzeigt und wir Menschen ihn entsprechend als gemessen wahrnehmen. Keiner dieser Zweige ist realer als die anderen Zweige, und jeder dieser Zweige enthält gleichsam eine Kopie der gesamten makroskopisch wahrnehmbaren Realität einschließlich aller Menschen, nur mit jeweils anderem gemessenen Elektronenort. Die makroskopische Realität hat sich gewissermaßen aufgespalten, wobei jeder Elektronenort seinen eigenen Zweig bekommen hat. Und genau das geschieht jedes Mal, wenn aus einer Quanten-Möglichkeit eine makroskopische Gewissheit wird, also in jeder Sekunde unzählige Male. Es entsteht das bizarre Bild eines universellen Quanten-Universums, in dem sich ständig unzählige neue Zweige einer makroskopisch unterschiedlichen Realität bilden. Auch wir selbst verzweigen uns dabei ständig, und von jedem von uns entstehen unentwegt neue Kopien in eigenen makroskopischen Welten – ein wirklich bizarrer Gedanke!
Doch warum merken die unterschiedlichen Zweige nichts mehr voneinander, wenn sie sich erst einmal voneinander getrennt haben? Grundsätzlich könnten sie einander durchaus noch beeinflussen, denn sie sind ja alle Teile derselben Universums-Wellenfunktion. Und dennoch begegnet uns niemals eine solche abgezweigte Kopie von uns selbst. Das liegt daran, dass im Moment der Messung eine sehr schnelle Dekohärenz der verschiedenen Anteile der Wellenfunktion stattfindet. Dadurch, dass das Elektron bei der Messung seines Ortes mit den unzähligen Freiheitsgraden der makroskopischen Welt verschränkt wird, geraten die verschiedenen Zweige mit den verschiedenen Elektronenorten gleichsam aus dem Takt und können einander nicht mehr so überlagern, dass das makroskopisch und vor allem lokal wahrnehmbar wäre. In jedem dieser Zweige sehen die darin enthaltenen Menschen einen anderen Elektronenort, der wie zufällig gewählt erscheint, da alle anderen Elektronenorte mit ihren Zweigen unerreichbar in den Tiefen des Konfigurationsraums entschwunden sind. Es sieht dabei in jedem Zweig so aus, als sei die Wellenfunktion des Elektrons auf einen zufälligen Punkt kollabiert, weil man in jedem der Zweige die anderen Anteile der Elektron-Wellenfunktion mit den nun zugehörigen Umgebungs-Anteilen nicht mehr sieht. Da die Dekohärenz extrem schnell abläuft, scheint dieser Kollaps sprungartig zu erfolgen – der berühmte Quantensprung. In Wahrheit gibt es – zumindest wenn man dieser Argumentation folgt – gar keinen Quantensprung, sondern die universelle Wellenfunktion entwickelt sich gemäß der linearen Schrödingergleichung stetig weiter, wobei die verschiedenen makroskopischen Zweige wegen der unzähligen beteiligten Freiheitsgrade (die Umgebung) sehr schnell dekohärieren und sich so makroskopisch trennen.
Die verschiedenen Zweige existieren dabei alle gleichberechtigt weiter, nur in verschiedenen Bereichen des Konfigurationsraums. Man kann sich das grob so wie bei einem Radiosender vorstellen, der zunächst gleichzeitig zwei verschiedene Lieder im selben Frequenzband spielt, sodass wir beide zugleich in einem Radioempfänger hören können, der auf dieses Frequenzband eingestellt ist. Diese Überlagerung der Lieder im selben Frequenzband entspricht der quantenmechanischen Überlagerung verschiedener Elektronenorte. Plötzlich geht nun der Sender dazu über, das Frequenzband in zwei verschiedene Frequenzbänder aufzuspalten und in jedem dieser Frequenzbänder nur eines der beiden Lieder abzuspielen. Zugleich verdoppeln wir den Radioempfänger, wobei nun jeder der beiden Empfänger nur auf eines der beiden Frequenzbänder eingestellt ist. Es sind zwar immer noch zugleich beide Lieder in den elektromagnetischen Wellen des Senders vorhanden, aber jeder Empfänger ist nur für eines der Bänder empfindlich und hört auch nur noch ein Lied.
Die obige Beschreibung des Messprozesses wird oft als Viele-Welten-Interpretation der Quantenmechanik bezeichnet. Dabei greift der Begriff Interpretation etwas zu kurz, denn wir haben uns lediglich angesehen, welche Folgen es hat, wenn man die Quantenmechanik als universell gültige Theorie auch für die makroskopische Welt akzeptiert und in diesem Rahmen auch den Messprozess physikalisch beschreibt. Dabei spielt der Begriff der Dekohärenz eine entscheidende Rolle, denn durch ihn trennen sich die verschiedenen Zweige der universellen Wellenfunktion ständig in einzelne neue Zweige auf, die makroskopisch unabhängigen Realitäten entsprechen, so wie wir sie als lokale Wesen aus unserer Froschperspektive heraus messen und wahrnehmen können, während uns der Zugang zur gesamten Quanten-Realität (der Wellenfunktion des Universums mit all ihren Zweigen) versperrt bleibt.
Auf diese Weise gelingt es, eine konsistente Quanten-Beschreibung des gesamten Universums zu erreichen, wie sie beispielsweise Claus Kiefer in seinem Buch Der Quantenkosmos: Von der zeitlosen Welt zum expandierenden Universum verwendet (übrigens sehr empfehlenswert!). Es gibt darin keine künstliche Trennung zwischen klassischer Welt und Quantenwelt mehr, und auch der Messprozess selbst lässt sich physikalisch beschreiben. Zudem muss man nicht auf eine mikroskopische Realität verzichten, wie dies bei klassischen Interpretationen der Quantenmechanik der Fall ist (siehe oben). Es gibt nämlich eine übergreifende Quanten-Realität, auch wenn wir selbst immer nur einen Zweig davon sehen.
Der Preis dafür ist allerdings hoch, und nicht jeder ist heute schon bereit, ihn zu bezahlen: Da ständig überall Dekohärenzprozesse stattfinden, entstehen im Quantenkosmos in jedem Moment unzählige neue Zweige der Wellenfunktion, die unabhängigen klassischen Realitäten entsprechen, wobei wir selbst uns dabei mitverzweigen. Was soll man davon halten, dass sich das eigene Ich unablässig vervielfältigt? Wenn man jedoch uns selbst als makroskopischen Teil des Universums im Rahmen einer Quantenwelt begreift, dann unterliegen auch wir selbst natürlich den physikalischen Gesetzen. Dabei bleibt das Bild konsistent, denn jedes der neu entstandenen Ichs sieht nur sich selbst (nicht aber seine Kopien), besitzt eine Erinnerung an die Vergangenheit und würde schwören, das Elektron bei der Messung an dem entsprechenden Ort vorgefunden zu haben, der zu seinem Realitätszweig gehört.
Kann diese bizarre Welt tatsächlich die Realität sein? Kaum zu glauben! Doch unsere intuitive Abneigung gegen bestimmte Ideen ist meist ein schlechter Ratgeber, wenn es um die Beantwortung physikalischer Fragen geht – aus Sicht der Quantenmechanik spricht durchaus einiges dafür, dass das beschriebene Bild die wahre Natur der Quanten-Realität korrekt darstellen könnte, auch wenn diese eine geradezu barocke Vielfalt gleichzeitig existierender klassischer Realitätszweige umfasst.
Interessanterweise gibt es in diesem Bild gar keine Teilchen (und auch keine Kraftfelder) mehr, denn das einzige Element der Realität ist die Wellenfunktion des Universums. Bei der Messung des Elektronenorts sieht es in jedem Zweig der Wellenfunktion lediglich so aus, als würde sich ein Elektron an einem bestimmten Ort zeigen. In Wahrheit bildet sich hier aber aufgrund einer lokalen Wechselwirkung eine Verschränkung zwischen Elektronen-Wellenfunktion und der Wellenfunktion der Umgebung, und erst die Dekohärenz zwischen den verschiedenen Zweigen lässt es in jedem Zweig so aussehen, als hätte man das Elektron an einem Ort gemessen, wobei die Ortsgenauigkeit dieser Messung durch die (sehr kleine) sogenannte Kohärenzlänge gegeben ist (die gemessenen Elektronenorte in verschiedenen Zweigen der universellen Wellenfunktion müssen weiter als die Kohärenzlänge auseinanderliegen, damit die Zweige durch Dekohärenz auch getrennt werden und damit separaten klassischen Realitäten entsprechen). Die Dekohärenz lässt also Quantenwellen wie Teilchen erscheinen, wobei die maximale Genauigkeit der Ortsmessung der bei der Messung verbleibenden Kohärenzlänge entspricht.
Dazu passt, dass der Begriff des Teilchenorts nur in der nichtrelativistischen Quantenmechanik überhaupt eine klar definierte Rolle als Messgröße spielt: Nur dort ist das Betragsquadrat der Wellenfunktion die Wahrscheinlichkeitsdichte dafür, ein Teilchen am entsprechenden Ort zu finden. In der relativistischen Quantenfeldtheorie ist das nicht mehr so! Der Teilchenort hat hier nur noch eine diffuse, ungenaue Bedeutung und spielt für die Physik auch streng genommen keine Rolle mehr. So macht die Frage "Wo befindet sich ein Photon?" nur noch sehr eingeschränkt Sinn.
In der relativistischen Quantenfeldtheorie gibt es weder reale Teilchen noch reale Kraftfelder, sondern nur noch eine Wellenfunktionen in einem hochdimensionalen Konfigurationsraum, der beispielsweise auch die Amplituden der Felder umfasst – wobei auch dies wohl nur eine Näherung ist, denn den wirklichen Konfigurationsraum, in dem die Wellenfunktion lebt, kennen wir noch gar nicht. Wenn wir nach der fundamentalen physikalischen Theorie (der Weltformel) suchen, so suchen wir letztlich nach diesem Konfigurationsraum und den Gesetzen, welche die Wellenfunktion unseres Universums darin formen. Nach den Regeln der Quantengravitation ist die Wellenfunktion unseres Universums dabei sogar zeitlos, und nur unter speziellen Bedingungen lässt sich überhaupt noch ein approximativer Zeitbegriff definieren, wie wir im Kapitel über die Zeit gesehen haben.
Es ist durchaus möglich, dass es Wellenfunktionen (Quantenfelder) gibt, die wegen ihrer sehr schwachen Wechselwirkung mit dem Rest der Welt nie dekohärieren, sich also nie als lokale Teilchen zeigen und so zur Bildung neuer Realitätszweige führen. Die geheimnisvolle Dunkle Energie könnte ein solches Quantenfeld sein. Sie lässt über ihre gravitative Abstoßung zwar nach heutigem Wissen unser Universum zunehmend schneller expandieren, doch kennt man ansonsten bisher keine weitere Wechselwirkung zwischen Dunkler Energie und der sonstigen Materie. Womöglich reicht die lokal so schwache Gravitation nicht aus, dass hinreichende Dekohärenz entsteht und sich Dunkle Energie -Teilchen zeigen – die Kohärenzlänge wäre für teilchenartige Effekte zu lang. Auch bei der Gravitation selbst könnte es dieses Phänomen geben: Das berühmte Graviton wäre demnach nur eine Fiktion, das sich nie als lokales Teilchen nachweisen ließe.
Schon bei Neutrinos ist es schwierig, sie als Teilchen nachzuweisen, denn auch die Schwache Wechselwirkung genügt nur selten, um genügend Dekohärenz zu erzeugen – Neutrinos sind auch deshalb Geisterteilchen. Die schwache Dekohärenz ermöglicht es andererseits, bei Neutrinos typische Quanteneffekte auch über makroskopische Distanzen hinweg aufzuspüren, da diese nicht durch Dekohärenz zerstört werden. Die berühmten Neutrino-Oszillationen sind genau ein solcher Quanteneffekt. So werden in der Sonne sogenannte Elektron-Neutrino-Quantenwellen erzeugt, die sich als quantenmechanische Überlagerung dreier Wellen mit verschiedener Masse und verschiedener Wellenlänge verstehen lassen. Die Überlagerung dieser Wellen verändert sich daher beim Durchqueren des Raums, sodass sie auf der Erde einer Überlagerung von Elektron-, Myon- und Tauon-Neutrinowellen entsprechen. Bei entsprechender Wechselwirkung mit Materie können daher nicht nur Elektron-Neutrinos nachgewiesen werden, sondern auch Myon- und Tauon-Neutrinos, obwohl man in der Sonne nur Elektron-Neutrinos hätte finden können. Bei Neutrinos können also über astronomische Distanzen hinweg quantenmechanische Überlagerungen verschiedener Neutrino-Flavors und verschiedener Neutrino-Massen überleben, da keine Dekohärenz stattfindet – weder die Massen noch die Flavors werden auf dem Weg von der Sonne zu uns gewissermaßen gemessen; sie verschränken sich also nicht mit dem Rest des Universums.
Bei geladenen freien Teilchen ist eine solche langlebige Quanten-Überlagerung undenkbar. Die elektrische Ladung führt ständig zu derart intensiver Wechselwirkung mit der Umgebung, dass Ladung und Masse dieser Teilchen praktisch ständig gemessen wird. Daher gibt es keine quantenmechanische Überlagerung eines Elektrons mit einem Proton, bei der man beispielsweise eine 50-zu-50-Chance hätte, entweder ein Elektron oder ein Proton bei einer Messung vorzufinden. Eine solche Überlagerung – wenn sie sich überhaupt erzeugen ließe – würde sofort dekohärieren und man hätte einen Realitätszweig mit dem Elektron und einen Zweig mit dem Proton. Das nennt man in der Quantenmechanik Superauswahlregeln.
Interessanterweise können sich innerhalb eines Hadrons (Protonen und Neutronen gehören dazu) durchaus Quarks mit verschiedenen elektrischen Ladungen quantenmechanisch überlagern, solange die Gesamtladung des Hadrons bei jeder Überlagerungskomponente dieselbe ist. So besteht das elektrisch neutrale Pion aus einer quantenmechanischen Überlagerung eines up-antiup- und eines down-antidown Quark-Antiquark-Paares, wobei das up-Quark die Ladung +2/3 und das down-Quark die Ladung −1/3 besitzt (die Antiquarks haben jeweils die entgegengesetzte Ladung). Da sich die Ladungen von Quark und Antiquark gegenseitig neutralisieren und beide im Pion eng beisammen sitzen, wird nur die Gesamtladung des Pions – also Null – von der Außenwelt wahrgenommen und die Überlagerung ist stabil gegen Dekohärenz. Man kann also gar nicht eindeutig sagen, aus welchem Quark-Antiquark-Paar (up-antiup oder down-antidown) das neutrale Pion besteht – es enthält beides zugleich. Ganz ähnlich überlagern sich in einem Hadron übrigens auch die verschiedenen Farbladungswerte der Quarks, die die starke Wechselwirkung repräsentieren, denn das Hadron besitzt nach außen die Farbladung Null.
Mit dem Teilchenbegriff ist das also in der Quantentheorie so eine Sache, und folgt man der Viele-Welten-Interpretation, dann sind Teilchen gar keine realen Objekte, sondern sie werden durch die Dekohärenz vorgetäuscht. Besonders deutlich wird dies, wenn man den sogenannten Unruh-Effekt betrachtet (wobei dieser Effekt unabhängig von der Viele-Welten-Interpretation ist):
Wenn ein Beobachter im ansonsten leeren Raum – dem Vakuum – ruht oder sich geradling-gleichförmig darin bewegt, gibt es für diesen Beobachter keinerlei Teilchen im Raum. Es gibt beispielsweise keinerlei Photonen-Treffer aus dem Vakuum auf einer empfindlichen Photoplatte. Genau das soll ja der Begriff Vakuum auch aussagen. Quantenmechanisch wird das Vakuum durch einen komplexen Quantenzustand beschrieben, der alle erreichbaren Teile des Raums miteinander verschränkt. Dieser Quantenzustand ist vollkommen statisch, verändert sich also zeitlich nicht. Man stellt sich zwar oft das Quanten-Vakuum als fluktuierenden See virtueller Teilchen vor, doch das ist nur ein anschauliches Hilfbild, mit dem sich Wechselwirkungen zwischen Vakuum und Materie darstellen lassen.
Beschleunigt dagegen ein Beobachter im leeren Raum, so nimmt er im Prinzip eine – wenn auch extrem kalte und schwache – Teilchen-Wärmestrahlung wahr, die aus seiner Sicht das Vakuum erfüllt. Das Vakuum erscheint nun wie das Innere eines (sehr kalten) Ofens, der umso heißer wird, je größer die Beschleunigung ist. Experimentell nachgewiesen ist dieser Effekt zwar noch nicht, doch theoretische Rechnungen legen es sehr nahe, dass er existiert.
Wie aber kann es sein, dass der unbeschleunigte Beobachter keine Teilchen im Raum sieht, der beschleunigte Beobachter dagegen schon? Man kann diesen Effekt als weiteres Indiz dafür deuten, dass Teilchen keine fundamentalen Elemente der Realität sind. Es ist vielmehr so, dass sich für beide Beobachter das Vakuum in einem unterschiedlichen Quantenzustand befindet. Während nämlich für den unbeschleunigten Beobachter der gesamte Raum zugänglich ist und damit zum Vakuum-Quantenzustand gehört (die Expansion des Universums lassen wir hier außer Acht), existiert für den beschleunigten Beobachter ein Ereignishorizont: Das Licht von Ereignissen, die weit genug hinter ihm stattfinden, wird ihn niemals erreichen, wenn er konstant weiterbeschleunigt. Der Teil des Raums außerhalb des Ereignishorizontes ist also für den konstant beschleunigten Beobachter unzugänglich und gehört demnach auch nicht zu seinem Vakuum-Quantenzustand hinzu. Dieser veränderte Quantenzustand macht sich für ihn durch eine sehr schwache Wärme-Teilchenstrahlung bemerkbar.
Stellt man sich das Vakuum behelfmäßig wieder als fluktuierenden See virtueller Teilchen vor, so trennt der Ereignishorizont virtuelle Teilchen-Antiteilchen-Paare voneinander, sodass sich diese nicht wieder gegenseitig vernichten, was sie ohne Ereignishorizont tun würden. Allerdings täuscht dieses Bild eine objektive Teilchen-Realität vor, die es nicht gibt, denn nur der beschleunigte Beobachter sieht ja einen Ereignishorizont – der Ereignishorizont ist also gar kein Beobachter-unabhängiges Element der Realität, und ebensowenig kann das dann die Entstehung von Teilchen durch Trennung von ihren Antiteilchen sein.
Existiert für einen Beobachter ein Ereignishorizont, so führt dies ganz allgemein zu einer schwachen Wärme-Teilchenstrahlung für diesen Beobachter, denn so stellt sich für ihn der entsprechende Vakuum-Quantenzustand dar. Daher muss auch der Ereignishorizont des expandierenden Universums, der das für uns sichtbare Universum begrenzt, zu einer solchen Wärmestrahlung führen. Allerdings ist diese Strahlung so extrem schwach, dass man sie wohl niemals wird aufspüren können.
Am geläufigsten sind die Ereignishorizonte schwarzer Löcher – wir sind ihnen oben bereits begegnet.
Der Raum innerhalb eines solchen Ereignishorizontes ist für einen weit außen
ruhenden Beobachter unzugänglich, und entsprechend nimmt der äußere Beobachter
eine sehr schwache Wärmestrahlung wahr, die vom Ereignishorizont des schwarzen Lochs ausgeht:
die sogenannte Hawking-Strahlung.
Ein in das schwarze Loch hineinfallender Beobachter wird dagegen keine Hawking-Strahlung sehen,
denn für ihn existiert der Ereignishorizont nicht und sein freier Fall neutralisiert
aus seiner Sicht die Gravitation.
Ein frei fallender Beobachter entspricht nämlich nach Einsteins
Äquivalenzprinzip einem ruhenden Beobachter im gravitationsfreien Raum:
Wenn man frei fällt, spürt man die Gravitation nicht mehr.
Der frei fallende Beobachter bemerkt am Ereignishorizont
also nichts besonderes und fällt schließlich unaufhaltsam
ins Zentrum des schwarzen Lochs.
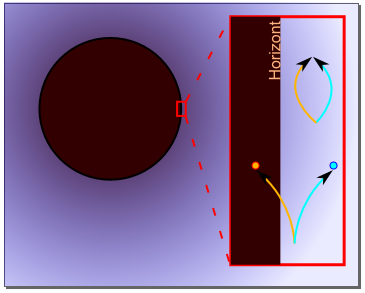
Wie sieht ein außenstehender Beobachter dieses Hineinfallen des anderen Beobachters? Nach Einsteins Allgemeiner Relativitätstheorie wird er das Hineinfallen nie beobachten, da aus seiner Sicht die Zeit zum Ereignishorizont hin immer langsamer läuft und am Horizont sogar stehen bleibt. Die Fallbewegung und überhaupt jeder physikalische Vorgang im fallenden Objekt scheinen einzufrieren, und das von ihm ausgesendete Licht wird immer energieärmer, bis es nicht mehr messbar ist. Damit entgleitet das fallende Objekt aus der zugänglichen Realität des außenstehenden Beobachters – es verblasst gewissermaßen.
Nimmt man die Quantenphysik hinzu, so könnte die Situation sich aus Sicht des äußeren Beobachters womöglich noch deutlich dramatischer darstellen (ausgearbeitet u.a. von Susskind und 't Hooft, siehe z.B. Wikipedia: Black hole complementarity). Die schwache Hawking-Wärmestrahlung, die von weit außen gesehen vom Ereignishorizint des schwarzen Lochs ausgeht, ist nämlich nur deshalb schwach, weil sie auf ihrem Weg zum äußeren Beobachter gegen die starke Gravitation ankämpfen muss und dabei viel Energie verliert. Am Ereignishorizont selbst muss sie dagegen sehr energiereich sein und aus Sicht des äußeren Beobachters alles zerstören, was in ihre Nähe kommt. Demnach wird das hinabfallende Objekt kurz über dem Ereignishorizont von der dort herrschenden starken Strahlung vollkommen zerlegt und mitsamt der in ihm vorhandenen Information über den gesamten Ereignishorizont verteilt. Von dort wird die Materie des zerstörten Objekts dann mitsamt all seiner Information als Hawking-Strahlung sehr langsam wieder hinaus ins Universum abgestrahlt. Die in ihm gespeicherte Information geht also nicht verloren – was ein Grundpostulat der Quantenmechanik ist – , wird allerdings für jeden praktischen Zweck unbrauchbar. Die Welt hinter dem Ereignishorizont wird dabei zu keiner Zeit betreten. Aus Sicht des äußeren Beobachters gibt es diesen inneren Bereich praktisch nicht, sondern das schwarze Loch selbst besteht nur aus dem Ereignishorizont, über den sich seine gesamte Masse gleichmäßig verteilt und sehr langsam als Hawking-Strahlung wieder abgestrahlt wird. Daher ist es auch gut verständlich, dass beispielsweise die Entropie eines Schwarzen Lochs, die normalerweise mit dem Volumen eines Systems skaliert, proportional zu dessen Ereignishorizontfläche anwächst und nicht proportional zum Raumvolumen innerhalb des Ereignishorizonts.
Der hinabfallende Beobachter kann dagegen den inneren Bereich jenseits des Ereignishorizonts problemlos betreten. Für ihn extistiert dieser Bereich also, auch wenn er ihn aus eigener Sicht niemals wieder verlassen kann. Bei seinem Sturz würde er am Ereignishorizont keinerlei Strahlung sehen, denn er spürt als frei fallendes Objekt weder die Gravitation noch den Ereignishorizont. Daher würde er vollkommen intakt mitsamt all seiner Information weiter hinabstürzen und nur die starken Gezeitenkräfte könnten ihn unterwegs zerreißen.
Was aber ist nun real? Das was der äußere Beobachter sieht oder das, was der hinabfallende Beobachter empfindet? Wird der fallende Beobachter nun am Ereignishorizont zerlegt oder nicht? Möglicherweise bilden sich auch hier zwei Realitätszweige in der universellen Wellenfunktion, die einander zunächst zu widersprechen scheinen. Allerdings hat dieser Widerspruch keine Chance, sich jemals in einem einzigen Realitätszweig zu manifestieren, denn die beiden Zweige werden nie wieder zusammenfinden. Es wird nie einen makroskopischen Beobachter geben, der beide Realitäten zugleich bestätigen kann, denn der hinabfallende Beobachter wird nie wieder aus dem schwarzen Loch auftauchen können, um zu beweisen, dass er nicht zerlegt wurde. Was nun aber die richtige Realität ist, kann man nicht sagen – beides sind nur dekohärente Zweige in einer universellen Wellenfunktion, die zugleich beide Möglichkeiten umfasst. Diese Wellenfunktion kann aber von keinem klassischen lokalen Beobachter jemals in ihrer Gesamtheit überblickt werden, denn diese Beobachter sind immer Teil ihres eigenen Realitätszweiges.
Die Realität ist also keineswegs so einfach, wie unsere Intuition uns glauben lässt. Hat bereits die Relativitätstheorie unsere Anschauung von Raum und Zeit strapaziert, so hat spätestens die Quantenmechanik ganz grundsätzlich die Frage aufgeworfen, was Realität eigentlich sein soll. Gibt es sie überhaupt auf mikroskopischer Ebene noch? Müssen wir uns womöglich mit dem Gedanken an eine universellen Wellenfunktion anfreunden, die unzählige Realitätszweige umfasst? Es ist noch zu früh, auf diese Fragen eine endgültige Antwort zu geben. Die Diskussionen sind noch in vollem Gang, und bisher ist nach wie vor Richard Feynman's berühmter Satz "Niemand versteht die Quantenmechanik" gültig. Erst wenn wir hier einen Schritt weiter kommen und insbesondere den Prozess der Messung besser verstehen, wird es uns gelingen, auch dem Rätsel der Realität weiter auf den Grund zu gehen. Ob uns das jemals in vollem Unfang gelingt, bleibt abzuwarten, aber es gibt gerade in letzter Zeit sehr ermutigende Entwicklungen (Stichwort Dekohärenz), die zeigen, dass hier Fortschritt durchaus möglich ist.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 17 February 2023