Kapitel 2
Was ist Raum?

Über die Definition des Raums
Inertialsysteme und Relativitätsprinzip
Der Raum in der speziellen Relativitätstheorie
Sind die Naturgesetze spiegelsymmetrisch?
Gekrümmte Räume
Die Gravitation krümmt Raum und Zeit
Die Raumzeit des Universums
Die Zahl der Raumdimensionen
Der Quantenraum

"Der Raum ist die Ordnung gleichzeitig existierender Dinge, wie die Zeit die Ordnung des Aufeinanderfolgenden."
Gottfried Wilhelm Leibniz (Brief v. 16.6.1712 an B. des Bosses, Philos. Schr. II, 450)

Wie bei der Zeit haben wir Menschen auch für den Raum ein gewisses intuitives Verständnis. Wir wissen scheinbar von Natur aus, was Raum und Zeit sind, und können uns eine Welt ohne Raum und Zeit überhaupt nicht vorstellen. Dies veranlasste beispielsweise den deutschen Philosophen Immanuel Kant in seiner Kritik der reinen Vernunft um das Jahr 1781 zu der Ansicht, Raum und Zeit seinen unabdingbare (a priori) Voraussetzungen unserer Wahrnehmung und damit unabhängig und vor aller Erfahrung. Raum und Zeit sind demnach keine Eigenschaften der Welt, die wir an ihr entdecken, sondern wir benötigen sie als unverzichtbaren Rahmen, um die Welt überhaupt begrifflich erfassen zu können.

Doch ist das tatsächlich schon alles, was über den Raum gesagt werden kann? Das Beispiel der Zeit hat uns im letzten Kapitel bereits gezeigt, wie komplex und tiefgründig dieser Begriff wird, wenn wir ihn im Licht der modernen Physik betrachten, und wie sehr er sich dabei von unserem intuitiven Empfinden zu entfernen beginnt. Der Verdacht liegt nahe, dass es sich mit dem Raum ebenso verhalten könnte. Es lohnt sich also, aus dem Blickwinkel der Physik genauer hinzuschauen!

Über die Definition des Raums

Wie bei so vielen physikalischen Begriffen tun wir uns mit einer exakten Definition wieder einmal schwer – dies zeigt schon der obige Definitionsversuch von Immanuel Kant, der sich alleine auf unsere menschliche Erkenntnisfähigkeit bezieht, die ohne Raum und Zeit nicht auszukommen scheint.

Der englische Physiker Isaac Newton war einer der ersten, der um das Jahr 1687 versucht hat, den Begriff des Raumes genauer zu spezifizieren. Er kam zu dem Schluss, dass es einen absoluten und unveränderlichen Raum gibt, der gleichsam die Bühne für die sich darin abspielenden physikalischen Vorgänge liefert, ohne dabei selbst beeinflusst zu werden. Dieser Raum ist nach Newton euklidisch (also ungekrümmt bzw. "flach") und besitzt drei Dimensionen.

Wie schon bei Newtons Zeitdefinition entspricht auch seine Raumdefinition unserer intuitiven Vorstellung. Außerdem enthält sie zusätzlich einige mathematische Details, liefert also ein konkretes mathematisches Raummodell:

• Der Raum soll dreidimensional und kontinuierlich sein, d.h. wir benötigen drei reelle Zahlen, um die Koordinaten eines jeden Punktes darin anzugeben.

• Der Raum soll euklidisch sein, d.h. man kann in diesem Raum über Abstände und Winkel reden, und man kann den kompletten Raum lückenlos mit einem rechtwinkligen (karthesischen) verzerrungsfreien Koordinatensystem überziehen. In einem solchen Raum beträgt beispielsweise die Winkelsumme in einem Dreieck immer 180 Grad.

Beide Eigenschaften sind keineswegs selbstverständlich, wie wir weiter unten noch sehen werden.

Newtons Zeitgenosse, der deutsche Mathematiker und Philosoph Gottfried Wilhelm Leibniz, kam analog zur Zeit auch beim Raum zu einer anderen Überzeugung: Wie unser Eingangszitat zu Beginn dieses Kapitels zeigt, gab es für Leibniz keinen unabhängig existierenden Raum. Er sah den Raum lediglich als ein gedankliches Hilfsmittel an, um Abstände und Winkel zwischen Objekten und deren Verbindungslinien beschreiben zu können. Einen absolut leeren Raum ohne irgendwelche Objekte darin kann es nach Leibniz nicht geben.

Eine ähnliche Meinung vertrat später auch der österreichische Physiker und Philosoph Ernst Mach. Nach seinem Mach'schen Prinzip macht es keinen Sinn, von der Bewegung eines Körpers gegenüber dem absoluten Raum zu sprechen. Man kann die Bewegung immer nur relativ zu den anderen Objekten – beispielsweise den Sternen und Galaxien im Weltall – angeben. Damit hatte Mach großen Einfluss auf Albert Einstein – mehr dazu später.

Wer hat nun recht – Newton oder Leibniz bzw. Mach? Gibt es den Raum als real existierendes Element der Wirklichkeit, oder ist er nur ein gedankliches Konstrukt?

Das ist schwer zu sagen, denn physikalische Begriffe bilden immer eine gedankliche Abstraktion, die dazu dient, unsere physikalischen Beobachtungen zu strukturieren und ein mathematisch-physikalisches Modell der Realität zu entwerfen.

Ähnliche Diskussionen kennt man auch von anderen physikalischen Begriffen. Ist beispielsweise ein elektromagnetisches Feld etwas real Existierendes, oder ist es lediglich ein hilfreiches mathematisches Konstrukt, um die elektromagnetischen Kräfte zwischen geladenen Objekten elegant lokal beschreiben zu können? Wenn man elektrischen und magnetischen Phänomenen zum ersten Mal begegnet, neigt man meist der zweiten Möglichkeit zu, denn ein elektromagnetisches Feld erscheint einem wenig greifbar zu sein, während man geladene Objekte gleichsam "anfassen" kann. Steigt man dann tiefer ein, so erkennt man, dass ein elektromagnetisches Feld Energie und Impuls besitzt – ganz wie ein reales Objekt. Nimmt man noch die Erkenntnisse der Quantenmechanik hinzu, so kommt der Begriff des Photons ins Spiel und ersetzt den Begriff des Feldes. Photonen sind aber ebenso real wie Elektronen oder Protonen!

Wir müssen uns also der Frage nach dem Raumes physikalisch nähern: Welche Naturgesetze gelten in Bezug auf den Raum, und was sagen sie über die physikalische Natur des Raums aus?

Um in der Physik überhaupt über den Raum sprechen zu können, braucht man natürlich eine passende physikalische Messvorschrift, also ein Abstands- oder Längenmaß. Das heutige Standardmaß für Längen, der Meter, wurde ursprünglich im Jahr 1793 vom französische Nationalkonvent als der zehnmillionsten Teil der Entfernung vom Nordpol über Paris zum Äquator definiert. Im Jahr 1799 goss man einen entsprechenden Platinstab – den Urmeter, und bewahrte diesen unter genau kontrollierten Bedingungen sorgfältig auf. Als man später die Gestalt der Erde genauer vermessen konnte, erwies sich dieser Platinstab als nur 0,02 % zu kurz. Dennoch behielt man ihn als Repräsentant der Maßeinheit Meter bei, sodass die Entfernung vom Nordpol zum Äquator über Paris nun 10001,966 km lang war.

Natürlich ist weder die Gestalt der Erde noch ein Platinstab in der Lage, den heutigen Anforderungen an die Genauigkeit und Reproduzierbarkeit einer Maßeinheit zu genügen. Wie soll man beispielsweise erkennen, wenn der Urmeterstab seine Länge geringfügig ändert, da er doch selbst den Vergleichsmaßstab für alle anderen Längen definiert?

Viel besser ist es daher, unveränderliche Naturkonstanten zu verwenden, um eine Maßeinheit zu definieren. Bei der Sekunde war es eine bestimmte Schwingungsfrequenz in Atomen, die diesen Naturstandard lieferte. Genauso machte man es schließlich auch beim Meter: Im Jahr 1960 definierte man den Meter als ein bestimmtes Vielfaches der Wellenlänge einer Strahlung, die gewisse Atome aussenden – ganz ähnlich wie bei der Sekunde. Das tat man natürlich so, dass man dabei die Länge des Urmeter-Platinstabs so genau wie möglich reproduzierte.

Seit 1983 hat man eine noch bessere Definition gefunden: Ein Meter ist seitdem die Strecke, die Licht im Vakuum innerhalb von 1 / 299 792 458 Sekunden durchläuft. Mit anderen Worten: Die Lichtgeschwindigkeit hat seitdem den festen Wert von 299 792 458 Metern pro Sekunde und dient dazu, die Längeneinheit Meter aus der Zeiteinheit Sekunde abzuleiten. Der krumme Zahlenwert ist wieder dem Umstand geschuldet, dass man möglichst wenig von der zuvor gültigen Meterdefinition abweichen wollte. Einfacher wäre es gewesen, die Längeneinheit Lichtsekunde zu verwenden, also die Strecke, die das Licht in einer Sekunde zurücklegt. Das wäre für den täglichen Gebrauch aber wohl doch zu unhandlich gewesen.

Die heutige Meter-Definition passt sehr gut zu unserer Erkenntnis aus der speziellen Relativitätstheorie, dass Licht für jeden gleichförmig bewegten oder ruhenden Beobachter immer genau dieselbe Geschwindigkeit hat – wir kennen das bereits aus dem letzten Kapitel und gehen weiter unten noch einmal genauer darauf ein. Daher bietet sich diese Naturkonstante geradezu an, um aus ihr eine Maßeinheit abzuleiten. Analog versucht man heute, auch andere Naturkonstanten für die Definition von Maßeinheiten zu verwenden, beispielsweise das Planck'sche Wirkungsquantum aus der Quantenmechanik. Das ist nicht immer einfach, denn eine Maßeinheit muss sich ja auch problemlos und präzise in einem Labor reproduzieren lassen, um als Vergleichsmaßstab für eine Messung dienen zu können. Aktuell gibt es große Anstrengungen, beispielsweise das Kilogramm auf Naturkonstanten zurückzuführen und endlich vom Urkilogramm – einem Platin-Iridium-Zylinder – loszukommen, der analog zum früheren Urmeter bis heute diese Maßeinheit festlegt.

Inertialsysteme und Relativitätsprinzip

Isaac Newton brachte als einer der Ersten ein physikalisches Argument ins Spiel, um seinen Standpunkt eines absoluten und unveränderlichen Raumes zu untermauern: Er betrachtete einen wassergefüllten Eimer, der drehbar an einem Seil befestigt wird. Nun wird der Eimer in eine gleichmäßige Drehung um die Senkrechte gebracht, wobei sich das Wasser nach einiger Zeit synchron mit dem Eimer mitdreht. Dabei steigt die Wasseroberfläche aufgrund der Fliehkraft zum Rand hin an, während sie ohne die Rotation eine ebene Fläche bildet. Man kann also alleine an der Wasseroberfläche erkennen, ob sich Eimer und Wasser um eine senkrechte Achse drehen oder nicht. Dabei benötigt man keinerlei Bezug zu irgendwelchen Objekten jenseits des Eimers, um die Stärke der Rotation zu ermitteln. Man kann also mit Fug und Recht von einer absoluten Rotation des Eimers sprechen – oder wenn man so will von einer Rotation des Eimers gegenüber dem absoluten Raum.

Ernst Mach hat gegenüber Newtons Argument eingewendet, der Eimer bewege sich ja gar nicht in einem absolut leeren Raum. In der Realität existiert im Universum jede Menge Materie, die erst das Bezugssystem definiert, gegenüber dem sich der Eimer dreht. Diese Materie müsse irgendeinen Einfluss auf den Eimer haben und so den Anstieg des Wassers am Rand des Eimers hervorrufen, wenn dieser sich gegenüber der Materie des Universums dreht. Mach war also strikt der Meinung, jede Bewegung könne nur relativ zu anderen Körpern angegeben werden, auch eine beschleunigte Bewegung wie beispielsweise eine Drehbewegung. Damit hat Mach ein extrem weitgehendes Relativitätsprinzip formuliert – ob es sich wohl in der Realität bewährt?

Wenn man dieses Relativitätsprinzip auf geradlinig-gleichförmige Bewegungen einschränkt, so gilt es bereits in der klassischen Mechanik, wie sie Isaac Newton formuliert hat: Alle sich geradlinig-gleichförmig bewegenden Bezugssysteme – sogenannte Inertialsysteme – sind physikalisch gleichwertig, d.h. man kann ganz im Sinne von Ernst Mach nur relative Bewegungen zwischen ihnen feststellen, aber keine absoluten Bewegungen. Es gibt in der Mechanik keine Möglichkeit, eine absolute Geschwindigkeit gegenüber dem leeren Raum irgendwie dingfest zu machen.

Ein gutes Beispiel für ein Inertialsystems ist ein Raumschiff, das ohne jeden Antrieb und ohne jede Eigenrotation weit entfernt von allen Sternen und Planeten durch den leeren Weltraum treibt. Falls dieses Raumschiff keine Fenster besitzt, so kann man durch irgendwelche mechanischen Experimente innerhalb des Raumschiffs nicht feststellen, ob es sich gleichmäßig bewegt oder nicht. Nur durch einen Blick aus dem Fenster lässt sich eine Geschwindigkeit des Raumschiffs relativ zu den Sternen des Weltalls ermitteln. Hier macht es also keinen Sinn, von einem absolut ruhenden Raum zu sprechen, gegenüber dem sich das Raumschiff bewegt.

Eine Beschleunigung lässt sich dagegen sehr wohl auch ohne einen Blick aus dem Fenster feststellen, denn sie würde einen Astronauten gegen eine der Raumschiffwände drücken – genau dies war ja Newtons Argument für einen absoluten Raum gewesen.

Die Situation ist also nicht ganz eindeutig: Geschwindigkeiten lassen sich nicht absolut messen, Beschleunigungen dagegen schon. Statt vom absoluten Raum muss man daher besser von Inertialsystemen als Maßstab für Bewegungen reden. Alle gleichförmig gegeneinander bewegten Inertialsysteme sind dabei physikalisch vollkommen gleichwertig – es gibt kein absolut ruhendes Inertialsystem – während beschleunigte Bezugssysteme sich je nach Beschleunigung eindeutig physikalisch voneinander unterscheiden. Inertialsysteme ersetzen in diesem Sinn die Idee von einem absoluten Raum, denn sie liefern den Referenzmaßstab für Beschleunigungen, indem sie selber unbeschleunigte Bezugssysteme repräsentieren.

Man muss also sehr vorsichtig sein, wenn man das Relativitätsprinzip für selbstverständlich hält – frei nach dem Motto: "Klar gibt es keine absolute Bewegung, denn man braucht doch immer ein Bezugsobjekt, gegenüber dem man die Bewegung angibt, und absoluter Raum als Bezugsobjekt ist eine reine Illusion." Bei Beschleunigungen gilt diese scheinbar so naheliegende Ansicht offenbar nicht so selbstverständlich.

Der Raum in der speziellen Relativitätstheorie

Wie sieht die Angelegenheit aus, wenn wir neben der Mechanik andere physikalischen Phänomene hinzunehmen, beispielsweise elektromagnetische Phänomene? Kann man beispielsweise anhand der Ausbreitung von Lichtstrahlen innerhalb des Raumschiffs erkennen, ob sich dieses bewegt? Da Licht immer dieselbe Geschwindigkeit von knapp 300000 km/s besitzt, müsste man mit einem Raumschiff doch einem Lichtstrahl hinterherfliegen können, sodass dieser Lichtstrahl vom Raumschiff aus gesehen langsamer sein müsste und man daraus die Eigengeschwindigkeit des Raumschiffs ermitteln könnte.

Aus dem letzten Kapitel wissen wir bereits, dass das genau nicht der Fall ist! Auch vom Raumschiff aus gesehen hat der Lichtstrahl eine Geschwindigkeit von knapp 300000 km/s, egal wie schnell dieses dem Lichtstrahl hinterherfliegt. Das Relativitätsprinzip für Inertialsysteme gilt also nicht nur für die Mechanik, sondern auch für Licht und – wie man nach und nach feststellen musste – für jedes physikalische Phänomen. Außerdem ist damit auch klar, dass man einen Lichtstrahl nicht überholen kann – nichts ist schneller als Licht. Albert Einstein hat diese Erkenntnisse im Jahr 1905 zum Grundprinzip seiner speziellen Relativitätstheorie gemacht:

• Alle Inertialsysteme (gleichförmig bewegte oder ruhende Bezugssysteme) sind physikalisch gleichwertig, d.h. in ihnen gelten dieselben physikalischen Gesetze.

• Die Lichtgeschwindigkeit bildet in jedem Inertialsystem die obere Grenze für die Ausbreitungsgeschwindigkeit physikalischer Wirkungen. Dabei ist sie in jedem Inertialsystem gleich groß.

Für die Zeit haben diese beiden Prinzipien gravierende Auswirkungen, wie wir bereits im letzten Kapitel gesehen haben: Eine Uhr läuft umso langsamer, je schneller sie sich gegenüber uns bewegt. Könnte sie gar mit Lichtgeschwindigkeit fliegen, so würde sie sogar stehenbleiben. Wir haben dies als Zeitdilatation bezeichnet.

Eine absolute Zeit gibt es also gar nicht. Wie aber sieht es mit dem Raum aus?

Die Zeitdilatation führt ganz automatisch dazu, dass es auch einen absoluten Raum nicht geben kann. Um das zu verstehen, schauen wir uns noch einmal das Beispiel der Myonen aus dem letzten Kapitel an, die von der kosmischen Strahlung in der oberen Atmosphäre erzeugt werden: Ein ruhendes Myon würde so schnell zerfallen, dass es den Erdboden praktisch nicht erreichen kann. Dennoch messen wir am Erdboden ankommende Myonen! Das liegt daran, dass sich die Lebensdauer der Myonen aufgrund ihrer großen Geschwindigkeit stark verlängert. Die innere Uhr der schnellen Myonen tickt aufgrund der Zeitdilatation langsamer.

Nun könnten wir dieselbe Situation aber auch aus der Sicht des Myons betrachten, wobei wir vereinfacht annehmen wollen, dass sich das Myon mit gleichförmiger Geschwindigkeit in Richtung Erdboden bewegt, sodass es physikalisch egal sein muss, ob wir die Situation vom Erdboden aus oder aus Sicht des Myons betrachten – beide Inertialsysteme müssen ja gleichwertig sein.

Aus Sicht des Myons bewegt sich der Erdboden sehr schnell auf das Myon zu. Da es selbst aus seiner Sicht ruht, zerfällt es sehr viel schneller als vom Erdboden aus gesehen. Wie aber kann es dann noch den Erdboden erreichen?

Die Lösung lautet: Die Entfernung zwischen Myon und Erdboden ist aus Sicht des Myons kürzer als vom Erdboden aus gesehen! Man nennt dies auch die relativistische Längenkontraktion.

Ganz allgemein wird ein Längenmaßstab in Flugrichtung umso kürzer, je schneller man ihn bewegt. Man muss sich hier davor hüten, von einem scheinbaren Effekt zu sprechen. Wie die Zeitdilatation ist auch die Längenkontraktion ein ganz reales Phänomen mit ganz realen Auswirkungen. Hier ein Beispiel:

Schauen wir uns einen ruhenden sehr langen elektrisch neutralen Draht an, in dem ein elektrischer Strom fließt, d.h. es bewegen sich darin Elektronen mit der Geschwindigkeit v nach rechts. Zugleich befindet sich außerhalb des Drahtes in gewissem Abstand ein einzelnes Elektron, das sich mit derselben Geschwindigkeit v synchron mit den Elektronen im Draht nach rechts bewegt. Der elektrische Strom im ruhenden Draht erzeugt nun ein ringförmiges Magnetfeld um den Draht, sodass auf das bewegte Elektron außerhalb des Drahtes eine Lorentzkraft wirkt, die das Elektron in Richtung Draht zieht.

Wie sieht dieselbe Situation aus, wenn man sich synchron mit den Elektronen im und außerhalb des Drahtes mitbewegt, so dass sowohl das einzelne Elektron außerhalb des Drahtes als auch die Elektronen im Draht ruhend erscheinen? Nach Einstein muss auch die Physik in diesem Bezugssystem von denselben Naturgesetzen regiert werden wie die Physik im Bezugssystem mit ruhendem Draht. Da sich das Einzel-Elektron außerhalb des Drahtes nun nicht mehr bewegt, nimmt es von einem Magnetfeld keine Notiz mehr, d.h. die Lorentzkraft ist Null. Dennoch sollte es in Richtung Draht gezogen werden, denn es handelt sich ja um dieselbe Situation wie vorher, nur aus einem anderen Bezugssystem heraus betrachtet. Was also zieht das Elektron nun zum Draht hin?

Es stellt sich heraus, dass der Draht in diesem neuen Bezugssystem nicht mehr elektrisch neutral ist, sondern positiv elektrisch geladen, d.h. im neuen Bezugssystem übernimmt ein elektrisches Feld die Funktion, die zuvor ein Magnetfeld ausgeübt hat. Der Grund für die elektrische Ladung des Drahtes im neuen Bezugssystem ist die relativistische Längenkontraktion:

Nehmen wir vereinfacht an, dass im Bezugssystem mit ruhendem Draht die nach rechts bewegten Elektronen und die ruhenden Protonen dieselben Abstände voneinander haben, sodass der Draht elektrisch neutral ist. Im anderen Bezugssystem, in dem die nach rechts fliegenden Elektronen ruhen, verkürzt sich der Abstand zwischen den sich nun nach links bewegenden Protonen, während die nun ruhenden Elektronen einen größeren Abstand als zuvor voneinander haben. Die Dichte der Protonen wird also größer, die der Elektronen geringer, sodass der Draht positiv geladen ist und das Elektron anzieht.

Wir sehen also, wie die relativistische Längenkontraktion dafür sorgt, dass in beiden Bezugssystemen derselbe Effekt eintritt: das Elektron wird vom Draht angezogen. In diesem Sinne kann man sogar sagen, dass Magnetfelder letztlich eine Folge der relativistischen Längenkontraktion sind. Auch bei den eigentlich recht kleinen Elektronen-Geschwindigkeiten, wie sie in realen stromführenden Drähten auftreten, wirkt sich dieser relativistische Effekt bereits aus, denn die elektromagnetische Kraft ist sehr viel stärker als beispielsweise die Gravitationskraft.

Anschaulich erscheint es zunächst merkwürdig, dass sich die positive Protonendichte und die relativ dazu bewegte negative Elektronendichte im Draht beim Wechsel des Bezugssystems unterschiedlich verhalten. Elektronen und Protonen müssten sich doch in beiden Bezugssystemen jeweils an denselben Stellen im Draht befinden. Doch Vorsicht: die Elektronen bewegen sich gegenüber dem Draht. Man muss also in jedem Bezugssystem genau angeben, wann sie sich wo befinden. Und dieses WANN macht den Unterschied, denn beim Wechsel des Bezugssystems sind zuvor gleichzeitige Ereignisse nicht mehr gleichzeitig (mit Ereignis bezeichnet man allgemein einen Punkt in der Raumzeit, also etwas, das durch die Angabe von Zeit und Ort gekennzeichnet ist). Die gleichzeitigen Orte der Elektronen und Protonen gehören in beiden Bezugssystemen nicht zu denselben Ereignissen. Nur wenn man die Veränderungen in Raum und Zeit beide konsistent berücksichtigt, kann man die beschriebene Veränderung der Ladungsdichten verstehen.

Es gibt also offenbar eine Relativität der Gleichzeitigkeit. Was verbirgt sich dahinter?

Stellen wir uns dazu zwei Raumschiffe vor, die sich für einen außenstehenden Beobachter sehr schnell mit konstantem Abstand nach rechts bewegen. Ein Astronaut in einem der Raumschiffe sieht dagegen einfach nur zwei ruhende Raumschiffe, deren Abstand sich nicht ändert. Den Abstand zwischen den Raumschiffen kann er mit einem Lichtblitz ermitteln, den er zu seinem Nachbarraumschiff aussendet, wo er wieder zurückgespiegelt wird. Wenn dieser zurückgespiegelte Lichtblitz nach 2 Sekunden wieder beim Astronauten ankommt, so weiß dieser, dass die beiden Raumschiffe eine Lichtsekunde voneinander entfernt sind, also knapp 300000 Kilometer. Die Lichtgeschwindigkeit hat ja in jedem Inertialsystem denselben Wert von knapp 300000 km pro Sekunde.

Mit diesem Lichtblitz können beide Raumschiffe ihre Uhren synchronisieren: Der Astronaut setzt seine Uhr eine Sekunde nach Abschicken des Lichtblitzes auf Null, also genau zwischen dem Abschicken und dem Wiedereintreffen des Lichtblitzes, während das andere Raumschiff seine Uhr beim Eintreffen und Zurückspiegeln des Lichtblitzes auf Null setzt. Die beiden Ereignisse Uhr auf Null setzen in Raumschiff A und Uhr auf Null setzen in Raumschiff B finden aus Sicht der Raumschiffe gleichzeitig statt. Beide Uhren laufen ab diesem Moment synchron, was die Raumschiffe jederzeit durch den Austausch von Lichtsignalen überprüfen können.

Wie sieht dieselbe Situation für den außenstehenden Beobachter aus, der die beiden Raumschiffe mit hoher Geschwindigkeit in der Ferne vorbeiziehen sieht? Auch für diesen Beobachter breitet sich Licht in allen Richtungen mit 300000 km/s aus! Nehmen wir an, das hintere Raumschiff sendet den Lichtblitz aus, der dann vom vorderen Raumschiff zurückgespiegelt wird und wieder beim hinteren Raumschiff eintrifft. Genau zwischen dem Aussenden und dem Wiedereintreffen stellt der Astronaut im hinteren Raumschiff aus seiner Sicht seine Uhr auf Null. Im vorderen Raumschiff wird die Uhr aber erst später auf Null gestellt, denn dieses Raumschiff fliegt ja zunächst dem Lichtblitz davon und spiegelt ihn daher erst später zurück, worauf dieser dem vorderen Raumschiff entgegenfliegt und dort eintrifft. Auf dem Hinweg zum vorderen Raumschiff braucht der Lichtblitz also mehr Zeit als auf dem Rückweg zum hinteren Raumschiff, sodass das Zurückspiegeln nicht genau zwischen dem Aussenden und Wiedereintreffen des Lichtblitzes stattfindet, sondern später. Die beiden Ereignisse Uhr auf Null setzen in Raumschiff A und Uhr auf Null setzen in Raumschiff B finden aus Sicht des außenstehenden Beobachters also nicht gleichzeitig statt.

Die Relativität der Gleichzeitigkeit ist eng verknüpft mit der Zeitdilatation und der Längenkontraktion. Um einen Abstand zu bestimmen, braucht man nämlich zwei gleichzeitige Ereignisse. Bei einem ruhenden Längenmaßstab ist das kein Problem, denn sein vorderes und hinteres Ende sind ja immer an derselben Stelle. Bewegt sich der Maßstab jedoch, so braucht man die beiden Orte, die sein vorderes und hinteres Ende zu einer bestimmten Zeit gleichzeitig einnehmen. Die beiden Ereignisse, deren räumlichen Abstand man misst, sind also die gleichzeitigen Positionen der beiden Enden zu einer bestimmten Zeit. Je nach Geschwindigkeit des Maßstabes verändert sich aber die Definition der Ereignisse, die man als gleichzeitig ansieht, relativ zu dem, was man aus Sicht des Maßstabs als gleichzeitig ansieht. Daher sind es unterschiedliche Ereignisse, die man je nach Bezugssystem heranzieht, um deren räumlichen Abstand zu messen. Kein Wunder also, dass nicht immer derselbe Abstand herauskommt!

Genau das kann man auch gut in der obigen Abbildung erkennen: Während die beiden ruhenden Raumschiffe im Bild links 10 Maßeinheiten voneinander entfernt sind, beträgt ihr Abstand im Bild rechts nur noch knapp 8,7 Längeneinheiten. Dabei vergleicht man aber im linken und rechten Bild den räumlichen Abstand unterschiedlicher Ereignisse miteinander!

Die Abbildung zeigt: Die beiden Beobachter teilen mit ihren Inertialsystemen die Raumzeit in unterschiedlicher Weise in verschiedene Gleichzeitigkeits-Scheiben auf – in der Abbildung durch waagerechte Linien gekennzeichnet. Wenn wir den Raum, der in einem bestimmten Moment existiert, mit so einer Gleichzeitigkeits-Scheibe der Raumzeit identifizieren, so hängt es vom Beobachter und seiner Eigenbewegung ab, welche Ereignisse der Raumzeit zu diesem Raum zusammengefasst werden. Raum und Zeit sind so eng miteinander verwoben, dass es kaum noch Sinn macht, die voneinander zu trennen. Hermann Minkowski hat diesen engen Zusammenhang als Erster in seiner gesamten Tiefe erkannt und die mathematischen Grundlagen zur Beschreibung der Raumzeit gelegt. In einer berühmten Ansprache Raum und Zeit auf der Versammlung der Deutschen Gesellschaft der Naturforscher und Ärzte (Jahresberichte der Deutschen Mathematiker- Vereinigung, Leipzig, 1908) drückte er diese bahnbrechende Erkenntnis so aus:

"Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren."

Wie sieht die mathematische Beschreibung der Raumzeit aus, die Minkowski formuliert hatte (wer möchte, kann diesen Abschnitt gerne überspringen)? Wir kennen sie weitgehend schon aus dem letzten Kapitel über die Zeit, als wir und mit der Eigenzeit beschäftigt hatten. Die Grundfrage dabei ist: Wenn sich beim Wechsel von einem Inertialsystem zu einem anderen Inertialsystem die Raum- und Zeitkoordinaten der Ereignisse in der Raumzeit ändern können, sodass sich sogar die Einschätzung von Raum- und Zeitintervallen dabei verändern kann, was bleibt dann eigentlich noch bestehen?

Orientierung bildet die Konstanz der Lichtgeschwindigkeit \(c\), die für jeden Beobachter dieselbe sein muss. Daraus kann man letztlich ablesen, dass für zwei Ereignisse mit Zeitpunkten \(t_1\) und \(t_2\) an den Orten \( \boldsymbol{x}_1 \) und \( \boldsymbol{x}_2 \) der folgende Ausdruck sich nicht ändert, wenn wir die Zeiten und Orte der beiden Ereignisse in verschiedenen Inertialsystemen ermitteln: \begin{equation} (c \, \Delta t)^2 - (\Delta \boldsymbol{x})^2 = \mathrm{konstant} \end{equation} Dabei ist \( \Delta t = t_2 - t_1 \) das entsprechende Zeitintervall zwischen den beiden Zeitpunkten, und \( \Delta \boldsymbol{x} = \boldsymbol{x}_2 - \boldsymbol{x}_1 \) ist der räumliche Verbindungsvektor zwischen den beiden Ortspunkten. Sowohl \( \Delta t \) als auch \( \Delta \boldsymbol{x} \) können in verschiedenen Inertialsystemen unterschiedliche Werte aufweisen, aber die obige Differenz der Quadrate – die man als Minkowskimetrik bezeichnet – ist unabhängig vom Bezugssystem.

Was hat diese Differenz nun mit der Konstanz der Lichtgeschwindigkeit c zu tun? Ganz einfach: Wenn das erste Ereignis die Erzeugung und das zweite Ereignis das Eintreffen eines Lichtblitzes kennzeichnet, so ist der obige Ausdruck in jedem Bezugssystem gleich Null, sodass für die entsprechenden Raumzeitintervalle immer \( | c \, \Delta t | = | \Delta \boldsymbol{x} | \) gilt. Der Lichtblitz ist also in jedem Bezugssystem gleich schnell. Zwei solche Ereignisse bezeichnet man auch als lichtartig zueinander.

Es gibt natürlich noch andere Möglichkeiten für die beiden Ereignisse. So kann beispielsweise ein antriebslos dahingleitendes Raumschiff sich zur Zeit \(t_1\) am Ort \( \boldsymbol{x}_1 \) und zur Zeit \(t_2\) am Ort \( \boldsymbol{x}_2 \) befinden. Die beiden Ereignisse liegen dann zeitartig zueinander, denn man kann sich in das Bezugssystems des dahingleitenden Raumschiffs begeben, sodass das Raumschiff als ruhend erscheint und \( \Delta \boldsymbol{x} = 0 \) wird. Der obige Term ist dann positiv und gibt das Quadrat der Eigenzeit \( \Delta \tau \) (mal \(c\) ) an, die auf einer Uhr im Raumschiff auf dem Weg zwischen den beiden Ereignissen vergeht – das kennen wir bereits aus dem letzten Kapitel.

Bleibt die dritte Möglichkeit, bei welcher der obige Ausdruck negativ ist. In diesem Fall sind die Orte der beiden Ereignisse so weit voneinander entfernt, dass ein Lichtstrahl die zwischen ihnen liegende Strecke \( | \Delta \boldsymbol{x} | \) in der zur Verfügung stehenden Zeit \( \Delta t \) nicht überwinden kann. Da keine physikalische Wirkung sich schneller als mit Lichtgeschwindigkeit ausbreiten kann, können die beiden Ereignisse nicht in kausalem Zusammenhang zueinander stehen. Es hängt nun vom Bezugssystem ab, welches der beiden Ereignisse das frühere und welches das spätere Ereignis ist. Ihre zeitliche Reihenfolge ist also nicht universell festgelegt, sondern kann je nach Beobachter unterschiedlich sein. Man kann sogar immer ein Bezugssystem finden, in dem \( \Delta t = 0 \) ist, sodass beide Ereignisse in diesem Bezugssystem gleichzeitig stattfinden. Zwei solche Ereignisse bezeichnet man daher als raumartig zueinander.

Sind die Naturgesetze spiegelsymmetrisch?

Mit dem Relativitätsprinzip ist uns etwas begegnet, das man in der Physik als Symmetrieprinzip bezeichnet: Es ist egal, aus welchem Inertialsystem heraus man einen physikalischen Prozess betrachtet, denn die physikalischen Gesetze sind in allen Inertialsystemen genau gleich. Aus jedem Inertialsystem heraus sieht man ein nach denselben Gesetzen mögliches physikalisches Phänomen.

Ein ähnliches Symmetrieprinzip kennen wir bereits von der Zeit: Die physikalischen Gesetze sind dieselben, wenn man die Zeit rückwärts laufen lässt – von Ausnahmen bei bestimmten seltenen Teilchenzerfällen einmal abgesehen. Erst der extrem unwahrscheinliche Anfangszustand unseres Universums lässt einen Zeitpfeil entstehen.

Eine Zeitspiegelung ändert also die Naturgesetze normalerweise nicht. Gilt dasselbe auch für eine Raumspiegelung? Hat jedes physikalische Experiment im leeren Weltraum dasselbe Ergebnis, wenn man es raumgespiegelt betrachtet, also vorne und hinten, oben und unten sowie rechts und links vertauscht? Oder erkennt man einen Unterschied?

Man kann die Fragestellung etwas vereinfachen, da es genügt, beispielsweise nur rechts und links zu vertauschen, da die anderen beiden Vertauschungen zusammen nur eine 180-Grad-Drehung ergeben. Da alle Experimente zeigen, dass die Naturgesetze drehsymmetrisch sind, sollte eine 180-Grad-Drehung keine Rolle spielen. Wir können also einfach fragen: Kann man bei einem Experiment erkennen, ob man es in einem Spiegel betrachtet oder nicht? Das ist gemeint, wenn wir danach fragen, ob die Naturgesetze spiegelsymmetrisch sind.

Was würden Sie als Antwort erwarten? Wieder ist es gar nicht einfach, sich intuitiv eine Meinung dazu zu bilden. Bei der Gravitation, der elektromagnetischen Kraft und der starken Kernkraft sind alle damit zusammenhängenden Phänomene vollkommen spiegelsymmetrisch, d.h. betrachtet man ein solches Phänomen in einem Spiegel, so sieht man wieder einen physikalisch möglichen Prozess. Jeder hatte daher auch bei der vierten fundamentalen Wechselwirkung – der sogenannten schwachen Wechselwirkung – erwartet, dass diese ebenfalls spiegelsymmetrisch sein müsse. Mitte des zwanzigsten Jahrhunderts war es schon fast ein Dogma, dass die Naturgesetze spiegelsymmetrisch sind.

Die schwache Wechselwirkung ist uns weit weniger geläufig als die drei anderen Wechselwirkungen. Sie hat eine extrem kurze Reichweite, sodass es keine spürbaren Kraftfelder zu dieser Wechselwirkung gibt. Daher spielt die schwache Wechselwirkung in unserer Umwelt kaum eine Rolle. Dennoch ist sie extrem wichtig, denn sie kann in weit größerem Maße als die anderen drei Wechselwirkungen verschiedene Teilchen ineinander umwandeln, sodass sie für die meisten Teilchenzerfälle und Teilchenumwandlungen verantwortlich ist. Ohne die schwache Wechselwirkung würde unsere Sonne nicht leuchten, denn bei der Kernfusion in ihrem Inneren müssen sich Protonen in Neutronen umwandeln, sodass diese dann mit weiteren Protonen zu Heliumkernen fusionieren können.

Im Jahr 1956 gab es nun eine Überraschung: Man untersuchte im Detail, ob es bei Teilchenzerfällen aufgrund der schwachen Wechselwirkung eine Rolle spielt, ob man das Experiment spiegelverkehrt aufbaut oder nicht. Dabei fand man heraus, dass die Winkelverteilung der Zerfallsprodukte sich bei einer Raumspiegelung ändert. Die Naturgesetze sind nicht spiegelsymmetrisch – zumindest was die schwache Wechselwirkung betrifft.

Besonders deutlich wird diese Verletzung der Spiegelsymmetrie bei einem Teilchen, das weder durch die elektromagnetische noch durch die starke Wechselwirkung beeinflusst wird – die Gravitation spielt wegen ihrer geringen Stärke bei einzelnen Teilchen sowieso kaum eine Rolle. Dieses besondere Teilchen ist das Neutrino. Es kann nur durch die schwache Wechselwirkung beeinflusst, erzeugt und vernichtet werden, sodass es auch große Materieansammlungen wie unsere Erde nahezu ungehindert durchquert. Genau das geschieht in jeder Sekunde Milliardenfach, denn bei der erwähnten Umwandlung von Protonen zu Neutronen im Sonnenzentrum entstehen große Mengen dieser geisterhaften Teilchen. Auch viele andere Prozesse im Universum erzeugen Neutrinos, sodass Neutrinos nach Photonen tatsächlich die häufigsten Teilchen im Universum sind!

Da Neutrinos nahezu masselos sind, bewegen sie sich fast mit Lichtgeschwindigkeit. Dabei besitzt ein Neutrino eine quantenmechanische Eigenrotation (einen Spin) um sein Flugachse, wobei es in Flugrichtung betrachtet immer gegen den Uhrzeigersinn rotiert – also links herum. Es gibt demnach nur links herum rotierende Neutrinos! Würde man ein solches Neutrino in einem Spiegel betrachten, so würde es rechts herum rotieren – solche Neutrinos kann aber die schwache Wechselwirkung nicht erzeugen. Die Spiegelsymmetrie ist verletzt!

Wenn wir jedoch die Situation nicht nur im Spiegel betrachten, sondern zusätzlich jedes Teilchen durch sein Antiteilchen ersetzen, so haben wir wieder ein physikalisch mögliches Geschehen vor uns, denn Antineutrinos rotieren genau entgegengesetzt zu Neutrinos – also rechts herum. Man könnte also vermuten, dass die Naturgesetze wieder unverändert gelten, wenn wir nicht nur den Raum spiegeln, sondern zusätzlich Teilchen durch Antiteilchen ersetzen und umgekehrt. So etwas bezeichnet man auch als CP-Invarianz, wobei C für charge conjugation – also Teilchen-Antiteilchen-Austausch – und P für parity – also Raumspiegelung – steht.

Bei den meisten Zerfällen gilt die CP-Invarianz tatsächlich. Im Jahr 1964 fand man aber winzige Abweichungen von dieser Invarianz bei bestimmten Teilchenzerfällen. Erst wenn man zusätzlich noch die Zeit spiegelt (also im Prinzip das Experiment zeitlich rückwärts betrachtet), dann hat man wieder eine Invarianz vor sich, die bis heute jeden Test bestanden hat: die CPT-Invarianz, wobei T für time reversal steht. Diese Invarianz ist uns bereits kurz im letzten Kapitel begegnet.

Wie wir sehen, entfernt sich die physikalische Natur des Raumes immer weiter von dem anschaulichen Bild, das Newton noch vorschwebte. Der Raum ist einerseits eng mit der Zeit verwoben und erlaubt keine Bestimmung absoluter Geschwindigkeiten, und andererseits sind die in ihm geltenden Naturgesetze auch nicht immer spiegelsymmetrisch. Er könnte aber immer noch zusammen mit der Zeit eine Art unbeteiligte Bühne für die in ihm ablaufenden Prozesse darstellen, ohne selbst von diesen Prozessen verändert zu werden. Die Raumzeit wäre dieselbe, ob sich darin nun ein Stern befindet oder nicht. Ist diese Vorstellung korrekt, oder erleben wir erneut eine Überaschung?

Gekrümmte Räume

In welcher Weise könnten Raum und Zeit überhaupt davon abhängen, welche Prozesse sich gerade in ihnen abspielen? Inwiefern könnten sich Raum und Zeit dabei überhaupt verändern?

Newton hatte angenommen, dass der Raum euklidisch ist – die Winkelsumme in einem Dreieck beträgt hier immer 180 Grad. Das ändert sich auch in der speziellen Relativitätstheorie nicht. Doch wer sagt eigentlich, dass der Raum tatsächlich euklidisch sein muss?

Tatsächlich gibt es in der Mathematik viele andere Räume, die nicht euklidisch sind. Ein Beispiel für einen solchen Raum ist die Oberfläche einer Kugel: Sie ist zweidimensional und gekrümmt – also nicht-euklidisch. Die Winkelsumme eines Dreiecks auf der Kugeloberfläche ist größer als 180 Grad!

Ganz allgemein spricht man in der Mathematik bei solchen Räumen von sogenannten Mannigfaltigkeiten. Lokal – also im Kleinen – sieht eine n-dimensionale Mannigfaltigkeit immer aus wie der n-dimensionale euklidische Raum. Entsprechend erscheint uns unsere Erdoberfläche lokal wie eine zweidimensionale Ebene. Erst bei größeren Entfernungen macht sich die Erdkrümmung bemerkbar.

Wichtig ist, dass ein Raum auch eine Krümmung aufweisen kann, ohne dass er in einem höherdimensionalen Raum eingebettet sein muss, wie das beispielsweise bei der Kugeloberfläche der Fall ist. Man kann auch ohne eine Blick von außen in dem Raum selbst feststellen, ob er gekrümmt ist, beispielsweise indem man die Winkelsumme von möglichst großen Dreiecken misst.

Wie kann man sich einen gekrümmten Raum veranschaulichen, ohne ihn von außen zu betrachten? Eine einfache Möglichkeit ist die Folgende: Man zerschneidet den Raum in viele möglichst kleine Stücke und gibt an, wie diese Stücke miteinander zusammenhängen, sodass man bei einer Reise durch den Raum immer weiß, in welches Stück man wo eintritt, wenn man ein anderes Stück verlässt.

Schauen wir uns das konkret bei der Kugeloberfläche an: Wie beim Schälen einer Orange zerschneiden wir diese Oberfläche entlang der Längengrade vom Nordpol zum Südpol in schmale Streifen. Dann nehmen wir die Streifen vom Südpol ausgehend auseinander und drücken sie platt auf eine Ebene, sodass der Nordpol in der Mitte liegt. Dieses Plattdrücken geht umso besser, je schmaler wie die Streifen schneiden. Die Streifen ragen nun sternförmig nach allen Seiten auseinander, wobei sie nach außen hin zunächst breiter und dann wieder schmaler werden. Dabei entspricht die Schnittkante eines Streifens der Schnittkante des Nachbarstreifens, denn beide Kanten gehören zu denselben Punkten eines Längengrades auf der Kugeloberfläche. Die außenliegenden Spitzen entsprechen sogar nur einem einzigen Punkt der Kugeloberfläche: dem Südpol.

   

Man kann sich nun jede Bewegung auf der Kugeloberfläche durch eine entsprechende Bewegung innerhalb der dünnen Streifen veranschaulichen, wobei man an den Schnittkanten von einem Streifen zu dessen Nachbarstreifen hüpft. Wenn man sich beispielsweise auf der Kugel geradeaus bewegt, so bewegt man sich auf jedem einzelnen Streifen ebenfalls geradeaus. An den Kanten tritt man in den nächsten Streifen mit demselben Winkel relativ zur Kante ein, mit dem man den vorherigen Streifen verlassen hat, denn man muss sich die Streifen ja entlang dieser Kante zusammengeklebt vorstellen. Verfolgt man diese Bewegung auf den Streifen sorgfältig weiter, so stellt man schließlich fest, dass sie einen wieder an den Ausgangspunkt zurückführt. Man hat die Kugel dabei entlang eines Großkreises einmal umrundet.

Mit diesem Trick ist es auch beispielsweise möglich, sich das dreidimensionale Analogon der Kugeloberfläche zu veranschaulichen: die 3-Sphäre (die Kugeloberfläche heißt entsprechend auch 2-Sphäre, da sie eine 2-dimensionale Fläche ist – siehe auch Die 3-Sphäre und die Poincaré-Vermutung). Die 3-Sphäre lässt sich ganz ähnlich wie die Kugeloberfläche zerschneiden, nur dass diesmal keine zweidimensionalen Streifen dabei entstehen, sondern dreidimensionale längliche Stücke, die man sich wie gerade Bohnen oder Schupfnudeln vorstellen kann, allerdings nicht mit rundem, sondern mit annähernd viereckigem bzw. trapezförmigem Querschnitt – das Zerschneiden erzeugt ja Seitenflächen bei den einzelnen Teilstücken der 3-Sphäre. Die Stücke haben dabei zwei Spitzen, die dem Nord- und Südpol entsprechen, und werden zur Mitte hin dicker. Wir können die Stücke am Nordpol miteinander verbunden lassen, sodass sie wie die Stacheln eines Seeigels nach allen Seiten auseinanderstehen. Dabei liegen die Stacheln ganz innen noch dicht an dicht, aber die Lücken zwischen ihnen werden immer größer, je weiter man nach außen kommt. Die Spitzen ganz außen entsprechen dann dem Südpol.

Auch in dieser zerschnittenen 3-Sphäre kann man analog zur 2-Sphäre geradeaus laufen, wobei man an den Schnittflächen so zum Nachbarstück springen muss, als wären sie dort zusammengeklebt. Dabei würde man nie an eine Grenze stoßen, sondern schließlich an seinen Ausgangspunkt zurückkehren. Die 3-Sphäre ist also wie die Kugeloberfläche endlich, obwohl sie keine Begrenzung besitzt.

Linien, die durch Geradeaus-Laufen in einem gekrümmten Raum entstehen, nennt man auch Geodäten. Mit drei Geodäten lassen sich größere Dreiecke in der 3-Sphäre konstruieren und deren Winkelsumme bestimmen. Es wundert uns nicht, dass diese Winkelsumme größer als 180 Grad ist, und zwar umso mehr, je größer das Dreieck ist.

Wenn wir nun herausfinden wollen, ob unser eigener Raum euklidisch ist, dann können wir dies also beispielsweise durch die Vermessung von Dreiecken feststellen. Einer der ersten, der die Möglichkeit nicht-euklidischer Räume ernst nahmen und sie auch mathematisch intensiv untersuchte, war der deutsche Mathematiker Carl-Friedrich Gauß. Bei der Hannoverschen Landesvermessung hatte er beispielsweise das Dreieck, das vom Brocken im Harz, dem Inselsberg im Thüringer Wald und dem Hohen Hagen bei Dransfeld gebildet wird, intensiv vermessen. Der Legende nach hat er dabei auch nach Abweichungen in der Winkelsumme von 180 Grad gesucht, aber keine solche Abweichung finden können. Innerhalb der Messgenauigkeit ist der uns umgebende Raum also offenbar tatsächlich euklidisch.

Die Gravitation krümmt Raum und Zeit

Auch wenn die ersten Messungen von Carl-Friedrich Gauß nahelegen, dass unser Raum euklidisch ist, so wissen wir aus dem letzten Kapitel, dass dies nicht der Fall ist: Raum und Zeit sind nach Albert Einsteins Allgemeiner Relativitätstheorie in einem Gravitationsfeld normalerweise gekrümmt! Allerdings ist diese Krümmung durch das Gravitationsfeld der Erde so gering, dass Gauß sie im Rahmen seiner Messgenauigkeit nicht entdecken konnte.

Nachdem Albert Einstein im Jahr 1915 seine Allgemeine Relativitätstheorie veröffentlicht hatte, wartete natürlich die ganze Welt auf einen Nachweis der von ihm vorhergesagten Krümmung von Raum und Zeit. Dies gelang Arthur Stanley Eddington und Frank Dyson im Jahr 1919. Sie nutzen dabei eine totale Sonnenfinsternis, um die Position eines Sterns zu bestimmen, dessen Licht auf dem Weg zu uns sehr nahe an der Sonne vorbeikam. Die starke Gravitation der Sonne sollte dabei die umgebende Raumzeit so deutlich krümmen, dass das Sternenlicht leicht abgelenkt werden müsste und wir den Stern daher an einer etwas verschobenen Position sehen würden, als dies ohne die Raumkrümmung der Fall wäre. Tatsächlich fand man genau die vorhergesagte Abweichung in der Sternenposition, und Albert Einstein wurde über Nacht zu einem berühmten Mann.

Heute ist die Ablenkung von Licht durch die Gravitation zu einem häufig beobachteten Phänomen geworden: Das Licht sehr ferner Galaxien wird oft durch andere Materieansammlungen auf seinem Weg zu uns abgelenkt, wobei sich die Raumkrümmung teilweise wie eine Linse auswirkt – man spricht deshalb von Gravitationslinsen. Manchmal kann das Licht von extrem weit entfernten Galaxien dabei so verstärkt werden, dass wir sie gerade noch beobachten können – ohne Gravitationslinsen wären unsere Teleskope zu schwach dafür gewesen.

In der Speziellen Relativitätstheorie stellen Raum und Zeit noch eine unbeteiligte Bühne für die in ihnen ablaufenden Prozesse dar, ohne dass sie selbst von diesen Prozessen verändert werden. Die Raumzeit ist dieselbe, ob sich darin nun ein Stern befindet oder nicht. Das ändert sich in Einsteins Allgemeiner Relativitätstheorie grundlegend: Materie, Energie und sogar Druck erzeugen eine Krümmung in Raum und Zeit und bewirken so die Gravitation darin. Raum und Zeit werden nun selbst zu physikalischen Akteuren! Wenn große Massen dabei starken Beschleunigungen unterliegen – beispielsweise wenn sich Neutronensterne oder Schwarze Löcher gegenseitig eng umkreisen oder gar miteinander verschmelzen – dann geraten Raum und Zeit sogar in regelrechte Schwingungen, die sich wellenförmig ausbreiten. Indirekt hat man solche Gravitationswellen bereits nachweisen können, denn die einander umkreisenden Neutronensterne oder Schwarzen Löcher verlieren genau in dem Maße Energie, wie sie durch die Abstrahlung von Gravitationswellen verloren gehen muss. Der direkte Nachweis von Gravitationswellen steht allerdings noch aus, denn Gravitationswellen sind für die heutigen Detektoren im Allgemeinen zu schwach. In naher Zukunft könnte sich die Genauigkeit aber soweit steigern lassen, dass der direkte Nachweis endlich gelingt.

Einstein konnte mit seiner Beschreibung der Gravitation ein Problem lösen, dem Newton noch hilflos gegenüberstand: Wie schafft es die Gravitation eines Körpers, durch den leeren Raum hinweg über große Entfernungen einen anderen Körper zu beeinflussen und aus seiner Bahn abzulenken? Wie kommt diese Fernwirkung zustande, und wie schnell kann sie große Entfernungen zurücklegen? Nach Newtons Gravitationsgesetz müsste sich diese Fernwirkung sogar unendlich schnell ausbreiten, da sich die Position eines Körpers über seine Gravitation unmittelbar auf alle anderen Körper auswirkt – im Widerspruch zu Einsteins Spezieller Relativitätstheorie!

Auch Newton selbst war skeptisch, was diesen Aspekt seines Gravitationsgesetzes betraf. So schrieb er in einem Brief an Richard Bentley von 1692/1693 (Herbert Westren Turnbull, The correspondence of Isaac Newton 1961, Vol. III, S. 253-254, siehe auch Wikipedia: Nahwirkung und Fernwirkung):

"Es ist undenkbar, dass leblose, rohe Materie auf andere [...] Materie wirken sollte, ohne direkten Kontakt und ohne die Vermittlung von etwas anderem, das nicht materiell ist. Dass die Gravitation eine angeborene, inhärente und wesentliche (Eigenschaft) der Materie sein soll, so dass ein Körper auf einen anderen über eine Entfernung durch Vakuum hindurch und ohne die Vermittlung von etwas Sonstigem wirken soll, [...], ist für mich eine so große Absurdität, dass ich glaube, kein Mensch, der eine in philosophischen Dingen geschulte Denkfähigkeit hat, kann sich dem jemals anschließen. Gravitation muss durch einen Vermittler erzeugt werden, welcher gleichmäßig nach bestimmten Gesetzen wirkt. Aber ob dieser Vermittler materiell oder immateriell ist, habe ich der Überlegung meiner Leser überlassen."

Newton suchte also nach einem Vermittler für die Gravitation. Für lange Zeit galt der sogenannte Äther als ein solcher möglicher Vermittler. Dieser Äther war dabei eine hypothetische Substanz, die den Raum vollkommen durchdringen sollte, ohne dass wir sie direkt wahrnehmen können. Auch für die Ausbreitung von elektromagnetischen Kräften und Wellen war ein solcher Äther als vermittelndes Medium im Gespräch. Licht sollte sich dabei als Welle im Äther ausbreiten, ganz so wie Wasserwellen dies an einer Wasseroberfläche tun.

Wenn aber Licht eine Welle im Äther war, dann müsste man Licht einholen und sogar überholen können, wenn man sich nur schnell genug gegenüber dem Äther bewegt. Der Äther würde damit das absolut ruhende Bezugssystem für den leeren Raum liefern. Das Problem war nur, dass man es nie schaffte, auch nur im geringsten Maße einem Lichtstrahl hinterherzulaufen und so eine geringere Lichtgeschwindigkeit zu messen. Licht war immer gleich schnell. Daher verwundert es nicht, dass man die Idee des Äthers schließlich über Bord warf.

In Einsteins Allgemeiner Relativitätstheorie übernehmen Raum und Zeit selbst die Rolle des Vermittlers, indem sie sich unter dem Einfluss von Materie krümmen und so den Lauf anderer Objekte beeinflusst. Dabei bleibt auch sichergestellt, dass sich keine physikalische Wirkung schneller als mit Lichtgeschwindigkeit ausbreitet. Auch Gravitationswellen bewegen sich mit Lichtgeschwindigkeit.

Wie man sich einen gekrümmten dreidimensionalen Raum konkret vorstellen kann, hatten wir oben bereits gesehen: Man zerlegt ihn in kleine Teilstücke und gibt an, wie diese Stücke an den Schnittflächen zusammengehören. In einfachen Fällen mit hoher Symmetrie kann man allerdings noch einfacher vorgehen, indem man uninteressante Raumdimensionen einfach weglässt, sodass man die gekrümmte Restfläche in den dreidimensionalen Raum einbetten kann. Ein solcher Fall liegt beim Gravitationsfeld kugelförmiger Himmelskörper vor, also beim Gravitationsfeld der Erde oder der Sonne, aber auch beim Gravitationsfeld von Neutronensternen und Schwarzer Löcher, sofern diese nicht zu schnell rotieren.

Das Gravitationsfeld dieser Himmelskörper ist kugelsymmetrisch, sodass es genügt, wenn wir uns eine Schnittebene des Raums herausgreifen, die durch den Mittelpunkt des Himmelskörpers geht, beispielsweise die Äquatorebene. Die Raumkrümmung dieser Schnittebene können wir uns nun dadurch veranschaulichen, dass wir sie als gekrümmte zweidimensionale Fläche in den dreidimensionalen Raum einbetten. Die Fläche, die dabei entsteht, sehen wir in der folgenden Abbildung – sie wird als Flamm'sches Paraboloid bezeichnet, da sie aus einer gekippten halben Parabel entsteht, die man um eine Achse jenseits ihrer Spitze rotieren lässt:

Die Fläche ähnelt einem Trichter: Außen wird sie immer flacher – ein Zeichen dafür, dass Gravitation und Raumkrümmung abnehmen, wenn man sich vom Himmelskörper entfernt. Zur Mitte hin, wo sich auch der kugelförmige Himmelskörper befindet, krümmt sich die Fläche dagegen zunehmend nach unten.

Wie muss man nun die gekrümmte Fläche interpretieren? Sie stellt die geometrischen Raumverhältnisse beispielsweise in der Äquatorebene dar, wie sie ein ruhender Beobachter im leeren Raum außerhalb des Himmelskörpers wahrnimmt. Kreise auf dieser Trichterfläche entsprechen dabei gleich großen Kreisen um den Himmelskörper in der Äquatorebene. Den Umfang eines solchen Kreises kann man leicht ausrechnen: er ist gleich zwei mal pi mal dem Radius des Kreises, und dieser Kreisradius ist im Trichterbild einfach der Abstand des Kreises von der senkrechten Symmetrieachse. Aber: dieser Abstand ist nicht identisch mit dem Abstand des Kreises zum Mittelpunkt des Himmelskörpers, denn dafür müssten wir uns entlang der Trichterfläche zur Mitte hin bewegen und die Länge dieser Strecke auf der gekrümmten Fläche abmessen.

Nun hat die Trichterfläche in der Mitte ein Loch, sodass wir uns gar nicht auf der Fläche bis zur Mitte bewegen können! In den meisten Fällen ist das Loch jedoch bedeutungslos: Der Himmelskörper ist normalerweise wesentlich größer als das Loch, und nur außerhalb des Himmelskörpers ist die dargestellte Trichterfläche anwendbar und gibt die Raumkrümmung korrekt wieder. Innerhalb des Himmelskörpers muss die Trichterfläche durch eine andere Fläche nach innen hin fortgesetzt werden, die man sich wie eine Mulde vorstellen kann und die kein Loch mehr aufweist. Das Loch ist damit geschlossen und man kann sich entlang der Fläche bis zur Mitte hin bewegen.

Wir sehen also: Die Raumkrümmung bewirkt, dass Umfang und Radius eines Kreises sich nicht mehr so zueinander verhalten, wie wir das von flachen Räumen her gewöhnt sind – ganz analog zur Winkelsumme eines Dreiecks. Der Abstand zum Mittelpunkt des Himmelskörpers ist größer, als es der Kreisumfang vermuten lässt. Dieser Effekt ist jedoch beispielsweise im Gravitationsfeld der Erde sehr klein, d.h. die Erde ist wesentlich größer als das Loch in der Trichterfläche, das bei der Erde nur einen Durchmesser von rund 2 cm hat. Außerdem spielt für die Gravitation die Krümmung der Zeit eine ganz entscheidende Rolle, wie wir im letzten Kapitel gesehen haben: Die Zeit läuft weiter unten etwas langsamer, und frei fallende Objekte wählen zwischen zwei Raum-Zeit-Punkten den Weg mit der längsten Eigenzeit.

Gibt es Himmelskörper, deren Ausmaße vergleichbar mit dem Loch in der Trichterfläche sind oder sogar darunter liegen, sodass wir das Loch nicht mehr wegdiskutieren können? Bei normalen Sternen oder Planeten ist das nicht der Fall – so wäre das Loch bei der Sonne nur rund 6 km groß. Anders sieht die Sache aus, wenn ein Stern am Ende seines Lebens seinen Fusionsbrennstoff verbraucht hat und nicht mehr die notwendige Energie erzeugen kann, um sich der enormen Schwerkraft entgegenzustemmen. In diesem Fall kontrahiert sein Zentrum, während die äußeren Hüllen abgestoßen werden.

Bei Sternen wie unserer Sonne bleibt am Ende dieser Entwicklung das kontrahierte Sternenzentrum als weißer Zwerg zurück. Dieser ist nur noch etwa erdgroß und damit immer noch deutlich größer als das Loch in der Trichterfläche, obwohl in ihm die Masse des gesamten Sternenzentrums enthalten ist. Seine Stabilität erhält der weiße Zwerg durch einen quantenmechanischen Effekt: das Pauli-Prinzip, das verhindert, dass zwei Elektronen der Sternmaterie denselben quantenmechanischen Zustand einnehmen können.

Bei deutlich massereicheren Sternen wird die Gravitation allerdings so groß, dass die Elektronen gleichsam in die Protonen der Atomkerne hineingedrückt werden, wobei sich diese in Neutronen umwandeln. Das Sternenzentrum kollabiert dabei während einer Supernovaexplosion in Sekundenbruchteilen zu einem Neutronenstern, der nur noch rund 10 bis 20 Kilometer groß ist. Dieses extrem kompakte und massereiche Objekt ist nur noch wenig größer als das Loch in der Trichterfläche, sodass die Krümmung der Raumzeit in seiner Nähe deutlich spürbar wird. Die Gravitation an der Oberfläche eines Neutronensterns ist unvorstellbar groß und zerquetscht jede Form vom Materie.

Neutronensterne zeigen nun ein ungewöhnliches Verhalten: Je mehr Masse sie in sich vereinen, umso kleiner sind sie, denn umso stärker werden sie von der Gravitation zusammengedrückt. Das quantenmechanische Pauli-Prinzip für die Neutronen hat zunehmend Schwierigkeiten, den notwendigen Gegendruck zur Stabilisierung des Neutronensterns aufzubauen.

Bei ungefähr 3 Sonnenmassen unterschreitet die Größe des Neutronensterns schließlich die Größe des Lochs in der Trichterfläche, sodass die komplette Trichterfläche nun für die Raumkrümmung im Außenbereich des Neutronensterns wirksam wird. Nun können wir das Loch nicht mehr ignorieren – doch was bedeutet das für Raum und Zeit? Hat der Raum etwa ein Loch?

In gewissem Sinn hat er das tatsächlich! Der Neutronenstern kollabiert nämlich zu einem Schwarzen Loch, dessen Ereignishorizont durch den Lochrand in der Trichterfläche dargestellt wird. Der Ereignishorizont umschließt dabei wie eine Kugeloberfläche das Schwarze Loch, wobei man den Kugelradius als Schwarzschildradius bezeichnet. Nichts – auch Licht nicht – kann einem Schwarzen Loch entrinnen, wenn es einmal den Ereignishorizont überschritten hat. Der Raum im Inneren des Ereignishorizontes ist von außen nicht zugänglich.

Nun stellt die Trichterfläche den Raum dar, wie ihn ein Beobachter wahrnimmt, der außerhalb des Schwarzen Lochs bewegungslos ruht. Für einen solchen Beobachter hat der Raum tatsächlich ein Loch, also einen für ihn unzugänglichen Bereich. Allerdings wissen wir von oben, dass Raum und Zeit eng miteinander verwoben sind und dass man sie für ein umfassendes Bild zusammen betrachten muss. Dabei stellt sich heraus: Die Raumzeit hat nicht wirklich ein Loch. Es hängt vielmehr vom Beobachter ab, was von dieser Raumzeit erreichbar ist.

Ein bedauernswerter Astronaut in einem Raumschiff, das in das Schwarze Loch hineinfällt, bemerkt beim Überschreiten des Ereignishorizontes nichts Besonderes, d.h. für ihn gibt es kein Loch. Er weiß nicht, dass es nun keine Rückkehr für ihn mehr gibt, denn unterhalb des Ereignishorizonts vertauscht die radiale Abstandskoordinate zum Zentrum ihre Rolle mit der Zeit, sodass fortschreitende Zeit immer zum Zentrum hin führt. Astronaut und Raumschiff enden unweigerlich im Zentrum des Schwarzen Lochs, und nichts kann sie davor bewahren.

Von außen betrachtet bleibt die Zeit dagegen am Ereignishorizont stehen – jede Bewegung kommt dort zum Stillstand, und das Licht jedes Gegenstandes verblasst dort, denn es wird zu unendlich langen Wellenlängen rotverschoben. Ein Raumschiff, das in ein Schwarzes Loch fällt, wird also von außen gesehen am Ereignishorizont sehr schnell immer röter und dunkler und verschwindet so aus der Welt eines äußeren Beobachters. Den Übertritt ins Innere des Schwarzen Lochs kann man daher von außen gar nicht sehen!

Soviel zu Schwarzen Löchern. Kommen wir nun zurück zu einer unserer Ausgangsfragen, die wir im Licht der Allgemeinen Relativitätstheorie neu betrachten wollen: Wenn sich der Raum unter dem Einfluss von Materie krümmen kann, muss es dann nicht doch so etwas wie einen realen (absoluten, wenn auch veränderlichen) Raum geben? Was ist mit dem Relativitätsprinzip, das die Existenz eines solchen Raumes leugnet?

Die Sache ist kompliziert, aber ich möchte dennoch versuchen, zumindest grob das vollständige Bild zu skizzieren, das sich aus der Allgemeinen Relativitätstheorie ergibt:

Zunächst einmal muss man sich Raum und Zeit wieder vereint zu einer vierdimensionalen Raumzeit vorstellen, die von der Gravitation gekrümmt werden kann. Sie umfasst die Menge aller möglichen Ereignisse – also alle Raum-Zeit-Punkte. Jeder Beobachter besitzt nun seine eigenen Maßstäbe, mit denen er die Raumzeit mit einem Koordinatennetz aus drei Raum- und einer Zeitkoordinate überzieht. Im allgemeinen Fall wird dieses Koordinatennetz krummlinig sein, so wie das Netz aus Längen- und Breitengraden auf der Erdoberfläche krummlinig ist. Dabei werden – anders als bei den Inertialsystemen weiter oben – auch beschleunigte Beobachter und ihre Bezugssysteme mit betrachtet.

Es gibt nun in jedem Raum-Zeit-Punkt eine Gruppe besonderer Beobachter: Sie überlassen sich im freien Fall der Gravitation und durchlaufen dabei zu dem passenden Zeitpunkt den entsprechenden Raumpunkt. Nach Einsteins Äquivalenzprinzip, das wir im letzten Kapitel kennengelernt haben, gilt für diese Beobachter:

• Lässt man sich fallen, so spürt man die Gravitationskraft nicht.

Mit anderen Worten: In einer frei fallenden nichtrotierenden Raumkapsel herrscht Schwerelosigkeit, so als gäbe es keine Gravitation. Dabei versteht man unter freiem Fall, dass die Raumkapsel nicht durch Raketen beschleunigt wird oder auf dem Erdboden steht, sondern dass man sie im leeren Weltraum sich selbst überlässt. Sie kann dabei einen Stern umrunden, auf einen Planeten herabstürzen oder auch weit entfernt von allen Himmelskörpern gleichmäßig ihre Bahn ziehen.

Die Schwerelosigkeit in der frei fallenden Raumkapsel führt dazu, dass wieder Gesetze der Speziellen Relativitätstheorie gelten, so wie sie ein Beobachter in einem unbeschleunigten Inertialsystem ohne Schwerkraft wahrnimmt. Und damit kann man auch die Raumzeit innerhalb der Raumkapsel genau so beschreiben, wie man das in der Speziellen Relativitätstheorie tut, nämlich durch karthesische (also rechtwinklige) Raumkoordinaten und eine ungekrümmte Zeit, die beide über die Minkowskimetrik miteinander verknüpft sind.

Dabei darf die Raumkapsel aber nicht zu groß sein, denn sonst machen sich in ihr räumliche Unterschiede im Gravitationsfeld bemerkbar, die sich durch den freien Fall einer einzigen Raumkapsel nicht überall zugleich neutralisieren lassen. Daher kann man die Raumzeit immer nur lokal (also in einer kleinen Umgebung jedes Ereignisses) durch die ungekrümmten Raum- und Zeitkoordinaten der Speziellen Relativitätstheorie beschreiben.

Die Situation ist ganz ähnlich zu den Koordinaten auf einer Kugelfläche: Lokal kann man immer rechtwinklige Koordinaten einführen, so wie dies die Längen- und Breitengrade am Erdäquator tun, denn lokal sieht jede Fläche wie eine flache Ebene aus. Mit zunehmender Entfernung wird auf einer gekrümmten Fläche aber jedes Koordinatensystem krummlinig, denn dann machen sich die Abweichungen von der Ebene bemerkbar.

Was bedeutet es nun, dass die Raumzeit-Koordinaten in größerer Entfernung zu einer frei fallenden Raumkapsel krummlinig werden? Es bedeutet, dass aus Sicht der Raumkapsel andere weit entfernte Objekte, die ebenfall frei fallen, aus ihrer geradlinigen Bewegung abgelenkt werden – sie erscheinen beschleunigt. In weiter Entfernung sehen wir die Gravitation am Werk, die wir innerhalb der Raumkapsel nicht spüren.

Gekrümmte Raumzeit-Koordinaten bewirken also, dass frei fallende Objekte beschleunigt erscheinen. Genau das ist beispielsweise für einen Beobachter der Fall, der auf der Erdoberfläche steht. Sein Raumzeit-Koordinatensystem ist gekrümmt, da er sich nicht im freien Fall befindet. Dabei ist insbesondere seine Zeitkoordinate gekrümmt, denn weiter unten läuft die Zeit für diesen Beobachter langsamer als weiter oben. Frei fallende Objekte beschleunigen für ihn nach unten, und er selbst empfindet die Gravitation wie eine Scheinkraft, wie sie in einer beschleunigten Rakete im leeren Weltraum wirkt (Einsteins Äquivalenzprinzip).

Einstein sagt also:

• Bei Gravitation muss man die frei fallenden Bezugssysteme lokal als die Referenzsysteme ansehen, in denen keine Beschleunigung herrscht.

Frei fallende Bezugssysteme entsprechen damit den Inertialsystemen der speziellen Relativitätstheorie und liefern die Referenz, gegenüber der man Beschleunigungen oder auch Drehungen definiert. Stehen wir auf der Erdoberfläche, so sind wir in einem beschleunigten Bezugssystem, lassen wir uns dagegen frei fallen, so sind wir lokal in einem unbeschleunigten Bezugssystem. Newton hätte das noch genau umgekehrt ausgedrückt: Für ihn steht jemand unbeschleunigt auf der Erdoberfläche (die Erdrotation lassen wir mal außen vor), und ein frei fallendes Objekt beschleunigt aufgrund der Gravitationskraft. Dieser Wechsel in der Perspektive war die entscheidende Leistung, die Albert Einstein eine relativistische Beschreibung der Gravitation erst ermöglichte!

Was sagt diese Erkenntnis nun über das Relativitätsprinzip aus? Nach Ernst Mach konnte man die Bewegung eines Körpers ja immer nur relativ zu anderen Körpern angeben, aber niemals absolut. Nun haben nach Einstein alle Körper über die Gravitation einen Einfluss auf Raum und Zeit und bestimmen dadurch deren Struktur. Bedeutet das, dass Ernst Mach recht hatte?

Bis heute werden intensive Diskussionen zu diesem Thema geführt. Für Albert Einstein selbst war das Mach'sche Relativitätsprinzip ein wichtiger Leitfaden bei der Formulierung seiner Allgemeinen Relativitätstheorie. Später jedoch äußerte er sich eher kritisch zu den Ideen Ernst Machs. So ist es zwar richtig, dass Materie die Krümmung der Raumzeit bestimmt. Man kann aber gedanklich die Dichte der Materie immer kleiner werden lassen, bis diese verschwindet. Raum und Zeit verschwinden dadurch aber nicht, sondern es ergibt sich die flache Raumzeit der Speziellen Relativitätstheorie, in der sich beschleunigte und unbeschleunigte Bewegungen auch ohne Referenzobjekte gut unterscheiden lassen. Dies geht sogar in der Allgemeinen Relativitätstheorie – also mit Materie und ihrer Gravitation – da dort die frei fallenden Bezugssysteme als lokale Referenz für Beschleunigungen dienen. Es sieht also ganz so aus, als ob das Mach'sche Relativitätsprinzip zumindest in seiner strengen Form so nicht realisiert ist. Allerdings werden wir gleich sehen, dass Ernst Machs Idee wieder an Charme gewinnt, wenn wir das gesamte Universum in den Blick nehnem.

Die Raumzeit des Universums

In Einsteins Allgemeiner Relativitätstheorie sind Raum und Zeit selbst physikalische Objekte, die eng mit der in ihnen enthaltenen Materie verknüpft sind. Daher ist diese Theorie auch in der Lage, die Raumzeit des gesamten Universums physikalisch zu beschreiben, wobei man sich nicht für einzelne Sterne oder Galaxien interessiert, sondern für das Universum als Ganzes. Um ein übersichtliches Modell des Universums zu erhalten, nimmt man vereinfacht an, dass sich die Materie zumindest auf großen Skalen gleichmäßig im Universum verteilt, und dass es im Universum keine Vorzugsrichtungen gibt. Wenn man Raumvolumina von mehreren hundert Milliarden Lichtjahren Durchmesser betrachtet, so wird diese Annahme durch moderne Beobachtungen recht gut bestätigt.

Einstein war recht überascht, als er bei seinen Berechnungen im Jahr 1917 in diesem Modell herausfand, dass es kein statisches Universum zu geben schien: Entweder das Universum expandiert, wobei sich die darin enthaltenen Galaxien immer weiter voneinander entfernen, oder es kontrahiert und alle Galaxien rücken immer enger zusammen. Letztlich liegt die Ursache für dieses Verhalten darin begründet, dass die anziehenden Gravitationskräfte der Galaxien untereinander kein statisches Kräftegleichgewicht zulassen.

Nun war man damals aber allgemein der Ansicht, dass unser Universum statisch sein müsse. Einstein war daher sehr unzufrieden mit seinem Ergebnis und verwendete einen Trick, um doch noch ein statisches Universum zu erreichen: Er fügte seinen Gleichungen eine sogenannte kosmologische Konstante hinzu, die einer Materieform entspricht, die den Raum gleichmäßig durchdringt, ohne sich dabei jemals zu verdünnen oder anzureichern. Man kann sich diese Materieform wie eine Art unzerstörbare innere Raumenergie vorstellen, die dem Raum selbst innewohnt – eine solche lokalisierte Energie ist ja nach Einsteins Formel \( E = m c^2 \) von Masse nicht unterscheidbar, sodass wir hier die Begriffe Materie bzw. Masse und Energie teilweise synomym verwenden.

Wie aber kann es sein, dass sich eine Raumenergie bei der Expansion des Raums nicht verdünnt? Wo kommt die fehlende Raumenergie her? Die Lösung lautet: Eine solche Materieform muss einen negativen Druck aufweisen, d.h. sie unterliegt starken inneren Zugkräften, die gleichmäßig in alle Richtungen wirken – ähnlich wie bei einer straff gespannten Gummihaut. Will man eine solche Gummihaut gegen die inneren Zugkräfte auseinanderziehen, so muss man dafür Energie aufwenden. Analog muss man Energie zuführen, wenn sich ein Raum mit überall vorhandener innerer Raumenergie ausdehnt. Diese Energie manifestiert sich als innerer Raumenergie im größer gewordenen Raum.

Aus dem letzten Kapitel wissen wir, dass nach Einsteins Gravitationsgesetz negativer Druck eine abstoßende Gravitation bewirkt. Die kosmologische Konstante – also die innere Raumenergie – bewirkt daher über größere Raumabstände hinweg eine zunehmend abstoßende Gravitationskraft, die der anziehenden Gravitation der sonstigen Materie entgegenwirkt und so ein Kräftegleichgewicht ermöglicht. Ein statisches Universum erschien möglich, und Einstein war zufrieden – zumindest vorerst.

Er hatte allerdings einen wichtigen Punkt übersehen – ein bemerkenswerter Fehler bei einem so herausragenden Genie, wie Einstein es unzweifelhaft war: Das Kräftegleichgewicht zwischen Anziehung und Abstoßung ist instabil! Wird es nur ein wenig gestört, so gewinnt entweder die Anziehung oder die Abstoßung die Oberhand. Wenn sich nämlich das Universum beispielsweise leicht ausdehnt, so verdünnt sich die normale Materie aus Sternen, Galaxien etc. und ihre Anziehung nimmt ab. Die innere Raumenergie verdünnt sich jedoch nicht, denn sie entspricht einer inneren Eigenschaft des Raumes selbst. Ihre Abstoßung bleibt also unvermindert bestehen und treibt das Universum weiter auseinander.

Man kann fast sagen, dass Einstein den Vorhersagen seiner eigenen Theorie mistraute und versuchte, sie durch Einfügen seiner kosmologischen Konstante den damals vorherrschenden Ansichten anzupassen und so ein statisches Universum zu erzwingen. Andere Physiker wie Alexander Friedmann im Jahr 1922 und Georges Lemaître 1927 erkannten dagegen, dass Einsteins Gleichungen nur ein dynamisches Universum zuließen. Schließlich zeigten Beobachtungen von Vesto Slipher und Edwin Hubble, dass die Wellenlängen im Licht ferner Galaxien umso stärker gedehnt sind, je weiter entfernt die Galaxien von uns sind. Damit war klar, dass unser Universum gar nicht statisch ist! Auf dem langen Weg des Lichts von einer fernen Galaxie bis zu uns dehnt sich der Raum ständig aus, wodurch auch die Wellenzüge des Lichts gedehnt werden. Das Licht wird dadurch zu längeren Wellenlängen hin rotverschoben.

In einem expandierenden Universum wachsen die Abstände der Galaxien zu uns ständig an – und zwar umso stärker, je größer der jeweilige Abstand bereits ist. Die Galaxien selbst bewegen sich dabei kaum; es ist der Raum zwischen ihnen und uns, der sich ausdehnt. Man kann sich die Galaxien wie Punkte auf einem Luftballon vorstellen, den man aufbläst: Die Punkte selbst bewegen sich nicht, aber der Abstand zwischen ihnen entlang der Gummihaut wächst. Dabei entspricht die zweidimensionale Gummihaut unserem Universum und nicht das Balloninnere.

Als klar war, dass sich unser Universum ständig ausdehnt, verwarf Einstein seine kosmologische Konstante und soll sie als "größte Eselei seines Lebens" bezeichnet haben. Es gab keinen Grund mehr für eine solche Konstante und die zugehörige exotische innere Raumenergie. Und dennoch: Grundsätzlich ist eine soche Konstante in der Allgemeinen Relativitätstheorie möglich, und sie wird weiter unten auf wundersame Weise wiederauferstehen!

Unser Universum dehnt sich also aus, und Galaxien entfernen sich voneinander, wenn ihre Abstände groß genug sind, sodass die anziehende Gravitation zwischen ihnen gegen die Raumexpansion nicht mehr ankommt. Bei den Galaxien in unserer Nachbarschaft ist das noch nicht der Fall. Wenn wir jedoch 100 Millionen Lichtjahre und mehr hinausblicken, so macht sich die Raumexpansion zunehmend bemerkbar. Die heutige Expansionsrate des Universums – auch Hubble-Parameter oder Hubble-Konstante genannt – liegt bei rund 72 km/s pro Megaparsec (etwa 3,26 Millionen Lichtjahre). Bei einer Galaxie in 100 Millionen Lichtjahren Abstand zu uns wächst dieser Abstand mit einer Geschwindigkeit von rund 2200 km/s an – das ist bereits deutlich mehr als die typische Eigenbewegung von Galaxien, die bei wenigen hundert km/s liegt.

Man kann die heutige Expansionsrate des Universums auch etwas anschaulicher so ausdrücken: In einer Milliarde Jahren wachsen große Abstände im Universum um etwa 7,4 Prozent an. Wenn wir nun die Expansion des Universums rückwärts in der Zeit betrachten, so rücken alle Galaxien immer enger zusammen, da der Raum zwischen ihnen schrumpft. Es wäre wie bei der Hülle eines Luftballons, aus dem man die Luft herauslässt. Wie lange würde es bei unserem Blick in die Vergangenheit dauern, bis die Abstände aller Galaxien auf Null geschrumpft sind?

Das hängt natürlich davon ab, wie sich die Expansionsrate des Universums – also der Hubble-Parameter – mit der Zeit verändert. Wenn diese Rate zeitlich konstant wäre, dann würden die Galaxienabstände umso langsamer schrumpfen, je kleiner sie sind, und sie würden nie wirklich auf Null zurückgehen. Das Universum könnte demnach unendlich alt sein! Doch die Expansionsrate war in der Vergangenheit nicht konstant. Die anziehende Wirkung der Gravitation hat insbesondere in der Anfangszeit des Universums die Expansionsrate schrumpfen lassen – sie war also damals größer als heute.

Nehmen wir vereinfacht an, dass sich alle Galaxienabstände bei unserem Blick rückwärts in der Zeit mit ihrer heutigen Geschwindigkeit verringern, sodass sie pro einer Milliarde Jahre etwa 7,4 Prozent ihrer heutigen Größe verlieren. Das entspricht einer Expansionsrate, die umso größer ist, je weiter wir in der Zeit zurückgehen. Wie lange dauert es dann, bis 100 Prozent erreicht sind und alle Abstände damit auf Null geschrumpft sind? Das ist nicht schwer auszurechnen: 100 Prozent geteilt durch 7,4 Prozent ergibt rund 13,5 – es sind also etwa 13,5 Milliarden Jahre.

Genauere Analysen, die die Wirkung der Gravitation noch besser berücksichtigen, sowie moderne Beobachtungen zeigen: Unser Universum hat seinen Lebensweg vor 13,8 Milliarden Jahren mit einem Zustand extrem hoher Dichte und Temperatur begonnen. Diesen Anfangszustand bezeichnet man als Urknall. Seidem dehnt sich das Universum aus. Dabei sollte die anziehende Gravitation zwischen den auseinanderstrebenden Materieteilchen diese Ausdehnung immer weiter abgebremst haben – so würde man es zumindest erwarten.

Um diese Abbremsung der Expansion zu belegen, beobachteten zwei Forschergruppen (das Supernova Cosmology Project, kurz SCP, sowie das High-z Supernova Search Project, kurz High-z SS) in den 1990er Jahren unabhängig voneinander die Helligkeit weit entfernter thermonuklearer Supernovae. Bei diesen Supernovae gerät ein ausgebranntes Sternenzentrum – ein weißer Zwerg – nach Aufsammeln weiterer Materie in einen instabilen Zustand und beginnt zu kollabieren. Dabei zündet er eine nukleare Kettenreaktion in seinem Inneren, die ihn in einer gewaltigen Explosion komplett zerreißt. Diese Sternen-Atombomben sind über sehr weite Entfernungen hin sichtbar, und da sie immer ungefähr gleich hell sind, lässt sich ihre heutige Entfernung aus ihrer bei uns sichtbaren Helligkeit recht gut bestimmen. Zugleich kann man aus der Rotverschiebung ihres Lichts die Raumausdehnung seit der Explosion ermitteln und so letztlich die Expansionsgeschichte der Universums rekonstruieren.

Im Jahr 1998 veröffentlichten die beiden Forschungsgruppen ihre Ergebnisse: In den ersten rund neun Milliarden Jahren seit dem Urknall hat sich die Expansion tatsächlich wie erwartet verlangsamt. In den letzten fünf Milliarden Jahren jedoch hat sich die Expansionsrate einem konstanten Wert angenähert, sodass die Abstände zwischen den Galaxien seitdem umso schneller anwachsen, je größer sie werden! Das Universum dehnt sich also mittlerweile nahezu exponentiell aus, und man spricht von einer beschleunigten Expansion!

Man kann sich vorstellen, was für eine enorme Aufregung diese Veröffentlichung hervorrief! Weitere Beobachtungen haben die beschleunigte Expansion seitdem immer genauer bestätigt, und im Jahr 2011 bekamen die beiden Forschergruppen für ihre Entdeckung den Physik-Nobelpreis verliehen. Aber was um Himmels Willen könnte eine beschleunigte Expansion hervorrufen? Vielleicht ahnen Sie es schon: Einsteins totgeglaubte kosmologische Konstante – in der obigen Grafik als dunkle Energie bezeichnet – erblickt erneut das Licht der Welt.

Doch gehen wir der Reihe nach vor und schauen uns zunächst an, was man über die Materie im Universum aus vielen Beobachtungen heute weiß. Der erste Schritt auf diesem Weg liegt in der Erkenntnis, dass die mittlere Raumkrümmung im Universum alleine durch seine mittlere Materiedichte bestimmt wird. Dabei gibt es eine kritische Dichte, bei der die Raumkrümmung Null wird. Im Kleinen, also in der Nähe großer Massenansammlungen, wird der Raum natürlich auch dann weiter leicht gekrümmt sein. Im Großen jedoch mitteln sich diese Krümmungen gegenseitig weg und der Raum wird euklidisch flach. Die kritische Dichte liegt bei rund 6 Protonmassen pro Kubikmeter – alles, was es an Materie und Energie im Universum gibt, muss also zusammen diese mittlere Dichte ergeben, damit das Universum im Großen flach wird.

Liegt die Dichte darüber, so ist das Universum positiv gekrümmt und nimmt die Form der 3-Sphäre an, die wir oben bereits kennengelernt haben. Die 3-Sphäre war das dreidimensionale Analogon der Kugeloberfläche. Sie besitzt zwar keinen Rand, aber dennoch ein endliches Raumvolumen. Ein solches Universum wäre also unbegrenzt und zugleich endlich.

Liegt die Dichte dagegen unter der kritischen Dichte, so ist das Universum negativ gekrümmt, ähnlich wie eine zweidimensionale Sattelfläche. In diesem Fall wäre der Raum unendlich – ebenso wie bei einem flachen Universum.

Vielleicht ist es etwas überaschend, dass der Raum flach sein kann, obwohl Materie in ihm vorhanden ist – müsste diese nicht den Raum in jedem Fall krümmen? Die Verwirrung entsteht, weil wir die Zeit vergessen haben: Materie krümmt nicht den Raum alleine, sondern die Raumzeit insgesamt. Bei der kritischen Dichte ist zwar der Raum flach, aber die Zeit ist gekrümmt, was sich in der Expansion des Universums äußert. Uhren in weit entfernten Galaxien laufen daher aus unserer Sicht langsamer, denn ihre Zeitsignale werden auf ihrem Weg zu uns durch die Raumexpansion auseindergezogen.

Zurück zur Raumkrümmung: Da mittlere Materiedichte und mittlere Raumkrümmung im Universum eindeutig miteinander zusammenhängen, müsste es doch möglich sein, die mittlere Krümmung des Universums zu messen und so seine mittlere Materiedichte zu bestimmen. Doch wie können wir diese mittlere Krümmung messen? Wir sind ja nicht an der Raumkrümmung im Schwerefeld der Erde, der Sonne oder der Milchstraße interessiert, sondern an der mittleren Raumkrümmung auf Skalen von hunderten oder gar tausenden von Millionen Lichtjahren, auf denen wir die Materieverteilung als annähernd homogen ansehen können.

Die Lösung lautet: Wir brauchen dazu sehr große Dreiecke im Universum, bei denen wir die Kantenlängen bzw. Winkel gut genug kennen. Und wir haben Glück: Seit dem Jahr 2003 ist es gelungen, solche Dreiecke präzise genug zu vermessen, um die mittlere Krümmung des Universums aufzuspüren. Es sind die größten Dreiecke, die sich mit elektromagnetischen Strahlen bilden lassen, denn sie reichen so weit ins Universum hinaus, wie wir mit elektromagnetischer Strahlung überhaupt schauen können: bis zur Entstehung der kosmischen Hintergrundstrahlung!

Die kosmische Hintergrundstrahlung ist eine sehr schwache Mikrowellen-Wärmestrahlung mit einer Temperatur von rund 2,7 Kelvin, die unser Universum durchdringt. Sie erreicht uns von jeder Stelle des Nachthimmels, und sie ist uralt, denn sie entstand nur 380000 Jahre nach dem Urknall. Das Universum war damals von einem dünnen, heißen Plasma aus Wasserstoff und Helium durchdrungen, das bei rund 3000 Kelvin gelb-rötlich glühte. Sterne oder andere Himmelskörper gab es noch nicht. Beim Unterschreiten der 3000 Kelvin verwandelte sich nun das glühende Plasma in durchsichtiges Wasserstoff-Helium-Gas, welches das Licht und die Wärmestrahlung des Plasmas freigab, sodass diese seitdem ungehindert das Universum durchqueren kann. Bis heute hat sich das Universum seitdem um gut das Tausendfache ausgedehnt, sodass die Temperatur der Wärmestrahlung um denselben Faktor gefallen ist.

Wenn wir also mit empfindlichen Mikrowellendetektoren in den schwarzen Himmel schauen, so sehen wir ganz weit draußen überall das glühende Plasma in dem Moment, als es durchsichtig wurde. Sein Licht ist durch die Raumexpansion auf seinem Weg zu uns um das Tausendfache bis in den Mikrowellenbereich rotverschoben.

Nun erscheint die Temperatur des Plasmas nicht überall ganz gleichmäßig. In einer bestimmte Himmelsrichtung sieht die kosmische Hintergrundstrahlung etwas heißer, in der Gegenrichtung etwas kühler aus. Das liegt daran, dass sich unser Sonnensystem mitsamt der Erde mit rund 270 km/s gegenüber der Hintergrundstrahlung bewegt. In Flugrichtung erscheint die Wellenlänge von der Erde aus gesehen daher etwas gestaucht, in der Gegenrichtung dagegen etwas gedehnt – man spricht hier vom Dopplereffekt.

Als mir dieser Effekt zum ersten Mal begegnete, war ich sehr überascht, denn er bedeutet, dass es im Universum ein ausgezeichnetes Bezugssystem gibt, gegenüber dem man absolute Geschwindigkeiten angeben kann. Nach dem, was ich über die Gleichwertigkeit von Inertialsystemen wusste, hatte ich so etwas nicht erwartet! Aber auch hier muss man zur Geschwindigkeitsmessung aus dem Fenster schauen und die kosmische Hintergrundstrahlung beobachten, sodass Einsteins Relativitätsprinzip weiterhin gilt.

Man kann mithilfe des Dopplereffekts sogar genau sagen, wann ein Objekt im Universum ruht – zumindest relativ zur Hintergrundstrahlung. In genau diesem Sinne hatten wir oben davon gesprochen, dass sich Sterne und Galaxien im Universum auf großen Skalen betrachtet kaum bewegen, und dass es der Raum selber ist, der sich ausdehnt. Die relativ geringe Eigenbewegung der Sterne gegenüber der Hintergundstrahlung ist nicht besonders überraschend, denn Hintergrundstrahlung und Sternenmaterie waren ja einst im glühenden Plasma eng miteinander verkoppelt. Die heutigen Galaxienbewegungen von wenigen hundert km/s gegenüber der Hintergrundstrahlung entstanden erst im Lauf der Zeit aufgrund der Gravitation, die diese Galaxien langsam zu größeren Galaxienhaufen zusammenzog. Über hunderte von Lichtjahren gemittelt liefern Galaxien und Hintergrundstrahlung praktisch dasselbe Bezugssystem für Bewegungen. Ernst Mach hätte sich sicher darüber gefreut!

Wenn man nun den Effekt durch die Eigenbewegung der Erde herausrechnet, ist dann die kosmische Hintergrundstrahlung überall am Himmel genau gleich warm – oder besser gleich kalt? Das ist tatsächlich fast exakt der Fall, aber eben nicht ganz: Es gibt Flecken unterschiedlicher Größe am Himmel, die geringfügig heißer oder kälter sind, wobei diese Schwankungen nur wenige Tausendstel Prozent betragen. Solche Schwankungen muss es auch geben, denn sie spiegeln die geringen Dichteschwankungen im heißen Plasma 380000 Jahre nach dem Urknall wider, die später als Keimzelle für das Zusammenziehen der Materie zu Sternen und Galaxien dienen. Seit dem Jahr 2003 ist es mit den Satelliten WMAP und neuerdings Planck gelungen, diese Temperaturflecken im Detail zu vermessen und eine genaue Himmelskarte der kosmischen Hintergrundstrahlung zu erstellen:

Schaut man sich die statistische Größenverteilung der Temperaturflecken an, so findet man eine Häufung bei bestimmten Winkelgrößen am Himmel. Die größten häufiger vorkommenden Flecken messen dabei etwa ein Winkelgrad am Himmel – das sind rund zwei Vollmonddurchmesser.

Die Ausmaße dieser größeren Flecken entsprechen nun ungefähr der Strecke, die ein Signal vom Urknall bis zur Freigabe der Hintergrundstrahlung 380000 Jahre später im expandierenden Plasma zurückgelegt haben kann. Der Rand eines solchen Temperaturflecks entspricht damit grob dem damaligen Rand desjenigen sichtbaren Universums, das von der Fleckenmitte 380000 Jahre nach dem Urknall physikalisch zugänglich war. Das Wort sichtbar ist dabei so zu verstehen: Wäre das Universum seit dem Urknall durchsichtig gewesen, so wäre dieser Rand die Grenze, bis zu der man damals maximal vom Fleckenmittelpunkt hätte schauen können. Alle physikalischen Signale, die seit dem Urknall jenseits dieses Randes ausgesendet wurden, hätten noch keine Zeit gehabt, den Mittelpunkt zu erreichen. Wir sehen also im Muster der großen Flecken am Himmel sehr schön, wie sich der expandierende Raum damals in viele einzelne Raumbereiche aufteilte, die seit dem Urknall noch keinen Kontakt zueinander gehabt haben können.

Das ist auch heute noch so: Jeder Raumpunkt hat zu jeder Zeit sein eigenes sichtbares Universum. Dabei zeigt das Fleckenmuster, dass das gesamte Universum sehr viel größer sein kann als der Teil, zu dem man Zugang hat – damals war es zumindest so, und es gibt keinen Grund, dass das heute anders sein sollte. Weiter unten werden wir uns das noch genauer ansehen.

Man kann nun ziemlich genau ausrechnen, wie groß die Temperaturflecken damals gewesen sein müssen. Außerdem weiß man recht genau, wie weit sie entfernt sind. Nun muss man sich nur noch ansehen, wie groß die Flecken am Himmel erscheinen, und man hat die entsprechenden Sicht-Dreiecke zusammen, die wir zur Bestimmung der Raumkrümmung des Universums brauchen. Die eine Seite eines solchen Dreiecks bildet dabei der Durchmesser eines Temperaturflecks, und die anderen beiden Seiten sind die Sichtlinien bis zu uns.

Je nach Raumkrümmung hat nun ein solches Dreieck eine etwas andere Gestalt, denn die beiden Sichtlinien sind in einem gekrümmten Raum ebenfalls gekrümmt. Anders ausgedrückt: Die Temperaturflecken erscheinen uns je nach Raumkrümmung des Universums am Himmel unterschiedlich groß.

Wie groß muss die Raumkrümmung nun sein, damit die sichtbare Fleckengröße mit der berechneten Größe übereinstimmt? Mit hoher Genauigkeit kommt heraus: Die mittlere Krümmung des Universums ist Null, d.h. unser Universum muss insgesamt flach oder zumindest nahezu flach sein. Und damit muss die mittlere Dichte aller Materie im Universum gleich oder fast gleich der kritischen Dichte sein.

Nun liefert die mittlere Raumkrümmung des Universums lediglich die Summe aller Materiedichten im Universum. Sie sagt noch nichts darüber aus, wie sich diese Materie zusammensetzt. Um das herauszufinden, muss man viele weitere Beobachtungsgrößen hinzunehmen und sie zu einem konsistenten Gesamtbild zusammensetzen. So hilft beispielsweise das Verhältnis von Wasserstoff zu Helium dabei, die Dichte aller Atome im Universum zu bestimmen. Etwa 25 Gewichtsprozent der atomaren Materie im Universum bestehen aus Helium, das in den ersten Minuten nach dem Urknall entstanden ist. Der Rest ist zu fast 75 Gewichtsprozent Wasserstoff mit einer kleinen Beimischung von 1 bis 2 Gewichtsprozent aus schwereren Elementen.

Als Ergebnis kommt heraus: Die gesamte aus Atomen bestehende Materie im Universum ergibt nur 5 Prozent der kritischen Dichte. Nur ein Zwanzigstel aller Materie im Universum besteht also aus Atomen, und lediglich ein Zehntel dieser Atome können wir überhaupt sehen, da sie – beispielsweise in Form von Sternenmaterie – Licht aussendet. Der Rest der Atome befindet sich als sehr dünnes diffuses Gas im riesigen Raum zwischen den Galaxien.

Was ist mit den restlichen 95 Prozent? Photonen oder Neutrinos kommen hier nicht in Frage, da ihr Beitrag viel zu gering ist. Wir müssen daher zugeben, dass wir es nicht genau sagen können. Sehr viele Hinweise deuten jedoch konsistent darauf hin, dass es große Mengen sogenannter dunkler Materie geben muss, die nicht aus Atomen bestehen kann. Vermutlich setzt sie sich aus schweren noch unbekannten Elementarteilchen zusammen, die kaum mit der übrigen Materie wechselwirken und die wie Tröpchen eines unsichtbaren Nebels im Raum umherwabern. Am Large Hadron Collider LHC wird man in den nächsten Jahren intensiv versuchen, die Teilchen der dunklen Materie zu erzeugen und nachzuweisen.

Die dunkle Materie macht sich über ihre anziehende Gravitationswirkung deutlich im Universum bemerkbar. Sie bildet riesige Wolken, die mit ihrer Gravitation ganze Galaxien einfängt und sie zu großen Galaxienhaufen vereint. Man kann sich die Galaxien fast wie die Schaumkrönchen auf dem Wolkenmeer der dunklen Materie vorstellen. Aus der Gravitationswirkung lässt sich abschätzen, dass die dunkle Materiedichte insgesamt rund 25 Prozent der kritischen Dichte beträgt.

Atome und dunkle Materie ergeben zusammen damit rund 30 Prozent der kritischen Dichte – es fehlen also immer noch 70 Prozent! Es muss diese Materie geben, denn sonst wäre das Universum nicht flach. Doch was könnte sich dahinter verbergen?

Das ist der Moment, an dem wir uns an wieder an Einsteins kosmologische Konstante erinnern müssen: Oben haben wir gesehen, dass das Universum seit 5 Milliarden Jahren zunehmend beschleunigt expandiert. Es muss also eine weitere Materieform geben, die mit ihrer abstoßenden Gravitationswirkung das Universum auseinandertreibt. Dieser Materieform hat man den Namen dunkle Energie gegeben, ohne dass irgend jemand heute schon wüsste, was sich dahinter genau verbirgt. Man nimmt heute an, dass die dunkle Energie als eine Art innere Raumenergie den Raum gleichmäßig durchdringt, ohne bei der Expansion verdünnt zu werden. Daher muss sie einen negativen Druck besitzen und gravitativ abstoßend wirken.

Das Gesamtbild – flaches Universum mit kritischer Materiedichte, davon heute 5 % Atome, 25 % dunkle Materie und 70 % dunkle Energie – hat sich als sehr erfolgreich erwiesen und ist mittlerweile zum Standardmodell der Kosmologie aufgestiegen. Es scheint alle heute messbaren Eigenschaften des Universums sehr gut reproduzieren zu können. Jetzt müssen wir nur noch herausfinden, was sich hinter der dunklen Materie und der mysteriösen dunklen Energie wirklich verbirgt!

Mit diesem Modell kann man die Expansion des Universums seit dem Urknall gut nachvollziehen und auch für die weitere Zukunft modellieren (sofern unsere Annahme richtig ist, dass eine konstante dunkle Energie die zukünftige Expansion bestimmt). Damit lässt sich eine Übersichtskarte der gesamten bekannten Raumzeit zeichnen. Dazu lassen wir wieder zwei der drei Raumdimensionen weg und verwenden die x-Achse für den Abstand zu uns, während wir die y-Achse für die verstrichene Zeit nach dem Urknall verwenden. In dieses Diagramm tragen wir nun die Weltlinien der nahezu ruhenden Objekte im Universum ein, also beispielsweise den Weg der Sterne durch Raum und Zeit.

Die Grafik, die sich so zunächst ergibt, ist allerdings aufgrund der Raumexpansion noch ziemlich unübersichtlich. Nach unten hin drängen sich alle Linien immer mehr zur y-Achse hin zusammen, denn die Abstände zwischen den Objekten schrumpfen ja zum Urknall hin immer mehr gegen Null. Daher ist es besser, die Grafik so abzuändern, dass die Weltlinien der Materie senkrecht nach oben laufen, so als ob es keine Raumexpansion gäbe (die geringe Eigenbewegung der Materie im Raum können wir bei den hier betrachteten riesigen Entfernungen getrost vernachlässigen). Man sagt auch, dass man die mitbewegte Entfernung einträgt. Damit man aber trotzdem die echte Entfernung aus dem Diagramm ablesen kann, tragen wir rechts den Skalenfaktor \( a \) des Universums zur jeweiligen Zeit ein. Dieser Faktor kennzeichnet die Ausdehnung des Universums relativ zu heute, d.h. mit diesem Faktor müssen wir die eingetragene mitbewegte Entfernung multiplizieren, um die echte Entfernung zur jeweiligen Zeit zu ermitteln. Zum Urknall hin schrumpft der Skalenfaktor natürlich gegen Null, wärend er in der Gegenwart gleich Eins ist und aufgrund der beschleunigten Expansion in der Zukunft immer weiter anwächst.

Auch die Zeitachse wollen wir abändern: Wir tragen die Zeit nicht gleichmäßig ein, sondern wir stauchen sie nach oben hin immer mehr zusammen, sodass wir auch die unendlich ferne Zukunft noch eintragen können. Dabei können wir es so einrichten, dass sich Licht immer entlang von Diagonalen in der Grafik ausbreitet. Das macht es beispielsweise einfacher, Raumzeitbereiche voneinander abzugrenzen, die keinen Kontakt zueinander gehabt haben können.

Man kann nun sehr viel aus dieser Grafik über unser Universum lernen. Als erstes wird klar, dass ein Blick in die Ferne zugleich ein Blick zurück in der Zeit ist, denn das Licht eines fernen Ereignisses benötigt ja Zeit, um bis zu uns zu gelangen. Wir sehen in der Gegenwart alle diejenigen Ereignisse im Universum, die sich auf dem rot eingezeichneten Lichtkegel befinden. Dieser Lichtkegel verläuft von unserem heutigen Raum-Zeit-Punkt aus diagonal nach rechts unten und kennzeichnet den Weg, den das Licht in Raum und Zeit zurückgelegt hat, um uns hier und heute zu erreichen.

Dabei wurde das Licht auf dem Weg zu uns gedehnt und somit rotverschoben. Ein Beispiel: Wenn das Universum beim Aussenden des Lichts den Skalenfaktor \( a = 0,5 \) aufwies, so verlängert sich die Wellenlänge des Lichts bis zu seinem Eintreffen bei uns um den Faktor \( 1/a = 2 \), da sich der Raum seitdem bis heute um das 2-Fache ausgedehnt hat (nämlich vom damaligen Skalenfaktor \( a = 0,5 \) auf den heutigen Skalenfaktor \( a = 1 \) ). Meist verwendet man statt des Dehnungsfaktors \( 1/a \) des Lichts dessen Rotverschiebung \( z \), die angibt, welcher Anteil zur Wellenlänge hinzukekommen ist. So bedeutet \( z = 0,2 \) beispielsweise, dass die Wellenlänge um 20 % auf das 1,2-fache angewachsen ist. Für \( a = 0,5 \) haben wie also \( z = 1 \) (denn die Wellenlänge hat sich um 100 % auf das Doppelte verlängert). Allgemein gilt \( z = 1/a - 1 \) oder umgestellt \( z + 1 = 1/a \). Diese Rotverschiebung, die wir heute für verschiedene Ereignisse sehen, ist am oberen Rand der Grafik angegeben. Das ist sehr nützlich, denn meist geben Astronomen nicht die heutige Entfernung, sondern die gemessene Rotverschiebung für kosmische Objekte an. Diese können wir mitfilfe der Grafik direkt in eine Entfernung umrechnen. Für die kosmische Hintergrundstrahlung haben wir beispielsweise ungefähr \( z = 1000 \) und damit eine heutige Entfernung der entsprechenden Materie von rund 45 Milliarden Lichtjahren. Für die entferntesten heute beobachtbaren Galaxien messen wir dagegen Rotverschiebungen von etwa \( z = 10 \), was einer heutigen Entfernung von rund 30 Milliarden Lichtjahren entspricht.

Es herrscht viel Verwirrung, wenn man über den Entfernungsbegriff im Universum spricht. Oft wird einfach die Lichtlaufzeit in Lichtjahre übersetzt – dann wäre das Plasma, das die kosmische Hintergrundstrahlung 380000 Jahre nach dem Urknall ausgesendet hat, rund 13,8 Milliarden Lichtjahre von uns entfernt. Aus dem Plasma, dessen kosmische Hintergrundstrahlung wir heute am Himmel sehen, sind in der Zwischenzeit aber längst Galaxien entstanden, die heute aufgrund der Raumexpansion rund 45 Milliarden Lichtjahre von uns entfernt sind. Sehen können wir diese Galaxien allerdings nicht, denn ihr heute ausgesendetes Licht ist noch lange nicht bei uns eingetroffen – und wird dies wohl auch niemals schaffen, wie wir noch sehen werden. Die echte Entfernung der Materie können wir also nicht direkt beobachten, sondern nur im Expansionsmodell ausrechnen. Man müsste die Expansion des Universums schon anhalten, um die echte Entfernung anhand von Lichtlaufzeiten wirklich messen zu können.

In der Grafik ist nur der heutige Lichtkegel eingezeichnet. Wir könnten aber auch die Lichtkegel zu anderen Zeiten einzeichnen und damit die Ereignisse markieren, deren Licht wir früher sehen konnten oder in der Zukunft noch sehen werden. Im Lauf der Zeit verschiebt sich dabei dieser Lichtkegel immer weiter nach oben und überstreicht damit alle Ereignisse, deren Licht uns bis zu diesem Zeitpunkt irgendwann erreicht hat. Der Schnittpunkt des Lichtkegels mit der x-Achse gibt dann die am weitesten entfernten Objekte an, bis zu denen wir zu dieser Zeit im Universum schauen können, wobei wir die jeweils aktuelle Entfernung des entsprechenden Objekts meinen, dessen damaliges Licht wir sehen. Man nennt diese Entfernung auch Beobachtungshorizont, Teilchenhorizont oder Partikelhorizont. Dieser Horizont begrenzt das für uns zu dieser Zeit sichtbare, grundsätzlich irgendwie beobachtbare Universum. Er liegt heute in rund 45 Milliarden Lichtjahren Entfernung, d.h. alle Materie, deren Licht uns bis heute erreichen konnte, kann gegenwärtig nicht weiter als rund 45 Milliarden Lichtjahre von uns entfernt sein.

In der Vergangenheit war das sichtbare Universum deutlich kleiner als heute. Wir erinnern uns: Als die kosmische Hintergrundstrahlung 380000 Jahre nach dem Urknall entstand, war das von einem Punkt aus sichtbare Universum nur so groß wie die größeren Temperaturflecken, die wir heute in der Hintergrundstrahlung sehen. Der Raum selber endete aber keineswegs an diesem damaligen Beobachtungshorizont, und wir können ziemlich sicher sein, dass er auch an seinem heutigen Beobachtungshorizont in rund 45 Milliarden Lichtjahren Entfernung nicht endet. Hinter dem Horizont geht's weiter! Wie weit, kann heute niemand sagen. Der Raum könnte tatsächlich sogar unendlich groß sein, falls er gar keine oder eine winzige negative Krümmung aufweist. Falls er eine sehr kleine positive Krümmung besitzen sollte, dann wäre er wie die 3-Sphäre endlich, wobei unser sichtbares Universum wohl nur einen winzigen Ausschnitt dieses Raums erfasst – ähnlich wie ein kleiner Vorgarten kaum erahnen lässt, wie groß die Erdoberfläche tatsächlich ist.

Nun wird das sichtbare Universum im Laufe der Zeit immer größer, d.h. das Licht immer entfernterer Objekte kann uns irgendwann erreichen. Bedeutet das, dass jedes im Universum ausgesendete Licht uns irgendwann erreichen wird, wenn wir nur lange genug warten?

In einem Universum mit beschleunigter zukünftiger Expansion, so wie wir es in der Grafik voraussetzen, ist das nicht der Fall, denn der Lichtkegel nähert sich im Lauf der Zeit immer mehr einer Grenze an, die in der Grafik als grüner Ereignishorizont eingezeichnet ist. Ereignisse außerhalb dieses Ereignishorizonts werden wir niemals sehen können, denn der Raum dehnt sich schneller aus, als das Licht ihn überwinden kann. Heute liegt dieser Ereignishorizont in rund 16 Milliarden Lichtjahren Entfernung. Galaxien, die momentan weiter als 16 Milliarden Lichtjahre entfernt sind, werden wir also niemals in ihrem heutigen oder zukünftigen Zustand sehen können.

Es werden sogar immer mehr heute noch sichtbare Galaxien aus unserem Blickfeld verschwinden, oder genauer gesagt: Ihr Licht wird immer stärker rotverschoben und verblassen, wenn die Weltlinien dieser Galaxien den Ereignishorizont nach oben durchbrechen. Vollkommen unsichtbar wird eine Galaxie dabei streng genommen zwar nie, aber ihr Licht wird irgendwann so energiearm sein, dass es sich nicht mehr beobachten lässt. Genau dasselbe sieht übrigens auch ein Beobachter außerhalb eines schwarzen Lochs bei einem Objekt, das in das schwarze Loch hineinfällt und dabei den zugehörigen Ereignishorizont überquert.

In ferner Zukunft wird es also wohl sehr einsam im Universum werden. Alle Galaxien, deren Abstand zu uns anwächst, überschreiten irgendwann den Ereignishorizont. Man wird von uns aus dann weder diese Galaxien noch die kosmische Hintergrundstrahlung mehr wahrnehmen können, und alle beobachtbaren Hinweise auf die Expansion unseres Universums werden damit verschwunden sein. Eine paradoxe Situation, die beispielsweise Lawrence M. Krauss in seinem Buch Ein Universum aus Nichts sehr schön beschreibt.

Wenn man nun das bisher gezeigte Bild unseres Universums eine Weile auf sich wirken lässt, so ergeben sich daraus eine Reihe von Fragen:

• Warum ist das Universum eigentlich genau so, wie wir es dargestellt haben?
• Warum ist seine Raumkrümmung gleich Null?
• Warum hat die kosmische Hintergrundstrahlung überall fast genau dieselbe Temperatur von 2,7 Kelvin?
• Wo kommen Raum und Materie ursprünglich eigentlich her – was also zündete den Urknall?

Tatsächlich ist beispielsweise die verschwindende Raumkrümmung keineswegs selbstverständlich. Im Gegenteil: Die sich abschwächende Expansion in den ersten 8 Milliarden Jahren seiner Geschichte müsste nach den Berechnungen auch geringe Raumkrümmungen enorm verstärkt haben, sodass wir eigentlich heute ein gekrümmtes Universum erwarten würden.

Auch die ziemlich gleichmäßige Temperatur der Hintergrundstrahlung ist erklärungsbedürftig: Physikalische Einflüsse konnten sich bis zur Entstehung dieser Strahlung 380000 Jahre nach dem Urknall nur so weit ausgebreitet haben, wie es die großen Temperaturflecken heute anzeigen. Es konnte demnach keinerlei Temperaturausgleich zwischen weiter voneinander entfernten Bereichen des Plasmas seit dem Urknall stattgefunden haben.

Unser bisheriges Bild vom Universum kann diese Fragen nicht beantworten, denn es ist unvollständig. Es macht keine vernünftigen Aussagen darüber, was im Urknall selbst passiert ist, und wir können ihm nicht trauen, wenn es um die allerersten Sekundenbruchteile geht, in denen oben in der Grafik der Skalenfaktor a bis auf Null zurückgeht. Ein Skalenfaktor von Null macht nämlich wenig Sinn – soll er etwa bedeuten, dass es keine Abstände und keinen Raum mehr gibt?

Es gibt ein recht einfaches Modell, das tatsächlich in der Lage ist, die oben angesprochenen Fragen zu beantworten, und das mittlerweile zum Standardmodell für die ersten Sekundenbruchteile des Universums geworden ist: die inflationäre Expansion. Nach dieser Idee entstand unser Universum aus einem mikroskopisch kleinen Raumbereich, der von einem sehr starken Energiefeld durchdrungen war, dem man den Namen Inflatonfeld gegeben hat. Dieses Feld wirkte wie eine sehr starke Raumenergie, die mit ihrem negativen Druck eine extrem abstoßende Gravitation zur Folge hatte. Nach gängigen Rechnungen wäre diese abstoßende Gravitation in der Lage gewesen, innerhalb von nur 10⁻³³ Sekunden den Raumbereich um das 10³⁰ bis 10⁵⁰-fache explosionsartig auszudehnen und somit das hervorzurufen, was wir normalerweise als Urknall bezeichnen. Anschließend zerfällt das metastabile Inflatonfeld in die Materie, die unser Universum seitdem durchdringt.

Diese ersten 10⁻³³ Sekunden mit inflationärer Expansion sind in unserem obigen Bild nicht dargestellt. Nimmt man sie mit hinzu, so ergibt sich für des Radius des expandierenden Raumbereichs, der heute unser sichtbares Universum darstellt, das folgende Bild:

Wie genau dieses mysteriöse Inflatofeld ausgesehen haben könnte, wissen wir heute noch nicht. Solche Felder treten jedoch in vielen noch spekulativen Modellen der Teilchenphysik in natürlicher Weise auf – ganz ähnlich wie das berühmte Higgsfeld, dessen zugehöriges Teilchen (das Higgs-Teilchen) im Jahr 2012 am Large Hadron Collider LHC nachgewiesen werden konnte.

Was die Idee der inflationären Expansion so überzeugend macht, sind ihre Konsequenzen für unser heutiges Universum:

• Die Rechnungen zeigen, dass sich bei der inflationären Expansion automatisch ein sichtbares Universum ergibt, das mit hoher Genauigkeit flach ist – so wie ein extrem aufgeblähter Luftballon flach aussieht, wenn man nur ein winziges Stück seiner Oberfläche sehen kann. Und unser sichtbares Universum wäre aufgrund des enormen Expansionsfaktors eben nur ein solcher winziger Ausschnitt des extrem aufgeblähten Gesamtraums. Es wäre sogar so flach, dass die anschließende abgebremste Expansion es nicht schafft, das sichtbare Universum wieder nennenswert zu krümmen. Daher ist es auch heute noch im Rahmen unserer Messgenauigkeit flach und weist die kritische Dichte auf.

• Vor der inflationären Expansion haben alle Bereiche des heute sichtbaren Universums Kontakt zueinander, sodass es zu einem Ausgleich kommt. Erst die inflationäre Expansion reißt diesen Bereich auseinander und zerlegt ihn in viele Teilbereiche, die anschließend keinen erneuten Kontakt mehr zueinander gehabt haben können. Da der Ausgleich aber schon vorher stattfand, kann die kosmische Hintergrundstrahlung überall nahezu dieselbe Temperatur aufweisen.

• Das Inflatonfeld weist geringe mikroskopische Quanten-Fluktuationen auf, die durch die inflationäre Expansion enorm aufgebläht werden und letztlich zu den Temperaturflecken in der kosmischen Hintergrundstrahlung führen. Dabei zeigen die Berechnungen, dass genau die richtige Fleckenmischung mit den richtigen statistischen Eigenschaften entsteht, so wie wir sie heute beobachten.

Außerdem stellt die inflationäre Expansion einen Mechanismus für den Urknall zur Verfügung und erklärt, wie Raum und Materie unseres Universums aus Nichts oder fast Nichts entstanden sein könnten. Alles, was man zu Beginn braucht, ist ein mikroskopischer Raumbereich, in dem sich aus irgendwelchen Gründen ein starkes Inflatonfeld ausbildet. Im letzten Kapitel haben wir gesehen, wie mithilfe der Quantenmechanik ein solcher Raumbereich gleichsam aus dem Nichts in die Existenz hervorgetunnelt sein könnte. Ist er erst einmal da, so beginnt er rasend schnell zu expandieren, bis das Inflatonfeld zerfällt. Dabei erzeugt die abstoßende Gravitation die Energie, die zur Aufrechterhaltung des Inflationfeldes im expandierenden Raum notwendig ist. Positive Inflatonenergie und negative Gravitationsenergie heben sich dabei zu jeder Zeit gegenseitig auf, d.h. die Gesamtenergie des Universums ist Null. Das bleibt auch nach der Umwandlung des Inflatonfeldes in andere Materie so, sodass auch heute noch die Gesamtenergie des Universums Null ist. Das Universum benötigt für seiner Entstehung also keine oder fast keine Energie!

Interessant ist, dass in der inflationären Expansion Raum und Materie immer zusammen entstehen. Der Raum entsteht nämlich erst durch die Expansion, die durch die abstoßende Gravitation des Inflatonfeldes vorangetrieben wird. Ohne Inflatonfeld gibt es keine Expansion und damit kein makroskopisches Universum. Das Inflatonfeld ist jedoch lediglich eine spezielle Materieform, und es wandelt sich schließlich in die Materie um, die wir heute im Universum vorfinden. Leerer Raum ohne Materie kann zumindest nach diesem Mechanismus nicht entstehen. Gottfried Wilhelm Leibniz und Ernst Mach wären wohl sehr glücklich darüber gewesen – standen sie doch der Idee eines absolut leeren Raums von Anfang an kritisch gegenüber.

Nach dem Modell der inflationären Expansion ist unser sichtbares Universum nur ein winziger Ausschnitt des gesamten Raumes, der bei der extremen inflationären Raumausdehnung entsteht. Wie aber sieht dieser Raum insgesamt aus? Und was geschieht jenseits seiner Grenzen?

Auf diese Fragen können wir heute noch keine endgültigen Antworten geben – ist doch selbst die Idee der inflationären Expansion noch recht spekulativ. Es hängt von den konkreten Annahmen ab, was sich im Modell der inflationären Expansion für ein Universum insgesamt ergibt. Eines jedoch erscheint sicher: Es muss wesentlich größer als der Teil sein, der uns als sichtbares Universum zugänglich ist, sodass der Begriff Multiversum dafür geprägt wurde.

Eine recht verbreitete Idee ist die folgende, die auch als ewige Inflation bezeichnet wird: In einem inflationär expandierenden Raumbereich zerfällt das Inflatonfeld vermutlich nicht überall zugleich zu normaler Materie, sondern der Zerfall erfolgt nur zufällig lokal an einigen Stellen des rapide expandierenden Raums. Dabei kommt es zu einem Wettstreit zwischen der exponentiell anwachsenden Raumausdehnung mit sich ständig nachbildendem Inflatonfeld und dessen zufälligem lokalen Zerfall. Viele Gründe sprechen dafür, dass die Raumausdehnung diesen Wettstreit gewinnt, sodass die inflationäre Expansion ewig weitergeht. An den Stellen, wo das Inflatonfeld zufällig zerfällt, bilden sich dabei ständig neue Raumblasen ohne Inflatonfeld, die sich von der inflationären Expansion abkoppeln. Das Bild erinnert an einen sich schnell aufblähenden Schweizer Käse, dessen Käsemasse das Inflatonfeld darstellt, während die sich ständig neu bildenden Löcher oder Blasen darin den normal expandierenden Raum ohne Inflatonfeld repräsentieren. Unser sichtbares Universum wäre dabei nur ein winziger Teil in einer solchen gigantischen Raumblase.

Am Rand einer solchen Blase zerfällt das Inflatonfeld ständig weiter, sodass sich die Blase nach außen gleichsam in die Käsemasse hineinfrisst. Andere Blasenränder werden dabei aber nicht erreicht, denn der Raum zwischen den Blasen (also die Käsemasse) expandiert dank dem Inflatonfeld ja ständig weiter. Dies ist zumindest das Bild, das sich aus einer äußeren Vogelperspektive ergibt.

Aus der Froschperspektive im Inneren einer Raumblase sieht die Situation dagegen ganz anders aus. Der Zerfall des Inflatonfeldes an den Blasenrändern definiert nämlich den zeitlichen Nullpunkt für die zugehörigen Raumpunkte innerhalb der Blase. Schaut man sich die so entstehenden Flächen der Gleichzeitigkeit innerhalb der Blasen-Raumzeit an, so stellt man fest, dass sie unendlich groß sind, da die Blase von außen gesehen ja unendlich lange anwächst. Obwohl also die Blase von außen betrachtet endlich erscheint, erscheint sie von innen betrachtet unendlich groß – wobei allerdings nur ein winziger Teil von ihr für einen inneren Beobachter wirklich "sichtbar" wäre. Sollte dieses Szenario wirklich zutreffen, so wäre seine Antwort auf die Frage nach der Unendlichkeit des Universums wahrhaftig bizarr!

Die Zahl der Raumdimensionen

Für uns Menschen ist es vollkommen selbstverständlich: Der uns umgebende Raum ist dreidimensional, d.h. wir können an jedem Punkt drei senkrecht aufeinander stehende Richtungen unterscheiden: rechts-links, vorne-hinten sowie oben-unten.

Doch warum ist das so? Mathematisch gibt es nicht den geringsten Grund dafür, dass unser Raum dreidimensional sein muss – er könnte genauso gut 2-dimensional, 4-dimensional oder auch 42-dimensional sein.

Wenn es also keinen mathematischen Grund zu geben scheint, erzwingt dann vielleicht die Physik einen dreidimensionalen Raum? Bei den heute etablierten und experimentell verifizierten physikalischen Theorien wie beispielsweise dem Standardmodell der Teilchenphysik ist das nicht der Fall: Sie funktionieren im Prinzip auch mit einer anderen Dimensionszahl. Mir fällt nur eine einzige physikalische Theorie ein, die zu der Zahl der Raumdimensionen eine eindeutige Aussage macht: die Stringtheorie.

Diese Stringtheorie ist eine noch spekulative Theorie, der es weitgehend gelingt, Quantentheorie und Einsteins Allgemeine Relativitätstheorie der Gravitation unter einem Dach zu vereinen – dies schaffen die heute etablierten Theorien wie das Standardmodell der Teilchenphysik nicht. Während das Standardmodell elementare Teilchen als punktförmige Objekte betrachtet, geht die Stringtheorie von winzigen kleinen Energiefäden als fundamentale Objekte der Welt aus. Die zugehörige String-Quantentheorie ist jedoch nur dann sinnvoll, wenn der Raum zehn Raumdimensionen besitzt (wir betrachten hier die nicht-störungstheoretische Erweiterung der Stringtheorie: die sogenannte M-Theorie, die eine Raumdimension mehr aufweist als die ursprünglichen störungstheoretischen Stringtheorien, die neun Raumdimensionen benötigen).

Der Grund dafür ist mathematischer Natur – eine einfache anschauliche Erklärung scheint es hier nicht zu geben, wie beispielsweise Brian Greene in seinem Buch Die verborgene Wirklichkeit: Paralleluniversen und die Gesetze des Kosmos schreibt. Hier ist also die mathematische Kurzerklärung: In der Stringtheorie gibt es gewisse mathematische Problemterme, die zu unsinnigen Ergebnissen für physikalische Prozesse führen. Diese Problemterme (auch Quanten-Anomalien genannt) verschwinden nur dann, wenn der Raum zehn Dimensionen besitzt, denn die Problemterme treten in der Form \begin{equation} (D - 10) \times \mathrm{Problemterm} \end{equation}

auf, wobei \( D \) die Zahl der Raumdimensionen ist. Für \( D = 10 \) Raumdimensionen ist die Klammer gleich Null und der Problemterm verschwindet.

Blöd nur, dass nicht \( D = 3 \) herauskommt, sondern \( D = 10 \) ! Wie kann die Stringtheorie einen zehndimensionalen Raum vorhersagen, wenn wir doch nur drei Raumdimensionen wahrnehmen? Ist die Stringtheorie damit bereits aus dem Rennen?

Keineswegs, denn entscheidend ist nur, dass wir von den überzähligen Raumdimensionen normalerweise nichts mitbekommen. Sie könnten beispielsweise zu mikroskopisch kleinen Raumknäuel aufgewickelt und in sich verschlungen sein – so klein, dass unsere heute möglichen Experimente sie nicht auflösen und erkennen können. Ein String kann das dagegen schon: Er dringt auch in diese winzigen Raumdimensionen ein und kann in ihnen auf vielfältige Weise zu Schwingungen angeregt werden. Letztlich bestimmt daher die Art und Weise, wie die überzähligen Raumdimensionen im Detail zu den Knäuel aufgewickelt sind, welche Physik wir in den ausgedehnten drei Raumdimensionen wahrnehmen.

Nur warum sollten genau drei der zehn Raumdimensionen ausgedehnt bleiben, sodass für uns der Raum dreidimensional erscheint? Könnten es nicht auch zwei oder vier Raumdimensionen sein? Die Stringtheorie schein diese Möglichkeiten ohne Weiteres zuzulassen, und es ist durchaus denkbar, dass weit außerhalb des für uns sichtbaren Universums andere Raumbereiche existieren, die nicht genau drei ausgedehnte Raumdimensionen besitzen, sondern zwei oder vier oder auch zehn.

Der Grund, der in dem für uns sichtbaren Universum zu drei Raumdimensionen geführt haben könnte, liegt womöglich schlicht in der Tatsache begründet, dass nur in einem Universum mit drei ausgedehnten Raumdimensionen Leben entstehen kann. Das nennt man das anthropische Prinzip. Andere weit entfernte Raumbereiche des Universums mit zwei oder vier Dimensionen könnte es also durchaus geben, nur lebt dort niemand, der sich darüber wundern könnte. In zwei Raumdimensionen würde beispielsweise ein Lebewesen mit einem durchgehenden Darm in zwei Hälften zerfallen – ein solcher Darm wäre also unmöglich und höheres Leben erscheint nur schwer vorstellbar. In vier oder mehr Raumdimensionen würde dagegen die Schwerkraft zur Sonne hin stärker als quadratisch mit sinkendem Abstand anwachsen, sodass die Planetenbahnen nicht stabil wären – die Erde würde in die Sonne stürzen.

Glaubt man der Stringtheorie und dem anthropischen Prinzip, so gäbe es demnach keinen eindeutigen physikalischen Grund für unseren dreidimensionalen Raum. Er könnte bis zu zehn ausgedehnte Raumdimensionen besitzen, und nur die Voraussetzungen für unsere eigene Existenz führen dazu, dass wir uns in einem Raumbereich mit drei ausgedehnten Raumdimensionen wiederfinden. Die von uns wahrgenommenen drei Raumdimensionen wären dann genauso wenig erstaunlich wie die Tatsache, dass wir auf der lebensfreundlichen Erde und nicht auf dem luftleeren Mond oder der heißen Venus leben.

Moderne Entwicklungen in der theoretischen Physik deuten sogar an, dass der Begriff der Raumdimension weniger eindeutig festgelegt sein könnte, als man normalerweise annimmt. Dies wird beispielsweise deutlich, wenn man sich die Frage stellt, wieviel Information – also physikalische Freiheitsgrade – man maximal in einem bestimmten kugelförmigen Raumvolumen unterbringen kann. Die Antwort glaubt man mittlerweile zu kennen (sie folgt aus der Entropie schwarzer Löcher): Die maximale Information liegt dann vor, wenn die Raumkugel komplett von einem schwarzen Loch ausgefüllt wird, dessen Schwarzschildradius gleich dem Kugelradius ist. Pumpt man mehr Information in irgendeiner materiellen Form in die Kugel hinein, so wächst das schwarze Loch und die Kugel wird größer. Dabei wächst die Informationsmenge, die man in der Kugel unterbringen kann, aber nicht proportional zum Kugelvolumen, sondern proportional zu dessen Oberfläche an! Es hat den Anschein, als sei die Information und mit ihr die entsprechende Physik gar nicht in der Kugel selbst gespeichert, sondern auf deren Oberfläche codiert. Könnte es sein, dass die Physik im Kugelinneren einer gleichwertigen Physik auf der Kugeloberfläche entspricht? Welches ist dann aber die korrekte physikalische Raumdimension – die drei Dimensionen des Kugelinneren oder die zwei Dimensionen der Kugeloberfläche?

Tatsächlich kennt man mittlerweile ein Beispiel für eine physikalische Theorie, bei der die Physik in einem Raumvolumen durch eine gleichwertige Physik auf dem Rand dieses Volumens dargestellt werden kann und umgekehrt (gemeint ist hier die sogenannte AdS/CFT-Korrespondenz, die von Juan Maldacena im Jahr 1997 entdeckt wurde). Es ist ganz ähnlich wie bei einem zweidimensionalen Hologramm, das ein dreidimensionales Objekt sichtbar macht, sodass man hier vom holografischen Prinzip spricht. Die Physik der beiden Theorien ist also vollkommen gleichwertig, aber ihre mathematische Beschreibung ist sehr verschieden und basiert auf Räumen mit unterschiedlicher Dimension. Es ist hier also eine Frage des Geschmacks, welche der beiden gleichwertigen Beschreibungen man bevorzugt und für welche Zahl an Raumdimensionen man sich damit entscheidet. Ein verrücktes Ergebnis, das wieder einmal zeigt, wie sich scheinbar wohlbekannte Begriffe wandeln und aufzulösen beginnen, wenn man ihnen mit dem gesamten Instrumentarium der modernen Physik auf den Grund geht.

Der Quantenraum

Auch wenn wir es nicht genauer ausgeführt haben, so spielt bei den obigen Überlegungen zur Zahl der Raumdimensionen die Quantentheorie eine entscheidende Rolle, denn sie liefert die Basis für das Standardmodell, für die Stringtheorie und auch für das holografische Prinzip. Offenbar scheint sich der Begriff des Raums auf merkwürdige Weise zu verändern, wenn wir die Quantentheorie mit ins Spiel bringen, und wir wollen uns im letzten Abschnitt dieses Kapitels genauer ansehen, in welcher Weise dies geschieht.

Die vielleicht wichtigste Eigenschaft des Raumes besteht darin, dass er Lokalität erlaubt: Zwei physikalische Objekte, die sich an verschiedenen Orten aufhalten, existieren unabhängig voneinander. Sie können sich zwar gegenseitig beeinflussen, aber diese Beeinflussung erfordert den Austausch von physikalischen Wirkungen (z.B. Kraftfeldern), die sich höchstens mit Lichtgeschwindigkeit ausbreiten können. Albert Einstein hat dieses Prinzip in seinem Text QUANTEN-MECHANIK UND WIRKLICHKEIT folgendermaßen auf den Punkt gebracht (siehe z.B. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1746-8361.1948.tb00704.x):

"Fragt man, was unabhängig von der Quanten-Theorie für die physikalische Ideenwelt characteristisch ist, so fällt zunächst folgendes auf: die Begriffe der Physik beziehen sich auf eine reale Aussenwelt, d.h. es sind Ideen von Dingen gesetzt, die eine von den wahrnehmenden Subjekten unabhängige "reale Existenz" beanspruchen (Körper, Felder, etc.), welche Ideen andererseits zu Sinneseindrücken in möglichst sichere Beziehung gebracht sind. Characteristisch für diese physikalischen Dinge ist ferner, dass sie in ein raum-zeitliches Kontinuum eingeordnet gedacht sind. Wesentlich für diese Einordnung der in der Physik eingeführten Dinge erscheint ferner, dass zu einer bestimmten Zeit diese Dinge eine voneinander unabhängige Existenz beanspruchen, soweit diese Dinge "in verschiedenen Teilen des Raumes liegen". Ohne die Annahme einer solchen Unabhängigkeit der Existenz (des "So-Seins") der räumlich distanten Dinge voneinander, die zunächst dem Alltags-Denken entstammt, wäre physikalisches Denken in dem uns geläufigen Sinne nicht möglich. Man sieht ohne solche saubere Sonderung auch nicht, wie physikalische Gesetze formuliert und geprüft werden könnten. Die Feldtheorie hat dieses Prinzip zum Extrem durchgeführt, indem sie die ihr zugrunde gelegten voneinander unabhängig existierenden elementaren Dinge sowie die für sie postulierten Elementargesetze in den unendlich-kleinen Raum-Elementen (vierdimensional) lokalisiert.

Für die relative Unabhängigkeit räumlich distanter Dinge (A und B) ist die Idee characteristisch: äussere Beeinflussung von A hat keinen unmittelbaren Einfluss auf B; dies ist als "Prinzip der Nahewirkung" bekannt, das nur in der Feld-Theorie konsequent angewendet ist. Völlige Aufhebung dieses Grundsatzes würde die Idee von der Existenz (quasi-) abgeschlossener Systeme und damit die Aufstellung empirisch prüfbarer Gesetze in dem uns geläufigen Sinne unmöglich machen."

Besser kann man es kaum ausdrücken, und Einsteins Schlussfolgerungen scheinen unausweichlich zu sein. Wie sollte man Physik betreiben, wenn alles unentwirrbar mit allem zusammenhinge? Wie könnte man ein kontrollierbares Experiment aufbauen, wenn das gesamte Universum einen unmittelbaren und unkontrollierbaren Einfluss auf die Resultate hätte?

Und doch kann man folgendes quantenmechanisches Experiment durchführen, das wir uns im späteren Kapitel über Quantentheorie noch genauer ansehen werden:

Man kann eine Teilchenquelle bauen, die zwei Teilchen in entgegengesetzte Richtungen aussendet. Diese beiden Teilchen verhalten sich nicht unabhängig voneinander: Wenn beispielsweise das eine Teilchen in einem inhomogenen Magnetfeld nach oben abgelenkt wird, so wird das andere Teilchen in einem analogen Magnetfeld nach unten abgelenkt und umgekehrt. Ob ein einzelnes Teilchen nach oben oder unten abgelenkt wird, ist dabei vom Zufall bestimmt. In jedem Fall verhalten sie sich aber entgegengesetzt zueinander.

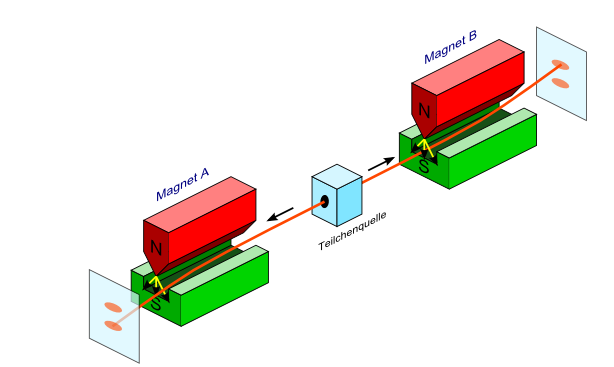
Kein Problem, würde man zunächst denken: Die beiden Teilchen könnten ja Signale miteinander austauschen und so ihr entgegengesetztes Verhalten in dem Moment verabreden, in dem sie beide auf ihr jeweiliges Magnetfeld treffen. Eines der Teilchen entscheidet sich dabei zufällig für eine Ablenkungsrichtung und teilt diese Entscheidung seinem Partnerteilchen mit, das sich dann genau entgegengesetzt verhält. Das Problem ist nur, dass sich beide Teilchen bereits Lichtjahre voneinander entfernt befinden könnten. Da sich Signale höchstens mit Lichtgeschwindigkeit ausbreiten können, wären diese zu langsam, um das entgegengesetzte Verhalten der Teilchen erklären zu können.

Albert Einstein folgerte daraus: Die beiden Teilchen müssen eine innere Eigenschaft wie beispielsweise eine Eigenrotation besitzen, die entgegengesetzt ausgeprägt ist und die zu diesem Verhalten führt. Da die Quantenmechanik solche Eigenschaften nicht beschreibt, müsse sie unvollständig sein. Jedes Teilchen für sich wisse sehr wohl, wie es sich beim Durchgang durch ein Magnetfeld zu verhalten habe, auch wenn uns dieses Wissen vielleicht experimentell nicht zugänglich ist und uns deshalb das Verhalten der Teilchen einzeln wie zufällig erscheint.

Doch viele Jahre nach Einsteins Überlegungen fand man heraus, dass man mit einem trickreichen Experiment die Existenz solcher innerer Teilcheneigenschaften überprüfen kann. Dabei stellte sich heraus: Diese innere Eigenschaft kann es nicht geben (siehe das spätere Kapitel zur Quantentheorie oder mein Buch Die Entdeckung des Unteilbaren).

Damit bleibt uns nur eine Schlussfolgerung: Die beiden Teilchen führen keine voneinader unabhängige Existenz, egal wie weit sie voneinander entfernt sind. Ihr Verhalten ist miteinander verschränkt, und sie müssen als ein gemeinsames physikalisches System betrachtet werden, das sich nicht in zwei voneinander getrennte Bestandteile zerlegen lässt. Einsteins Idee einer lokalen Wirklichkeit hat sich als Illusion erwiesen!

Wie aber ist es dann noch möglich, dass wir überhaupt Physik betreiben können? Die Lösung lautet: Die beiden Teilchen müssen irgendwann einmal sehr nahe beisammen gewesen sein, um sich zu einem gemeinsamen Quantensystem verschränken zu können. In unserem Beispiel oben sind sie sogar zusammen in einer gemeinsam Teilchenquelle entstanden. Daher lassen sich anschließend mit ihnen kontrollierte Experimente durchführen.

Grundsätzlich ist es jedoch so, dass solche verschränkten Quantensysteme sehr empfindlich auf äußere Einflüsse reagieren – sie verschränken sich dann sehr gerne mit der Außenwelt zu einem immer größer werdenden Quantensystem, das experimentell nicht mehr in den Griff zu bekommen ist. Es sieht sogar so aus, also ob wir von dieser Quantenwelt normalerweise nur noch einen winzigen Ausschnitt beobachten können, der unserer eigenen klassischen Realität entspricht, sodass wir nur unter sehr speziellen Bedingungen die Quantennatur dieser Welt beobachten können. Auf diese Weise könnte aus der Quantenwelt die Welt der klassischen Physik entstehen, die uns experimentell zugänglich ist, während wir das große Ganze – also die gesamte Quantenwelt mit ihren unzähligen Verschränkungen quer durch Raum und Zeit – gar nicht wahrnehmen können. Diese universelle Quantenwelt enthält dabei nach der sogenannten Viele-Welten-Interpretation sogar eine gigantische Zahl von sich ständig weiter verzweigenden parallel existierenden klassischen Realitäten, die sich gegenseitig nicht mehr wahrnehmbar beeinflussen, da sich die komplexen Verschränkungen zwischen ihnen zu einem nicht mehr identifizierbaren Rauschen wegmitteln – man nennt das Dekohärenz. In diesem Sinne hat Einstein tatsächlich recht: In einer bizarren global verschränkten Quantenwelt ist keine lokale Physik mehr möglich, die diese Welt noch erfassen könnte. Nur dort, wo diese nichtlokalen Verschränkungen wie in unserem obigen Teilchenexperiment unter kontrollierten Bedingungen lokal entstehen, können wir sie überhaupt noch messen, bevor sie sich schließlich mit dem Rest der Welt verschränken und damit für unsere Messgeräte verloren gehen.

Noch eine weitere scheinbar selbstverständliche Eigenschaft des Raums geht durch die Quantenmechanik verloren: Der leere Raum – das Vakuum – ist gar nicht absolut leer! Man kann ihn sich angefüllt mit einem ständig wabernden und fluktuierenden See aus virtuellen Teilchen und Antiteilchen vorstellen, die spontan entstehen und nach kurzer Zeit wieder verschwinden. Der Grund für dieses Verhalten ist die quantenmechanische Unschärferelation zwischen Energie und Zeit: Für sehr kurze Zeiten kann sich das Vakuum gleichsam Energie borgen und damit Teilchen-Antiteilchen-Paare entstehen lassen, muss aber diese Energieschuld sehr schnell wieder zurückzahlen, sodass die Teilchen-Antiteilchen-Paare dann wieder verschwinden müssen.

Dieser wabernde See ist zwar nicht direkt sichtbar, aber er hat messbare Auswirkungen auf physikalische Prozesse. So sind beispielsweise im Raum zwischen zwei parallelen, eng benachbarten Metallplatten nicht alle Quantenzustände für den fluktuierenden Teilchen-Antiteilchen-See erlaubt, die im Außenraum möglich sind. Dies führt zu einer schwachen Anziehungskraft zwischen den Metallplatten, die tatsächlich experimentell nachgewiesen werden konnte (Casimir-Effekt).

Genau genommen ist das Bild eines wabernden Teilchen-Antiteilchen-Sees im Vakuum stark vereinfacht und entspringt unserem Bedürfnis, sich die Natur in Bildern aus der klassischen Physik vorzustellen. Analog stellt man sich ja oft vor, dass das Elektron in einem Wasserstoffatom den Atomkern umkreist oder in einer Wahrscheinlichkeitswolke wild hin- und herhüpft. Eigentlich bewegt sich in einem Wasserstoffatom aber gar nichts, denn der Betrag der quantenmechanischen Elektronen-Wellenfunktion ist darin statisch wie die maximale Amplitude einer stehenden Welle.

Auch im leeren Raum bewegt sich quantenmechanisch nicht wirklich etwas. Vielmehr ist der leere Raum angefüllt mit einem statischen Vakuum-Quantenzustand, der über den gesamten erreichbaren Raum hochverschränkt – also nichtlokal – ist. Verändert sich in diesem Raum etwas – z.B. indem parallele Leiterplatten im Zwischenraum gewisse Quantenwellen unmöglich machen – so reagiert der Vakuum-Quantenzustand und verändert sich.

Besonders gravierend wird dies, wenn ein Teil des Raumes für einen Beobachter unzugänglich wird, weil es einen Ereignishorizont gibt. So ist bei einem schwarzen Loch für einen außenstehenden Beobachter der Bereich unterhalb des Schwarzschildhorizonts nicht erreichbar – kein Signal kann von dort nach außen dringen. Daher kann es für den Quanten-Vakuumzustand, den der äußere Beobachter wahrnimmt, keine Verschränkungen mit dem Raumbereich unterhalb des Schwarzschildhorizonts geben. Das führt dazu, dass sich der Quanten-Vakuumzustand des äußeren Beobachters verändert: Für ihn geht vom Ereignishorizont des schwarzen Lochs eine sehr schwache Wärme- und Teilchenstrahlung aus – die sogenannte Hawking-Strahlung. Vereinfacht kann man sich vorstellen, dass am Ereignishorizont kurzzeitig Teilchen-Antiteilchen-Paare im Vakuum entstehen, von denen ein Teilchen ins Innere des schwarzen Lochs fällt und dadurch genug Energie bereitstellt, sodass das andere Teilchen nach außen entkommen kann.

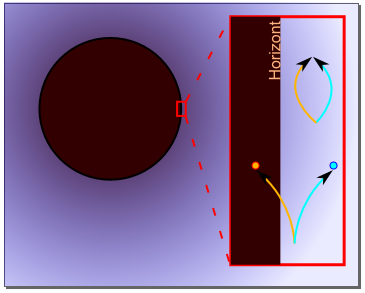
Ein Beobachter, der im freien Fall in das schwarze Loch hineinfällt, nimmt dagegen am Ereignishorizonzt keine solche Hawking-Strahlung wahr, denn er wird auch den Raum innerhalb des Schwarzschild-Radius sehen, sodass sich sein Vakuum-Quantenzustand von dem eines äußeren Beobachters unterscheidet. Das Vakuum und sein Teilcheninhalt hängen damit plötzlich vom Beobachter ab – es gibt also gar keinen objektiv für alle gleichen quantenmechanischen Vakuum-Zustand für den leeren Raum!

Dasselbe gilt auch für Ereignishorizonte, die auf andere Weise entstehen. Sobald für einen Beobachter ein Ereignishorizont existiert, gibt es für ihn auch immer eine sehr schwache Wärmestrahlung im scheinbar leeren Raum, da ein Teil des Raums für ihn unzugänglich wird, sodass sich der globale Quanten-Vakuumzustand für ihn verändert. Ein solcher Ereignishorizont entsteht beispielsweise einfach dadurch, dass sich ein Beobachter gleichmäßig beschleunigt bewegt: Ereignisse, die weit genug hinter ihm stattfinden, wird er niemals sehen können, da er ihrem Signal immer schneller davonläuft, sodass sie ihn nie erreichen können. Also muss ein beschleunigter Beobachter auch eine schwache Wärmestrahlung sehen, die es für ihn nicht mehr gibt, wenn er seine Beschleunigung beendet (Unruh-Effekt).

Ein anderer Ereignishorizont entsteht durch die fortwährend beschleunigte Expansion des Universums für jeden von uns, wie wir oben bei der Raumzeit des Universums gesehen haben. Ereignisse, die heute mehr als 16 Milliarden Lichtjahre von uns entfernt stattfinden, werden wir niemals sehen können, falls unser Universum ewig weiter beschleunigt expandiert. Auch durch diesen Ereignishorizont entsteht eine Wärmestrahlung, die unser Universum durchdringt. Diese Wärmestrahlung ist allerdings unmessbar schwach: Ihre Temperatur dürfte bei nur rund 10⁻³⁰ Kelvin liegen.

Wir sehen, was für eine bizarre Welt die Quantenmechanik entstehen lässt. Für beschleunigte Beobachter enthält der leere Raum eine Wärmestrahlung, für unbeschleunigte Beobachter dagegen nicht – was stimmt denn nun, möchte man ausrufen! Gibt es diese Wärmestrahlung denn nun wirklich? Der Begriff einer objektiv existierenden Realität, wie wir sie kennen, scheint sich zunehmend aufzulösen oder er ist zumindest aus unserer eingeschränkten Froschperspektive heraus nicht mehr wahrnehmbar. Aus einer hypothetischen Vogelperspektive, von der aus man die gesamte Quantenwelt des Universums wahrnehmen kann, mag es eine solche monströse Quantenwirklichkeit vielleicht noch geben, doch niemand, der Teil dieser Quantenwelt ist, wird sie jemals auch nur annähernd in Gänze erfahren können. Für verschiedene Beobachter können unterschiedliche Ausschnitte dieser Quantenwelt zugänglich sein. Einen absolut leeren Raum im Sinne Newtons gibt es dabei nicht, denn auch der Raum ist Teil dieser Quantenwelt mit all ihren Merkwürdigkeiten.

Die Quantenmechanik hält noch weitere Überaschungen für uns bereit: Bisher haben wir den Raum als kontinuierliches Objekt betrachtet, in dem es keine untere Grenze für Abstände gibt: jeder noch so kleine Abstand zwischen zwei Objekten ist erlaubt. Wenn wir die Quantentheorie hinzunehmen, so müssen wir berücksichtigen, dass Materie sich auf mikroskopischer Skala in Form von Wellen ausbreitet. So besitzt ein Elektron in der Hülle eines Atoms keine Flugbahn, sondern um den Atomkern herum schwingt eine stehende Elektronenwelle, deren Schwingungsstärke an jedem Ort angibt, mit welcher Wahrscheinlichkeit man dort ein Elektron antrifft.

Wenn wir nun den momentanen Aufenthaltsort beispielsweise eines Elektrons möglichst genau bestimmen wollen, so müssen wir es mit anderen Teilchen beschießen, die von dem Elektron beeinflusst werden und uns so seinen Aufenthaltsort verraten. Wir könnten beispielsweise das Elektron wie unter einem Mikroskop einer elektromagnetischen Welle (also Photonen) aussetzen, oder wir könnten es auch wie in einem Elektronenmikroskop mit einer Elektronenwelle beschießen. Dabei werden wir umso genauere Ergebnisse erzielen, je kürzer die verwendete Wellenlänge ist.

Eine kürzere Wellenlänge bedeutet aber auch eine höhere Energie der Photonen oder Elektronen in dieser Welle. Hier schlägt nun Einsteins spezielle Relativitätstheorie zu: Irgendwann ist diese Energie nämlich so groß, dass sich beim Beschuss des Elektrons aus dieser Energie neue Elektronen (und ihre Antiteilchen) bilden, die eine weitere Steigerung der Messgenauigkeit verhindern. Der Ort des Elektrons lässt sich daher prinzipiell nur mit einer gewissen Genauigkeit bestimmen.

Wenn wir statt des Elektrons den Ort eines schwereren Teilchens wie beispielsweise eines Myons bestimmen wollen, so sieht die Lage günstiger aus. Man braucht nämlich hier mehr Energie, bis störende Myon-Antimyon-Paare entstehen, sodass man auch eine kürzere Wellenlänge als beim Elektron verwenden kann. Rechnet man diese Überlegung konkret durch, so erhält man als Grenze für die Ortsbestimmung eines Teilchens die sogenannte Comptonwellenlänge, die umgekehrt proportional zur Teilchenmasse ist. Bei einem unendlich schweren Teilchen müsste es also weiterhin prinzipiell möglich sein, dessen Aufenthaltsort mit immer kürzeren Wellenlängen beliebig genau zu bestimmen.

Das ist nun der Moment, in dem Einsteins allgemeine Relativitätstheorie der Gravitation ins Spiel kommt: Nach dieser Theorie hat nämlich jedes punktförmige Teilchen einen sogenannten Schwarzschildradius wie ein schwarzes Loch. Nun ist ein Teilchen nicht wirklich ein schwarzes Loch, aber sein Schwarzschildradius kennzeichnet zumindest den Bereich, unterhalb dem wir die Gravitation nicht mehr weglassen dürfen. Was genau unterhalb dieser Grenze physikalisch geschieht, wissen wir heute noch nicht, aber das Bild eines schwarzen Teilchenlochs legt zumindest Folgendes nahe: Der Schwarzschildradius eines Teilchens verhindert, dass wir den Teilchenort genauer bestimmen können, denn das Teilchen versteckt sich gewissermaßen innerhalb des schwarzen Lochs, das es umgibt.

Comptonwellenlänge und Schwarzschildradius begrenzen also beide zugleich die Genauigkeit bei der Ortsmessung eines Teilchens. Mit wachsender Teilchenmasse schrumpft die Comptonwellenlänge, während der Schwarzschildradius anwächst und bei einer bestimmten Masse gleich der Comptonwellenlänge wird. Das ist die maximal mögliche Ortsauflösung, denn bei weiter wachsender Teilchenmasse verschlechtert sich die Genauigkeit wieder wegen des anwachsenden Schwarzschildradius. Diese maximal mögliche Ortsauflösung trägt den Namen Plancklänge. Sie liegt bei 1,6 · 10⁻²⁰ fm und ist damit um rund zwanzig Zehnerpotenzen kleiner als ein Proton. Zum Vergleich: Würde man ein Proton um zwanzig Zehnerpotenzen vergrößern, so hätte es eine Größe von rund 100 Kilometern. Das macht deutlich, wie unglaublich winzig die Plancklänge ist.

Die Plancklänge liegt weit jenseits unserer heutigen experimentellen Möglichkeiten und wird es vermutlich auch für sehr lange Zeit bleiben. Niemand kann also heute die Physik auf dieser winzigen Längenskala erforschen, sodass uns nichts anderes übrig bleibt, als theoretische Vermutungen über diese Physik anzustellen. Dazu ist es notwendig, Einsteins allgemeine Relativitätstheorie mit der Quantenmechanik zu vereinen, denn beide gehen in die Berechnung der Plancklänge ein, wie wir gesehen haben.

Eine etablierte Theorie, der diese Vereinigung gelingt, gibt es heute noch nicht, aber es gibt verschiedene Ansätze in diese Richtung, insbesondere die Stringtheorie und die Loop-Quantengravitation. In beiden Theorien gibt es eine untere Grenze für physikalisch erfassbare Abstände, die in der Größenordnung der Plancklänge liegt. In der Loop-Quantengravitation erhalten Raum und Zeit dabei sogar eine schaumige Struktur, in der sich die klassische Raumzeit als emergentes Phänomen erst dann ergibt, wenn über viele Bläschen gemittelt werden kann. Die Plancklänge führt dabei über die Lichtgeschwindigkeit auch zu einer unteren Grenze für Zeitintervalle: die Planckzeit – das ist die Zeit, die ein Lichtstrahl braucht, um eine Plancklänge zurückzulegen. Könnte man kürzere Zeitintervalle physikalisch realisieren, dann könnte man mit einem Lichtstrahl, den man für dieses Zeitintervall fliegen lässt, auch kürzere Abstände als die Plancklänge physikalisch darstellen und die Plancklänge wäre nicht mehr die untere Grenze für physikalisch sinnvolle Abstände.

Im Licht der modernen Physik könnte damit der uns so vertraute Raum nichts weiter als eine Illusion zu sein, die sich umso mehr auflöst, je tiefer wir in ihre innere Struktur vordringen. So wie die Zeit ist auch der Raum vermutlich kein fundamentales Konzept, sondern er entsteht als klassische Näherung in einer Welt, die letztlich von der Quantenmechanik bestimmt wird. Die wahre Realität des Raumes – wenn es sie denn überhaupt gibt – scheint dabei im Inneren einer kaum begreifbaren global verschränkten Quantenwelt verborgen zu liegen, und es ist heute noch völlig offen, ob es uns als Teil dieser Quantenwelt überhaupt gelingen kann, ihre wahre Natur jemals zu begreifen.

Literatur:

• Brian Greene: Der Stoff, aus dem der Kosmos ist, Siedler Verlag (2004)

• Brian Greene: Die verborgene Wirklichkeit: Paralleluniversen und die Gesetze des Kosmos, Siedler Verlag (2012)

• Claus Kiefer: Der Quantenkosmos: Von der zeitlosen Welt zum expandierenden Universum, S. Fischer Verlag (2009)

• Lawrence M. Krauss: Ein Universum aus Nichts, Knaus Verlag (2013)

• Andreas Müller: Raum und Zeit: Vom Weltall zu den Extradimensionen - von der Sanduhr zum Spinschaum , Spektrum Akademischer Verlag (2013)

• Tamara M. Davis und Charles H. Lineweaver: Expanding Confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe, http://arxiv.org/abs/astro-ph/0310808v2.

• Jörg Resag: Zeitpfad – Die Geschichte unseres Universums und unseres Planeten, Springer Spektrum Verlag (2012)

• Benjamin Bahr, Jörg Resag, Kristin Riebe: Faszinierende Physik: Ein bebilderter Streifzug vom Universum bis in die Welt der Elementarteilchen, Springer Spektrum Verlag (2013)