
Quelle: Wikimedia Commons File:Max Planck (1858-1947).jpg, dort public domain
Photonen: Quanten des Lichts
Materiewellen
Wellenfunktionen, Wahrscheinlichkeitsamplituden und das Rätsel der Messung
Das erste Objekt, das man historisch als ein Quant bezeichnete, dürfte das Photon gewesen sein. Photonen sind Lichtquanten oder allgemeiner: Photonen sind die Quanten der elektromagnetischen Wechselwirkung. Nur – was wollen uns diese Worte sagen?
Max Planck war um das Jahr 1900 der Erste, der auf die Idee der Lichtquanten stieß. Er untersuchte damals die elektromagnetische Wärmestrahlung, wie sie beispielweise im Inneren eines gleichmäßig beheizten Ofens anzutreffen ist. Die in dieser Strahlung vorhandene Energie verteilt sich dabei in charakteristischer Weise auf die einzelnen Wellenlängen, wobei ein Maximum auftritt, das sich bei wachsender Temperatur zu kürzeren Wellenlängen hin verschiebt.
Das kennen wir aus dem Alltag: Ein sich aufheizender Körper sendet zunächst nur unsichtbares Infrarot aus,
aber bei ansteigender Temperatur beginnt er irgendwann, rötlich zu glühen.
Steigern wir die Temperatur weiter, so geht das Glühen schließlich in den gelblichen Wellenlängenbereich
über und kann schließlich sogar bis ins gleißend-bläuliche hinein verschoben werden.
Ein normaler Ofen wird das natürlich nicht aushalten, aber es gibt beispielsweise sehr heiße
Sterne, die im bläulichen Licht strahlen, so wie der gut sichtbare blaue Überriese Rigel
im Sternbild Orion (siehe unten).

Quelle:
Wikimedia Commons File:Max Planck (1858-1947).jpg, dort public domain
Dabei nimmt die insgesamt die Strahlungsenergie mit der vierten Potenz der Temperatur zu, d.h.
heiße Sterne strahlen (bei gleicher Oberfläche) sehr viel mehr Energie ab als kühlere Sterne.
Viele Sterne, die wir am Nachthimmel sehen können, sind daher solche sehr heißen Sterne,
denn obwohl sie seltener als kühlere Sterne sind, können wir ihr helles bläuliches Licht über viel weitere
Entfernungen sehen als das schwache gelblich-rötliche Licht vieler kühlerer Sterne.

Quelle:
Wikimedia Commons File:BlackbodySpectrum lin 150dpi de.png,
Creative Commons Attribution-Share Alike 3.0 Unported license, Author: Sch

Quelle:
Wikimedia Commons File:Bochumer Verein-23-50078.jpg,
Creative Commons Attribution-Share Alike 3.0 Unported license, Author: Rainer Halama

Quelle:
Wikimedia Commons File:Orion Head to Toe - Reduced.jpg,
Autor: Rogelio Bernal Andreo,
Creative Commons Attribution-Share Alike 3.0 Unported license.
Max Planck versuchte nun, diese Energieverteilung aus den damals bekannten Prinzipien
herzuleiten.
Eines dieser Prinzipien ist der Gleichverteilungssatz der Energie:
Jeder Freiheitsgrad besitzt im thermischen Gleichgewicht im zeitlichen Mittel dieselbe Energie,
die dabei proportional zur Temperatur anwächst.
Was sind nun die Freiheitsgrade des elektromagnetischen Feldes in einem Ofen?
Es sind die stehenden Wellen (Schwingungen), die das elektromagnetische Feld im Ofen ausbilden kann,
ähnlich den stehenden Wellen auf einer schwingenden Gitarrensaite.
Es gibt also im Ofen Schwingungen mit einem, zwei, drei und mehr Schwingungsbäuchen
zwischen den Ofenwänden,
und zwar in jeder der drei Raumrichtungen.

Quelle:
Wikimedia Commons File:Waves in Box.svg,
Creative Commons Attribution-Share Alike 3.0 Unported license,
Author: Badseed working on a raster by Brews_ohare
Jede dieser Wellen müsste nach dem Gleichverteilungssatz im Mittel dieselbe Energie aufweisen. Das Problem ist nun aber: Je kürzer die Wellenlänge der Schwingung ist, umso mehr stehende Wellen passen pro Wellenlängenintervall in den Ofen. Es gibt also zu kürzeren Wellenlängen hin eine ständig zunehmde Zahl von möglichen Schwingungen im Ofen, und jede dieser Schwingungen müsste dieselbe Energie aufweisen. In Summe müsste daher die elektromagnetische Strahlung im Ofen eine unendlich große Energie besitzen, was natürlich Unsinn ist – nur wo genau liegt der Fehler?
Das Problem wäre gelöst, wenn zu kurzen Wellenlängen hin irgendwann keine Energie mehr in den elektromagnetischen Schwingungen im Ofeninneren vorhanden wäre, denn dann gäbe es nur endlich viele Schwingungen, die Energie enthielten. Max Planck kam daher nach vielen Versuchen auf die folgende bahnbrechende Idee: Wie wäre es, wenn eine stehende Welle nicht beliebige Energiewerte aufweisen könnte, sondern nur ganzzahlige Vielfache eines gewissen Minimalwertes (Energiequants), der proportional zur Schwingungsfrequenz (und damit umgekehrt proportional zur Wellenlänge) anwächst?
Bei den Schwingungen mit großen Wellenlängen und damit wenigen Schwingungsbäuchen ist das kein Problem: Die Frequenz der Schwingung und damit der Energie-Minimalwert sind niedrig, sodass die mittlere thermische Energie, die ein Freiheitsgrad nach dem Gleichverteilungssatz aufweisen sollte, normalerweise deutlich größer sein wird als der Minimalwert. Diese Schwingungen werden also ein ganzzahliges Vielfaches des zugehörigen Minimalwertes an Energie tragen, sodass sie alle ungefähr dieselbe mittlere thermische Energie aufweisen.
Bei den Schwingungen mit hoher Frequenz und damit vielen Schwingungsbäuchen ist das anders,
sobald der notwendige Minimalwert deutlich größer wird als die mittlere thermische Energie,
welche die Schwingung im Mittel aufweisen sollte.
Diese Schwingung wird dann normalerweise gar keine Energie mehr enthalten,
denn die zur Verfügung stehende thermische Energie reicht meist nicht mehr aus,
um den notwendigen Minimalwert zur Verfügung zu stellen.
Nur ganz selten wird zufällig noch genügend Energie auf die Schwingung entfallen,
um sie kurzzeitig anzuregen. Im Normalfall sind diese Schwingungs-Freiheitsgrade
des elektromagnetischen Feldes also eingefroren, d.h. diese Schwingungen kommen
im Feld nicht vor.

Mit dieser Idee im Gepäck gelang es Max Planck tatsächlich, das Problem mit der unendlichen Energie zu lösen und die Energie-Verteilungskurven für die Strahlung im Ofen exakt zu reproduzieren. Da die Minimal-Energie \( E \) einer Schwingung proportional zu seiner Frequenz \( f \) ansteigen sollte, musste er allerdings einen entsprechenden Proportionalitätsfaktor einführen, den er \( h \) nannte, was lustigerweise damals für hilf stand: \begin{equation} E = h f \end{equation} Heute bezeichnen wir \( h \) als Planck'sches Wirkungsquantum oder auch einfach als Planck-Konstante, was der bescheidene Max Planck selbst natürlich niemals getan hätte. Wie groß \( h \) in der Natur tatsächlich ist, kann man beispielsweise aus der Energie ablesen, die die einzelnen Frequenzbereiche der Wärmestrahlung im Ofen bei einer bestimmten Temperatur enthalten.
Die Energieportionen \( E = h f \), die bei einer bestimmten Frequenz für eine stehende Welle zur Verfügung stehen, werden auch Lichtquanten genannt und man sagt, dass Energie nur in Form dieser Quanten für die einzelnen Schwingungen zur Verfügung steht: Energie ist in diesem Sinne quantisiert. Max Planck hatte sich das damals noch so vorgestellt, dass die Ofenwände eben nur solche Energieportionen an das Strahlungsfeld im Ofeninneren abgeben können.
Albert Einstein ging da im Jahr 1905 weiter, als er versuchte,
eine Erklärung für den Photoeffekt zu finden.
Beim Photoeffekt lässt man Licht einer bestimmten Frequenz
im Vakuum auf eine Alkalimetalloberfläche treffen.
Ab einer bestimmten Minimalfrequenz kann das Licht dabei
einzelne Elektronen aus der Metalloberfläche herausschlagen.
Erhöht man die Lichtfrequenz weiter, so überträgt das Licht
immer mehr Energie auf die Elektronen.
Erhöht man dagegen die Lichtintensiät (Helligkeit)
bei konstanter Frequenz, so erhöht sich die Elektronenenergie nicht, sondern
es werden nur mehr Elektronen herausgeschlagen.

Die klassische Physik des Lichts kann dieses Resultat nicht erklären. Eine erhöhte Lichtintensität führt dort nämlich zu stärkeren elektrischen Feldern, sodass diese die Elektronen umso eher aus dem Metall herauslösen müssten, je intensiver das Licht ist.
Einstein erkannte, was zur Erklärung notwendig war: Die Lichtquanten von Max Planck waren mehr als nur abstrakte Energiepakete, die von der Wand an die Wärmestrahlung abgegeben werden konnten. Die Strahlung selbst bestand aus solchen umherfliegenden lokalisierten Energiepaketen, die man auch als Lichtteilchen interpretieren konnte:
Diese Photonen sind die Energiequanten, auf die Max Planck gestoßen war.
Beim Photoeffekt treffen diese Lichtteilchen nun auf die Elektronen
des Metalls und schlagen sie regelrecht aus dem Metall heraus.
Je höher die Frequenz (und damit je kürzer die Wellenlänge)
des Lichts ist, umso
größer ist nach Planck's Formel \( E = h f \)
die Energie der Photonen und damit die Energie der herausgeschlagenen
Elektronen.
Je intensiver das Licht ist, umso mehr Photonen sind darin enthalten.

Wie verträgt sich die Idee der Lichtteilchen mit der Beschreibung von Licht als elektromagnetische Welle, mit der man so viele Phänomene erfolgreich beschreiben kann?
Nun, offenbar ist auch die elektromagnetische Welle nur eine angenäherte Beschreibung von Licht, so wie die Beschreibung durch Lichtstrahlen nur eine Näherung für kurze Wellenlängen und große Dimensionen ist. Wenn viele Photonen kohärent (also in gleicher Weise) zu einem physikalischen Prozess beitragen, sodass einzelne Photonen nicht ins Gewicht fallen, dann lässt sich der Prozess auch gut näherungsweise mithilfe einer elektromagnetischen Welle beschreiben. Sind es jedoch – wie beim Photoeffekt – nur einzelne Photonen, die einen physikalischen Effekt auslösen, dann ist eine elektromagnetischen Welle als Beschreibung nicht ausreichend.
Photonen sind jedoch keine klassischen Teilchen mit Teilchenbahnen. Ihre Ausbreitung muss durch eine Wahrscheinlichkeitswelle beschrieben werden, deren Intensität (also deren quadrierte Maximalamplitude) in einem Raumvolumen die Wahrscheinlichkeit dafür angibt, Photonen dort anzutreffen. Bei sehr vielen Photonen geht diese Wahrscheinlichkeitswelle dabei in die elektromagnetische Welle über, die wir kennen.
Wow – das ist schon ungewohnt. Plötzlich taucht hier der Begriff der Wahrscheinlichkeit auf, und es sieht heute ganz so aus, als sei der Zufall in der Quantentheorie grundsätzlicher Art. Das Photon weiß gewissermaßen selbst nicht, wo es ist, bis es durch eine Wechselwirkung (z.B. dem Auftreffen auf einem empfindlichen Detektor) zu einer Entscheidung gezwungen wird. Mehr dazu später sowie im Kapitel Was ist Realität?.
Der Wellenbegriff – also die Wahrscheinlichkeitswelle – ist das neue fundamentale Werkzeug in der Quantentheorie, das den Begriff der Teilchenbahn ersetzt. Damit das Sinn macht, müssen Teilcheneigenschaften wie Energie \( E \) und Impuls \( p \) irgendwie mit Welleneigenschaften wie Frequenz \( f \) und Wellenlänge \( \lambda \) zusammenhängen. Für die Energie kennen wir den Zusammenhang bereits: die Photonenergie wächst proportional mit der Wellenfrequenz, und der Übersetzungsfaktor ist das Planck'sche Wirkungsquantum \( h \), also \( E = h f \).
Das kann man noch etwas anders schreiben, wenn man bedenkt, dass die Frequenz \( f \) gerade gleich dem Kehrwert der Schwingungsperiode \( T \) ist, also der Zeit, die an einem Ort vergeht, bis die Welle dort einmal hin- und zurückgeschwungen ist: \( f = 1/T \). Insgesamt haben wir also \( E = h f = h/T \). Ganz analog zu Energie \( E \) und Schwingungsperiode \( T \) hängen nun auch Impuls \( p \) und Wellenlänge \( \lambda \) zusammen: \( p = h/\lambda \), sodass wir insgesamt haben: \begin{align} E &= h/T = h f \\ p &= h/\lambda \end{align} Das muss auch so sein, denn bei einer Welle ist die Wellengeschwindigkeit (also bei Licht die Lichtgeschwindigkeit \( c \) ) gerade gleich der Wellenlänge \( \lambda \) dividiert durch die Zeit für den Durchgang einer Wellenlänge, also die Schwingungsperiode \( T \). Also gilt \( c = \lambda / T \) oder umgestellt \( c / \lambda = 1 / T = f \). Multipliziert man das mit dem Planck'schen Wirkungsquantum \( h \), also \( c h / \lambda = h f \) und verwendet dann die obigen Formeln für Energie und Impuls, so erhalten wir \( c p = E \), also die richtige Beziehung zwischen Energie und Impuls masseloser Teilchen, zu denen das Photon gehört. Alles passt damit wunderbar zusammen.
Für Licht gibt es also einen engen Zusammenhang zwischen Wellen und Teilchen (Photonen), wobei die Wellen letztlich Wahrscheinlichkeitswellen sind. Dies hatten die Arbeiten von Max Planck zur Wärmestrahlung um das Jahr 1900 und von Albert Einstein zum Photoeffekt im Jahr 1905 belegt. War Licht damit etwas Besonderes? Oder galt dieser Zusammenhang zwischen Wellen und Teilchen womöglich ganz allgemein für die gesamte Materie, also beispielsweise auch für das Elektron, und zwar mit genau denselben Formeln zwischen Wellen- und Teilchengrößen wie beim Licht oben?
Diese gewagte Hypothese äußerte Louis de Broglie im Jahr 1924 in seiner Doktorarbeit
und schockierte damit viele seiner Zeitgenossen.
Bald jedoch wurde klar, dass er Recht hatte, denn man konnte in den Jahren 1927 und 1928
mithilfe von Interferenz- und Beugungsexperimenten demonstrieren, dass es Elektronenwellen gab.
Am eindrucksvollsten sieht man das im Doppelspaltexperiment, bei dem
eine Welle durch zwei kleine Spalte durchtritt, sodass sich hinter den Spalten zwei Kugelwellen
bilden und überlagern. In bestimmten Richtungen verstärken sich diese dabei, in anderen Richtungen
löschen sie sich dagegen gegenseitig aus.
Stellt man hinter dem Doppelspalt in einiger Entfernung einen Detektorschirm auf,
so treffen wie zufällig nach und nach immer mehr Elektronen
dort ein. Im Lauf der Zeit wird dabei ein Streifenmuster sichtbar:
Dort, wo die beiden Kugelwellen sich verstärken, treffen auch viele Elektronen ein,
während dort, wo sie sich auslöschen, wenige bis gar keine Elektronen auftreten.
Die Intensität der Welle gibt also die Wahrscheinlichkeit für das Auftreten der
Elektronen an, ganz im Sinne der oben diskutierten Wahrscheinlichkeitswelle.

Quelle:
Wikimedia Commons File:Broglie Big.jpg, dort public domain.

Quelle:
Wikimedia Commons File:Doubleslit3Dspectrum.gif,
Autor: Lookang many thanks to Fu-Kwun Hwang and author of Easy Java Simulation = Francisco Esquembre
Creative Commons Attribution-Share Alike 3.0 Unported license.

Quelle:
Wikimedia Commons File:Double-slit experiment results Tanamura 2.jpg,
dort veröffentlicht unter der
Creative Commons Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Unported
Lizenz.
Mit der Erkenntnis von Louis de Broglie begann die rasante Entwicklung der Quantentheorie
durch Werner Heisenberg, Erwin Schrödinger und viele andere junge Physiker.
So gelang es Erwin Schrödinger im Jahr 1926, seine berühmte Wellengleichung
(Schrödingergleichung) für nichtrelativistische Materiewellen aufzustellen.
Mit dieser Gleichung ließen sich die Elektronenhüllen der Atome verstehen:
Dort bildeten sich stehende Elektronenwellen aus, die mit ihren unterschiedlichen
Schwingungsmöglichkeiten die verschiedenen Elektronenschalen erklärten.
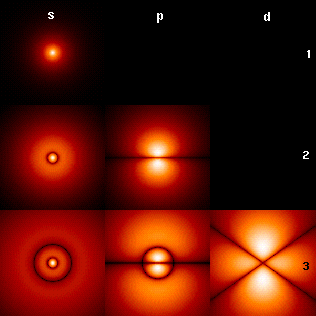
Quelle:
Wikimedia Commons File:HAtomOrbitals.png, von Florian Marquardt,
Creative-Commons
-Lizenz
Namensnennung - Weitergabe unter gleichen Bedingungen 3.0 nicht portiert
Später gelang es Paul Dirac, Richard Feynman und anderen, die Quantenmechanik auch auf relativistische Teilchen und Felder zu verallgemeinern. Nicht nur Wellen, sondern auch statische Kraftfelder erhalten dabei einen engen Zusammenhang zu Teilchen – so werden nicht nur Lichtwellen, sondern auch allgemeine elektromagnetische Felder durch Photonen beschrieben.
Dabei treten überaschende Nebeneffekte zu Tage. So stellt es sich heraus, dass Teilchen einen quantisierten Eigendrehimpuls besitzen können, der ein halbzahliges oder ganzzahliges Vielfaches des reduzierten Planck'schen Wirkungsquantums \( \hbar = \frac{h}{2 \pi} \) beträgt. Materieteilchen wie Protonen, Neutronen oder Elektronen tragen dabei Spin 1/2 (mal \(\hbar\) ), während Feldteilchen wie das Photon Spin 1 tragen (das Graviton trägt sogar Spin 2). Das hat weitreichende Konsequenzen, denn Teilchen mit halbzahligem Spin (sogenannte Fermionen) verhalten sich ganz anders als Teilchen mit ganzzahligem Spin (sogenannte Bosonen). Kurz gesagt: Fermionen meiden sich (können nicht im selben Quantenzustand vorliegen), während Bosonen sich geradezu lieben. Das ist der Grund dafür, warum Elektronen als Fermionen alle Quantenzustände (Schalen) in einer Atomhülle nach und nach auffüllen, während sich Bosonen alle in der niedrigsten Schale versammeln würden. Dieses sogenannte Pauli-Prinzip kann man anschaulich nur schwer erklären; seine Ursache ist mathematischer Natur und liegt tief in der Vereinigung von Relativitätstheorie und Quantenmechanik begründet.
Ein anderer überaschender Effekt war das Auftreten negativer Energien. Es dauerte etwas, bis man erkannte, wie man dieses zunächst rein mathematische Artefakt physikalisch angemessen interpretieren musste: als die Existenz von Antiteilchen. Paul Dirac sagte diese Antiteilchen im Jahr 1928 aufgrund seiner mathematischen Analyse voraus, und schon vier Jahre später (also 1932) entdeckte man das Antiteilchen des Elektrons – das Positron – in der kosmischen Höhenstrahlung.
Besonders merkwürdig wird es, wenn man sich den leeren Raum, also das Vakuum, im Licht der relativistischen Quantentheorie ansieht. Es entpuppt sich als ein komplexes globales Quantengebilde, das man sich oft als wabernden und fluktuierenden See aus kurzzeitig entstehenden und wieder vergehenden virtuellen Teilchen vorstellt.
Das alles zeigt, dass die Quantenmechanik weit über den einfachen Zusammenhang zwischen Wellen und Teilchen hinausgeht, den wir oben kennengelernt haben. Schauen wir uns das nun etwas genauer an.
Das Wellenbild, das wir oben kennengelernt haben, passt gut, wenn wir die Ausbreitung einer ebenen Lichtwelle oder einer Elektronenwelle betrachten und uns die Frage stellen: Wie hoch ist die Wahrscheinlichkeit dafür, an irgendeiner Stelle ein Photon oder Elektron zu finden? Photonen sind dann die Quanten des Lichts, und Elektronen die Quanten der Elektronenwelle.
Doch schon bei etwas komplizierteren Systemen passt dieses einfache Wellenbild nur noch eingeschränkt. Ein Beispiel dafür sind die beiden Elektronen in der Hülle eines Heliumatoms. In einführenden Chemievorlesungen bekommt man hier zunächst folgendes Bild vermittelt:
Die Elektronen bilden im Heliumatom ganz analog zum Wasserstoffatom stehende Wellen (Orbitale genannt) aus, wobei sich jedes Elektron unabhänig vom anderen Elektron in einer dieser stehenden Wellen befinden kann. Sind sie in derselben Welle – beispielsweise im Grundzustand – so müssen sie entgegengesetzten Spin aufweisen (Pauli-Prinzip).
Dieses vereinfachte Bild vernachlässigt jedoch die Wechselwirkung zwischen den beiden Elektronen. Das präzise Bild sieht dagegen so aus:
Man stellt zunächst die gleichzeitig messbaren Daten der beiden Elektronen zusammen, also hier die beiden Orte \( \boldsymbol{x}_1 \) und \( \boldsymbol{x}_2 \) der Elektronen, die kontinuierlich viele Werte annehmen können, sowie die beiden Elektronenspins \( s_1 \) und \( s_2 \), die jeweils nur die beiden Werte +1/2 und −1/2 (mal \(\hbar\)) aufweisen können. Die Menge aller möglichen Messwerte nennt man den sogenannten Konfigurationsraum des Systems. Die Wellenfunktion \( \psi \) der beiden Elektronen ordnet nun jedem Punkt des Konfigurationsraums – also jeder Kombination aus zwei Elektronenorten und zwei Elektronenspins – eine komplexe Zahl \( \psi ( \boldsymbol{x}_1, \boldsymbol{x}_2, s_1, s_2 ) \) zu, die man auch Wahrscheinlichkeitsamplitude nennt. Man kann sich diese Wahrscheinlichkeitsamplitude als Pfeil oder Uhrzeiger in einer zweidimensionalen Ebene vorstellen. Das Längenquadrat dieses Pfeils ist nun die Wahrscheinlichkeit dafür, die entsprechende Messwertkombination im Experiment zu finden.
Das entscheidende ist nun, dass dadurch die beiden Elektronen zu einem einzigen Quantensystem verschmelzen, das sich nicht mehr in zwei Einzelelektronen aufteilen lässt. Nur Fragen, die beide Elektronen gemeinsam betreffen, lassen sich klar beantworten. Das Ganze ist mehr als die Summe seiner Teile! Statt von einzelnen Quanten (Elektronen) müssen wir also letztlich vom gesamten Quantensystem sprechen.
In einem Festkörper mit einer makroskopischen Anzahl an Atomen (sagen wir, 1020 ) ergibt sich so ein gigantischer Konfigurationsraum mit einer unglaublich komplexen Wellenfunktion, die kein Computer jemals exakt berechnen kann. Die Quantenwelt versinkt im Chaos der Möglichkeiten, und man fragt sich, wie aus diesem Chaos unsere klassische Welt entstehen kann, in der ein Festkörper ein so klar definiertes und greifbares Objekt zu sein scheint. Anders gefragt: Wie konkretisieren sich die Messwerte, die in dem Meer aus Quanten-Wahrscheinlichkeiten angeboten werden? Was zwingt ein Elektron zur Entscheidung, sich an einem bestimmten Ort zu zeigen?
Vieles ist hier noch rätselhaft und nicht wirklich verstanden. Keiner weiß genau, wie aus der Quantenmöglichkeit die klassische Gewissheit wird. Manche sagen, dieses Rätsel sei unlösbar: Quantenwelt und klassische Welt seien grundverschieden, und die Quantenwelt besitze keine wirkliche Realität, sondern lebe nur in Wahrscheinlichkeiten, die in der Wellenfunktion zum Ausdruck kommen und die sich dann durch Messwerte in der klassischen Welt zeigen.
Das Problem bei dieser Sichtweise ist nur: Es scheint keine prinzipielle Grenze für die Quantenwelt zu geben, und vieles spricht dafür, dass sie letztlich auch unsere makroskopische Welt bestimmen sollte. Die Trennung zwischen klassischer Welt und Quantenwelt ist also künstlich und muss überwunden werden.
Eine Idee erscheint mir persönlich dabei besonders attraktiv – sie entstammt der sogenannten Viele-Welten-Interpretation. Demnach wird unser gesamtes Universum grundsätzlich durch eine Wellenfunktion in einem fast unermesslich großen Konfigurationsraum beschrieben. Das gesamte Universum ist damit ein einziges verbundenes Quantensystem, in dem alle Teile miteinander zusammenhängen.
Ein allwissendes Wesen könnte nun gleichsam aus der Vogelperspektive diese Wellenfunktion analysieren und Rückschlüsse über das Universum daraus ziehen. Wir selbst sind jedoch ein lokalisierter Teil dieser Wellenfunktion und können daher aus unserer Froschperspektive heraus niemals all die nichtlokalen Informationen ermitteln, die in dieser Wellenfunktion stecken. Der weitaus größte Teil des Quantenuniversums ist für uns unzugänglich.
Die für uns sichtbare klassische Realität entsteht durch ständige Abtrennung (Dekohärenz) einzelner Zweige in dieser Wellenfunktion, die den für uns lokal erfassbaren Messwerten über das Universum entsprechen – beispielsweise den verschiedenen Werten für den Elektronenort. Dabei scheinen die Zweige aus unserer Froschperspektive heraus unabhängig voneinander zu sein scheinen, sodass wir immer nur einen bestimmten Zweig mit zugehörigem klassischen Messwert sehen. Wir selbst sind dabei Teil eines solchen Zweiges, und beim Aufteilen in neue Teilzweige (entsprechend den einzelnen möglichen Messwerten) entstehen auch immer Kopien von uns selbst, wobei jede Kopie sich für einzigartig hält und jeweils einen anderen Messwert sieht und diesen dann als "zufällig" empfindet. Das Quantenuniversum beinhaltet also einen sich ständig weiter verzweigenden Baum aus klassischen Realitätszweigen, die voneinander unabhängigen klassischen Welten entsprechen.
Das ist zugegebenermaßen alles ziemlich abstrus, aber physikalisch durchaus eine logische Konsequenz, wenn man die Quantenmechanik bis in den klassischen Bereich hinein ausweitet. Wir werden uns das noch genauer im Kapitel Was ist Realität ansehen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 13 February 2023