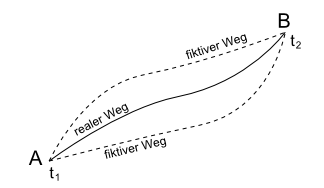
Reale und fiktive Bewegungen eines Körpers zwischen den Punkten A und B.
Zusammenfassung des Buchkapitels:
Wie sich Körper bewegen: Newtons Gesetze der Mechanik
Wie bewegt sich eine Kanonenkugel, ein Pfeil oder ein Planet? Gelten im Himmel dieselben Bewegungsgesetze wie auf der Erde? Diese Fragen wurden bis in die frühe Neuzeit hinein intensiv diskutiert.
Oft ging man dabei davon aus, dass ein Objekt anhält, sobald kein äußerer Einfluss mehr auf es einwirkt. Das entspricht zwar unserer Erfahrung, doch es ist falsch. Richtig ist das folgende Gesetz:
Dieses Trägheitsgesetz wurde zuerst von Galileo Galilei im Jahr 1638 formuliert. Im Jahr 1687 – also knapp 50 Jahre später – übernahm Isaac Newton dieses Gesetz als erstes Bewegungsgesetz in sein revolutionäres Werk Philosophiae Naturalis Principia Mathematica, mit dem er die modernen Grundlagen der Mechanik schuf. Seitdem nennt man es allgemein erstes Newtonsches Gesetz (oder Axiom).
Um die Änderung der Geschwindigkeit (also die Beschleunigung) angeben zu können, prägte Newton den Begriff der Kraft, die den äußeren Einfluss auf den Bewegungszustand eines Körpers repräsentiert. In seinem zweiten Bewegungsgesetz sagt er:
Heute schreiben wir Newtons zweites Bewegungsgesetz meist in der Kurzform
oder als Formel \[ F = m \, a \] Die Masse \(m\) kommt als Proportionalitätskonstante ins Spiel und gibt an, wie groß die Trägheit des beschleunigten Körpers ist.
Newtons zweites Gesetz ist in dieser Form übrigens nur eine Näherung, die bei Geschwindigkeiten deutlich unterhalb der Lichtgeschwindigkeit gilt, was für Planeten vollkommen ausreicht. Bei größeren Geschwindigkeiten wächst nämlich die Trägheit eines Objekts an, was man durch den sogenannten Lorentz-Faktor \(\gamma\) berücksichtigt, der zur Masse hinzukommt (die Trägheit ist dann gleich \(m \gamma\)).
Das Prinzip der kleinsten Wirkung − ein Grundpfeiler der Physik
Nach Newtons Entdeckung stürzten sich Mathematiker wie Leonhard Euler, Joseph Louis Lagrange und William Rowan Hamilton auf seine Bewegungsgleichung. Dabei stießen sie auf eine Umformulierung des Bewegungsgesetzes, die als Prinzip der kleinsten Wirkung bekannt geworden ist und die Feynman an der Highschool so fasziniert hatte, als sein Physiklehrer Abram Bader sie ihm zeigte.
Wir haben das Prinzip der kleinsten Wirkung bereits kurz kennengelernt. Es klingt ganz ähnlich wie das Fermatsche Prinzip. Diesmal interessieren wir uns aber nicht für den Weg, den das Licht nimmt, sondern für die Bewegung eines Körpers zwischen zwei Punkten A und B. Neben der realen Bewegung müssen wir uns dazu auch alle möglichen fiktiven Bewegungen zwischen den beiden Punkten vorstellen, die nicht unbedingt dem Newtonschen Bewegungsgesetz gehorchen. Dabei wollen wir eine Einschränkung machen: Die Zeitdauer, um von A nach B zu gelangen, soll immer gleich groß sein. Welche Flugbahn nimmt der Körper dann in der Realität?

Reale und fiktive Bewegungen eines Körpers zwischen den Punkten A und B.
Tatsächlich kann man analog zum Fermatschen Prinzip wieder eine Größe finden,
die sich für jede dieser Bewegungskurven berechnen lässt und die bei der
realen Bewegungskurve minimal wird: die sogenannte Wirkung,
die man mit dem Buchstaben \(S\) abkürzt. Dazu berechnet man für jeden Zeitpunkt
die jeweilige kinetische Energie \(T\) und potentielle Energie \(V\) des Körpers
bei der entsprechenden Bewegung, bildet die Differenz
und integriert diese dann über die gesamte Zeit auf:
\[
S = \int_{t_1}^{t_2} (T - V) \, dt
\]
Im Integranden steht dabei übrigens gerade die Lagrange-Funktion
\[
L = T - V
\]
die wir schon kennengelernt haben.
Da sich die kinetischen und potentiellen Energien bei den verschiedenen Bewegungskurven unterscheiden, ergibt sich für jede Bewegungskurve eine andere Wirkung. In der Realität entscheidet sich der Körper dann für den Weg mit der kleinsten Wirkung.
Offenbar gibt es viele Ähnlichkeiten zwischen dem Fermatschen Prinzip für Lichtstrahlen und dem Prinzip der kleinsten Wirkung in der Mechanik. Der Verdacht liegt nahe, dass beide Prinzipien eine gemeinsame Grundlage haben könnten. Diese gibt es tatsächlich, nämlich die Wellennatur von Strahlung und Materie, wie sie bei Teilchen durch die Quantenmechanik beschrieben wird. Doch so naheliegend diese Vermutung auch erscheinen mag – erst Richard Feynman gelang es, daraus eine alternative Sichtweise auf die Quantenmechanik zu entwickeln.
© Jörg Resag, www.joerg-resag.de
last modified on 13 February 2025