
Zusammenfassung des Buchkapitels:
Diracs geniale Idee
Feynman und Wheeler war es also tatsächlich gelungen, die unendliche Selbstwechselwirkung der Elektronen aus der klassischen Elektrodynamik zu verbannen. Nun musste der zweite Schritt folgen: die Übersetzung ihrer Theorie in eine Quantentheorie. Schließlich wollte Feynman ja die Unendlichkeiten in der Quantenelektrodynamik beseitigen.
Dieses Vorhaben erwies sich allerdings als schwierig. Nachdem es dem erfahreneren Wheeler nicht gelungen war, eine Quantenversion ihrer Theorie zu formulieren, machte sich auch Feynman an dieses Problem heran. Doch auch er kam nicht weiter – an Paulis Bedenken war offenbar etwas dran! Die damals bekannten Kochrezepte, mit denen sich eine klassische Theorie normalerweise in eine Quantentheorie umwandeln lässt, funktionierten nicht.
Feynman und Wheeler hatten es immerhin geschafft, eine Wirkung für ihre klassische Theorie zu formulieren und die Bewegungen der Ladungen ohne Felder mit dem Prinzip der kleinsten Wirkung zu beschreiben. Nur wusste niemand, wie man auf Basis einer Wirkung eine zugehörige Quantentheorie formulieren konnte. Da kam der Zufall zu Hilfe: Im Frühjahr 1941 ging Feynman eines Abends zu einer Party in die Nassau-Taverne in Princeton, wo er auf den deutschen Physiker Herbert Jehle traf. So wie viele andere war auch er vor dem Naziterror in Deutschland geflohen. Sie kamen ins Gespräch und Feynman fragte den gut zehn Jahre älteren Jehle, ob er einen Weg wüsste, wie man eine Quantentheorie direkt auf der Wirkung aufbauen könnte
Jehle kannte keinen solchen Weg, doch ihm fiel etwas anderes ein: Paul Dirac hatte bereits im Jahr 1932 eine wenig beachtete Arbeit mit dem Titel The Lagrangian in Quantum Mechanics veröffentlicht, in der er den Zusammenhang zwischen Lagrange-Funktion und Quantenmechanik aufzeigt. Lagrange-Funktion und Wirkung sind, wie wir schon wissen, eng miteinander verwandt, denn die Wirkung ist das Zeitintegral der Lagrange-Funktion über den Bewegungsablauf eines Systems!
Am nächsten Tag gingen die beiden zusammen in die Bibliothek der Universität und Jehle zeigte Feynman die Veröffentlichung von Dirac. Darin ging es um die Frage, wie sich eine Quantenwelle in Analogie zum Huygensschen Prinzip über ein sehr kurzes Zeitintervall fortentwickelt (siehe erste Zusatzinfo unten). Feynman gelang es, an der Tafel aus Diracs Formel die quantenmechanische Schrödinger-Gleichung abzuleiten. Als Jehle dies sah, traute er seinen Augen kaum: Offenbar hatte dieser junge amerikanische Physiker an der Tafel mal eben eine zukunftsweisende Entdeckung gemacht.
Pfadintegrale: ein neuer Zugang zur Quantentheorie
Dank Dirac hatte Feynman nun also eine Verbindung zwischen der quantenmechanischen Wellenfunktion und der klassischen Lagrange-Funktion in der Hand. Konnte er damit auch eine Verbindung zwischen Quantenwellen und der klassischen Wirkung herstellen? Nun, für die Wirkung muss man die Lagrange-Funktion über die Zeit aufintegrieren, d. h., man darf sich nicht nur auf ein sehr kurzes Zeitintervall beschränken, sondern muss auch längere Zeitabschnitte betrachten.
Feynman dachte in den Tagen nach seinem Treffen mit Jehle darüber nach, wie sich das bewerkstelligen ließ, und erkannte schließlich die Lösung: Wenn man sehr viele kurze Zeitintervalle aneinanderfügt und sich so von einem Punkt zum nächsten Punkt, dann weiter zu einem anderen Punkt usw. hangelt, so summieren sich die Schwingungszahlen der einzelnen Elementarwellen, die die Punkte miteinander verbinden. Bei unendlich vielen infinitesimalen Zeitintervallen wird aus der Summe dann ein Zeitintegral über die Lagrange-Funktion entlang des Weges durch die betrachteten Punkte, und das ist dann genau die Wirkung dieses Weges (siehe zweite Zusatzinfo unten).
Daraus lässt sich umgekehrt auch das Prinzip der kleinsten Wirkung ableiten, so wie analog auch das Fermatsche Prinzip für Lichtstrahlen aus dem Verhalten elektromagnetischer Wellen ergibt. An die Stelle der Laufzeit für einen Lichtweg tritt dabei die Wirkung einer Elektronenbahn. Der Wellenbeitrag eines Elektronen-Pfades schwingt dabei so oft auf und ab, wie die Wirkung des Pfades Plancksche Wirkungsquanten enthält. Man spricht hier deshalb auch von sogenannten Pfadintegralen.
Mit seinen Pfadintegralen war es Feynman gelungen, einen vollkommen neuen Zugang zur Quantenmechanik zu finden, der in vielen Aspekten deutlich eleganter war als die bis dahin bekannten Formulierungen. Hat man erst die Wirkung einer klassischen Theorie gefunden, so sollte sich über die Pfadintegrale die zugehörige Quantentheorie formulieren lassen.
Etwas stimmt nicht
Feynman war also zuversichtlich, dass sich mit seiner Methode die Probleme der Quantenelektrodynamik lösen ließen. Ausgerüstet mit seiner neuen Wirkung für Elektronen ohne Selbstwechselwirkung machte er sich ans Werk – und stieß schon wieder auf Probleme. Es war beispielsweise schwierig, den Spin der Elektronen konsistent zu berücksichtigen. Langsam schlich sich bei Feynman das Gefühl ein, dass irgendetwas immer noch nicht stimmte. In seinem Nobelpreisvortrag drückt er es so aus: "I got a kind of funny feeling that things weren't exactly right."
Feynmans ungutes Gefühl war begründet. So lieferte die Quantentheorie mit der Wirkung von Feynman und Wheeler Energiewerte, die durch komplexe Zahlen beschrieben werden mussten. Doch auch in der modernen Physik müssen Energien ganz gewöhnliche reelle Zahlen sein. Komplexe Energiewerte sind ein Zeichen für Instabilitäten in der Theorie.
Außerdem zeigte es sich, dass sich Wahrscheinlichkeiten nicht zu 100 % aufaddierten. Die Wahrscheinlichkeit, dass zumindest irgendetwas geschah, war also nicht 100 %. Das konnte nicht sein. Wolfgang Pauli schien mit seinen Bedenken, die er im Seminar geäußert hatte, Recht zu behalten.
a) Elementarwellen in der Quantenmechanik und komplexe Zahlen
b) Das Pfadintegral in der Quantenmechanik
Wenn Sie die Verbindung zwischen Lagrangefunktion und Quantenmechanik in Detail sehen wollen und keine Angst vor komplexen Zahlen haben, dann könnte diese Zusatzinfo interessant für Sie sein:
Die Wellenfunktion \(\psi\) am Ort \(x'\) zur Zeit \( t + \Delta t \) ergibt sich nach dem Huygensschen Prinzip durch Überlagerung aller Elementarwellen \( K(x',x, \Delta t) \), die zur früheren Zeit \(t\) an allen Orten \(x\) entstehen, wobei die Elementarwellen noch mit der Wellenfunktion am Entstehungsort gewichtet (multipliziert) werden müssen. Die folgende Formel drückt dies mathematisch aus: \[ \psi(x', t + \Delta t) = \] \[ = \int K(x',x, \Delta t) \, \psi(x,t) \, dx \] Man bezeichnet \(K\) auch als Propagator, denn er legt fest, wie die Wellenfunktion propagiert, also sich ausbreitet und weiterentwickelt. Wenn das Zeitintervall \( \Delta t \) sehr klein ist und die Orte \(x\) und \(x'\) entsprechend nahe beieinander liegen, dann ist \(K\) durch folgende Formel gegeben, wie Feynman mithilfe der Idee von Dirac gezeigt hat: \[ K(x',x, \Delta t) = A \, e^{i \, \Delta t \, L / \hbar} \] mit einem passenden Vorfaktor \(A\) sowie \( \hbar = h/(2 \pi) \) und der imaginären Einheit \(i\) mit \( i^2 = -1 \).
Dirac hatte noch etwas ungenau gesagt, \(K\) sei analog zu der e-Funktion rechts, ohne den genauen Proportionalitätsfaktor \(A\) anzugeben.
In der Lagrangefunktion \[ L = T - V \] muss dabei der Ort \(x\) für die Berechnung der potentientiellen Energie \(V\) und die Geschwindigkeit \[ v = \frac{x' - x}{\Delta t} \] für die Berechnung der kinetischen Energie \(T\) verwendet werden.
Übrigens: Wenn Sie mal einen Blick auf das Buchcover werfen, werden Sie oben links in der Ecke folgende Formel an der Tafel hinter Feynman sehen:

Das ist genau die Formel für den Propagator, wobei Feynman statt \( \Delta t \) den Buchstaben \( \epsilon \) verwendet und in der Klammer hinter \(L\) genau angibt, was man für die Geschwindigkeit und den Ort in \(L\) einsetzen muss.
Die Größen \(\psi, K\) und die e-Funktion sind dabei alles komplexe Zahlen, die man sich als Pfeile oder Uhrzeiger in der zweidimensionalen Ebene vorstellen kann (in der folgenden Grafik dargestellt für eine komplexe Zahl \(z = x + i y\) mit reellen Zahlen \(x\) und \(y\), die man auch als Realteil und Imaginärteil von \(z\) bezeichnet):
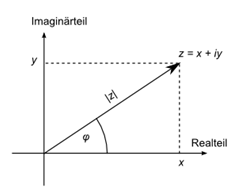
Dabei ist die e-Funktion folgendermaßen definiert: \[ e^{i \varphi} = \cos{\varphi} + i \, \sin{\varphi} \] mit dem reellen Drehwinkel \( \varphi \). Die e-Funktion entspricht also einem Pfeil der Länge 1, der um den Winkel \( \varphi \) gegen den Uhrzeigersinn relativ zur x-Achse gedreht ist. Man kann mit dieser e-Funktion wie mit der gewohnten reellen e-Funktion rechnen.
In der Formel für den Propagator \(K\) oben ist im Bogenmaß der Drehwinkel \( \varphi \) gegeben durch \[ \varphi = \Delta t \, \frac{L}{\hbar} = 2 \pi \cdot n \] mit \[ n = \Delta t \cdot \frac{L}{h} \] Diese reelle Zahl \(n\) gibt also die Anzahl Umdrehungen (Wellen-Schwingungen) an, wobei im Bogenmaß eine volle Umdrehung dem Drehwinkel \( 2 \pi \) entspricht.
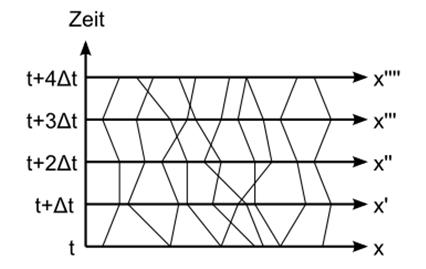
Aus der Summe der Lagrangefunktionen im Exponenten der e-Funktion entsteht dabei das Zeitintegral über die Lagrangefunktion entlang des jeweiligen Weges – also die Wirkung \[ S = \int L \, dt \] des Weges – sodass am Ende gilt:
Der Wellenbeitrag eines jeden Weges im Pfadintegral ist proportional zu \[ e^{i S/\hbar} \] mit der Wirkung \(S\) des jeweiligen Weges. Er besitzt damit \[ n = \frac{S}{h} \] Schwingungen, denn \[ e^{i S/\hbar} = e^{i \, 2 \pi \, S/h} = e^{i \, 2 \pi \, n} \]
© Jörg Resag, www.joerg-resag.de
last modified on 13 February 2025