Es war ein großer Erfolg der theoretischen Physik, als es Niels Bohr im Jahr 1913 erstmals gelang, die Energieniveaus des Elektrons im Wasserstoffatom auszurechnen, wobei er allerdings noch eine Reihe von Ad-hoc-Annahmen für die Elektronenbahnen machen musste. Im Jahr 1926 lieferte dann die Quantenmechanik eine saubere Begründung für die Energieniveaus: Die Elektronen bewegen sich gar nicht auf Bahnen, sondern es bildeten sich im elektrischen Anziehungsfeld des Atomkerns stehende Elektronenwellen, sogenannte Orbitale, aus, ähnlich den Schwingungen auf einer Gitarrensaite.
Die Ergebnisse, die man in der Quantenmechanik mit der nichtrelativistischen Schrödinger-Gleichung erhielt, stimmten schon sehr gut mit den beobachteten Energieniveaus überein. Schaute man allerdings sehr genau hin, so sah man, dass viele Niveaus aus mehreren, sehr eng beieinanderliegenden Einzelniveaus bestanden.
Wenn man die Energieniveaus des Wasserstoffs mit der relativistischen Dirac-Gleichung berechnete, konnte man auch die eng beieinanderliegenden Einzelniveaus gut reproduzieren. Je nachdem, wie der Spin des Elektrons orientiert war, ergaben sich die gemessenen leicht unterschiedlichen Energien. Alles schien also in bester Ordnung zu sein − zumindest im Rahmen der damaligen Messgenauigkeit.
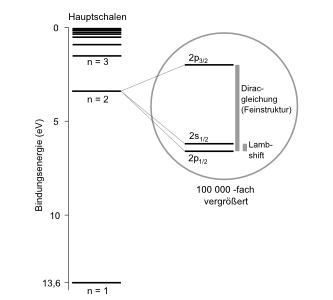
Nach dem Ende des zweiten Weltkrieges war man technisch in der Lage, die Energieniveaus im Wasserstoffatom noch viel genauer zu vermessen als zuvor. Als der amerikanische Physiker Willis Eugene Lamb und sein Doktorand Robert C. Retherford an der Columbia University die Energieniveaus der zweiten Hauptschale im Wasserstoffatom untersuchten, erlebten sie eine Überraschung: Man hatte erwartet, dass es zwei eng benachbarte Energieniveaus in dieser Schale geben sollte − so sagte es die Dirac-Gleichung voraus.
Was Lamb und Retherford jedoch im April 1947 beobachteten, waren drei Niveaus: Das untere Niveau hatte sich noch einmal geringfügig aufgespalten, d. h., die beiden darin enthaltenen Quantenzustände hatten nicht exakt dieselbe Energie. Diese sogenannte Lamb-Shift konnte die Diracgleichung alleine nicht erklären − es musste ein Effekt der Quantenelektrodynamik sein!
Man fand in Rabis Gruppe an der Columbia University (Kusch, Foley und andere) noch ein weiteres Phänomen, das die Diracgleichung nicht erklären konnte: Das magnetische Moment des Elektrons − also seine magnetische Stärke − ist um etwa 0,1 % größer als von der Dirac-Gleichung vorhergesagt.
Oft drückt man das magnetische Moment des Elektrons durch seinen sogenannten g-Faktor aus. Die Diracgleichung sagt dabei den Wert g = 2 voraus. Als man in der der Gruppe von Rabi erstmals wirklich genau hinschaute, fand man eine geringe Abweichung: g ist ein klein wenig größer als zwei, weshalb man auch vom anomalen magnetischen Moment spricht. Moderne Messungen liefern den Wert
wobei die Zahl in Klammern die Unsicherheit in den letzten beiden Stellen angibt. Es ist erstaunlich, wie genau man diese Zahl heutzutage messen kann! Es gibt kaum einen anderen Messwert in der Physik, bei dem man eine ähnliche Genauigkeit erreicht!
Konnte die Quantenelektrodynamik die Lamb-Shift und das magnetische Moment des Elektrons erklären? Das war das große Thema einer kleinen Konferenz, die vom 2. bis 4. Juni 1947 − also nur rund zwei Monate nach der Entdeckung der Lamb-Shift − in einem kleinen Hotel auf Shelter Island stattfand, einer Insel an der östlichen Spitze Long Islands nahe New York. Es war nach dem zweiten Weltkrieg insbesondere für einige junge amerikanische Physiker die erste Gelegenheit, sich über die Grundlagen der Quantentheorie miteinander auszutauschen.
Feynman erinnerte sich später, die Shelter-Island-Konferenz sei die Wichtigste aller Konferenzen gewesen, an denen er je teilgenommen hatte. Hier präsentierten Willis Lamb und Isidor Rabi ihre experimentellen Ergebnisse zur Lamb-Shift und zum g-Faktor des Elektrons und machten damit erstmals eindeutig klar, dass die Dirac-Gleichung unvollständig war. Es gab kleine Korrekturen, die anscheinend durch genau die Effekte in der QED entstanden, die auch die störenden Unendlichkeiten hervorbrachten, nämlich durch die virtuelle Photonenwolke und andere virtuelle Teilchen um das Elektron herum.
Als erster machte sich Hans Bethe nach der Konferenz daran, die von Lamb gemessene Energieverschiebung im Wasserstoffatom auszurechnen. Er war davon überzeugt: Wenn es eine so eindeutig messbare Abweichung von der Dirac-Gleichung gab, dann musste man alles daransetzen, sie auszurechnen.
Bethe wusste zwar nicht, wie man das Elektron im Rahmen der QED relativistisch korrekt beschreiben konnte, aber er kannte sich gut mit dem ausgereiften Instrumentarium der nichtrelativistischen Schrödinger-Gleichung aus und wusste, wie man in diesem Rahmen Strahlungsvorgänge mit relativistischen Photonen beschreiben konnte. Als er nach der Konferenz mit dem Zug von Shelter Island nach Schenectady fuhr, legte er los und hatte am Ende der etwa vierstündigen Zugfahrt tatsächlich eine konkrete Zahl für die Energieverschiebung ausgerechnet. Sie lag sehr nahe am experimentellen Resultat und war ein großer Erfolg für Bethe, was sich schnell herumsprach. Es war sogar fast zu gut, denn in Bethes Rechnung steckte eine windige Annahme, die er vornehmen musste, um die Unendlichkeiten in den Griff zu bekommen: Er nahm an, dass es eine obere Grenze für die Energie der virtuellen Photonen um das Elektron herum geben muss, die ungefähr bei der Elektronenmasse (ausgedrückt in Energieeinheiten) liegen sollte.
Unmittelbar nach seiner Ankunft in Schenectady rief Bethe bei Feynman an und erzählte ihm aufgeregt von seinem Resultat. Zurück in Ithaca hielt Bethe dann einen Vortrag und erläuterte im Detail, wie er die Lamb-Shift mithilfe der nichtrelativistischen Schrödinger-Gleichung näherungsweise berechnet hatte. Dabei äußerte er die Hoffnung, dass seine willkürliche Annahme in einer vollständig relativistischen Rechnung nicht notwendig sei.
Relativistische Rechnungen waren nun Feynmans Spezialgebiet, denn seine Pfadintegrale und Feynman-Diagramme berücksichtigten automatisch die relativistischen Regeln. Also ging er nach der Vorlesung zu Hans Bethe und verkündete optimistisch: „Ich kann das für Dich erledigen. Morgen bringe ich es Dir vorbei!“
Da hatte er den Mund wohl etwas zu voll genommen, denn Feynman stieß auf einige Schwierigkeiten. Nach einigen Wochen hatte er es aber dann geschafft und die Lamb-Shift berechnet, ohne wie Bethe auf ein willkürliches Abschneiden höherer Photonenenergien angewiesen zu sein.
Um mit den Unendlichkeiten in der QED umgehen zu können, muss man sie im ersten Schritt endlich machen − also regularisieren − indem man beispielsweise eine maximale Energie für die virtuellen Photonen im Umfeld des Elektrons einführt wie in Bethes Berechnung der Lamb-Shift. Feynman machte dies sehr geschickt, sodass seine Regularisierung verträglich mit der Relativitätstheorie war.
Feynmans Berechungen lieferten für die Lamb-Shift bzw. den g-Faktor nach der Regularisierung also zunächst eine Summe mathematischer Ausdrücke, von denen einige unendlich werden, wenn man die Maximalenergie der virtuellen Photonen gegen Unendlich gehen lässt. Diese Unendlichkeiten versteckt man im nächsten Schritt in der physikalischen Ladung und in der Masse des Elektrons in der Annahme, dass sie dort durch eine passende nackte Ladung und Masse kompensiert werden − genau das ist die berühmte Renormierung.
Tatsächlich kann man auf diese Weise sämtliche Unendlichkeiten schrittweise zum Verschwinden bringen und erhält einen endlichen Ausdruck für physikalische Größen wie die Lamb-Shift oder den g-Faktor. Man sagt auch, die QED ist renormierbar. Das ist keine Selbstverständlichkeit – es funktioniert nur aufgrund der besonderen Struktur der elektromagnetischen Wechselwirkung. Auch bei der Quantisierung der starken und schwachen Wechselwirkung ist dieses Verfahren erfolgreich, nicht aber bei der Gravitation.
Feynman war nicht sehr glücklich über diese Methode, mit dem man die Unendlichkeiten loswerden konnte. Wir dürfen nicht vergessen, dass sein ursprüngliches Ziel gewesen war, die Unendlichkeiten von Anfang an los zu werden. In seiner Nobelpreisrede sagte Feynman viele Jahre später, er halte die Renormierung nach wie vor lediglich für eine elegante Methode, die Unendlichkeiten unter den Teppich zu kehren.
Mag sein − aber in der Praxis funktioniert diese Methode ganz hervorragend! Beispielsweise kann man mit der QED heutzutage in sehr aufwendigen Rechnungen unter Einbeziehung vieler Feynman-Diagramme den g-Faktor des Elektrons auf etwa zehn Dezimalstellen genau berechnen. Diese Zahl stimmt Stelle für Stelle mit dem experimentell ermittelten Wert überein. Kaum eine andere physikalische Theorie ist so erfolgreich wie die QED!