Zusammenfassung des Buchkapitels:
Warum die meisten Teilchen zerfallen – und manche nicht
Während der Jahre, in denen sich Feynman intensiv mit den Eigenschaften von flüssigem Helium auseinandersetze, behielt er die aktuellen Entwicklungen in der Teilchenphysik weiter im Blick uns sollte schließlich eine Entdeckung zu machen, die er persönlich zu seinen größten Erfolgen zählte.
Den Auftakt bildete im April 1956 die International Conference on High Energy Physics (ICHEP). Dort stand ein Phänomen im Mittelpunkt, das für große Verwirrung sorgte: das sogenannte τ-θ-Rätsel (sprich: "Tau-theta-Rätsel").
Bei diesem Rätsel geht es um den Zerfall der sogenannten K-Mesonen. Sie sind etwa halb so schwer wie ein Proton und leben ungewöhnlich lange. So zerfällt das K+ durchschnittlich erst nach etwa 12 Nanosekunden und lebt damit etwa zweieinhalb Billiarden Mal länger als die etwas schwereren ρ-Mesonen. Woran liegt das?
Warum zerfallen die meisten Teilchen überhaupt? Zunächst spricht eigentlich nichts dagegen, dass beispielsweise auch ein Proton in leichtere Teilchen zerfällt und dabei viel Energie freisetzt. Doch niemand hat bisher einen solchen Prozess beobachtet.
Es muss also irgendein Kriterium geben, das darüber entscheidet, ob ein Teilchen stabil ist oder in leichtere Teilchen zerfällt. Mit dem Wissen aus Kapitel 3 können wir dieses Kriterium recht einfach so formulieren: Es muss ein Feynman-Diagramm für den Zerfall geben, in dem eine der drei fundamentalen Wechselwirkungen (elektromagnetische, schwache oder starke WW) den Zerfall hervorruft (die extrem schwache Gravitation spielt hier keine Rolle). Dabei gilt: je stärker eine WW ist, umso schneller sind die zugehörigen Zerfälle. Das ρ-Meson zerfällt über die starke WW, also extrem schnell. Das neutrale Pion π0 zerfällt elektromagnetisch und damit schon deutlich langsamer. Noch viel langsamer zerfällt das K+-Meson – also muss die schwache WW dafür verantwortlich sein.
Strangeness lässt Teilchen lange leben
Warum kann das K+-Meson nicht viel schneller über die elektromagnetische oder gar die starke WW zerfallen?
Mit unserem heutigen Wissen über die Quarks im Inneren der Mesonen ist die Antwort einfach: Das K+ enthält ein sogenanntes Strange-Antiquark, das sich bei dem Zerfall in ein Up-Antiquark umwandeln muss. Die starke sowie die elektromagnetische Wechselwirkung sind dazu nicht in der Lage, denn sie verändern die Quarksorte nicht.
In den frühen 1950er Jahren waren Quarks noch unbekannt. Der amerikanische Physiker Murray Gell-Mann und sein japanischer Kollege Kazuhiko Nishijima lösten das Problem daher auf andere Weise: Sie nahmen an, dass es eine weitere Quantenzahl geben müsse, der Gell-Mann den vielsagenden Namen Strangeness (Seltsamkeit) gab – Teilchen mit Strangeness heißen entsprechend auch seltsame Teilchen (sie zerfallen eben seltsam langsam). Gell-Mann forderte nun, dass weder die starke noch die elektromagnetische Wechselwirkung die Strangeness der Teilchen in Summe ändern können, während die schwache WW dazu in der Lage ist. Jetzt muss man nur noch dem K+ die Strangeness +1 zuordnen und den Zerfallsprodukten die Strangeness null, und schon kann das K+ nur noch relativ langsam über die schwache WW zerfallen. Natürlich ist die mysteriöse Strangeness nichts anderes als die Zahl der Strange-Antiquarks minus die Zahl der Strange-Quarks, aber das konnten Gell-Mann und Nishijima noch nicht wissen.
Das τ-θ-Rätsel: zwei Teilchen oder nur eines?
Beim sogenannten τ-θ-Rätsel geht es nun um folgendes: Das K+ kann auf mehrere verschiedene Weisen über die schwache Wechselwirkung zerfallen. Dabei können beispielsweise zwei Pionen entstehen, manchmal aber auch drei Pionen.
Das Problem mit diesen Zerfällen entsteht, wenn man annimmt, dass die Naturgesetze nicht davon abhängen, ob man ein Experiment in einem Spiegel betrachtet oder nicht. Dann kann nämlich ein Teilchen, das in zwei Pionen zerfällt, nicht in drei Pionen zerfallen und umgekehrt. Man spricht hier auch von der sogenannten Paritätsregel. Hatte man hier womöglich zwei verschiedene Teilchen (τ und θ genannt) vor sich, die in zwei bzw. drei Pionen zerfielen?
Auf der Rochester-Konferenz 1956 teilte sich Feynman ein Zimmer mit dem Experimentalphysiker Martin Block, der ihn abends fragte: "Warum besteht ihr Leute so auf der Paritätsregel? Vielleicht sind τ und θ dasselbe Teilchen. Was wären die Konsequenzen, wenn die Paritätsregel falsch ist?"
Sind die Naturgesetze spiegelsymmetrisch?
Feynman antwortete, dass es dann eine Möglichkeit gäbe, mithilfe der Naturgesetze ein absolutes Rechts und Links zu definieren – beide wären nicht mehr gleichwertig. Ob das so furchtbar wäre, wusste er nicht zu sagen. Also fragte Feynman am nächsten Tag der Konferenz in die Runde: "Ich stelle diese Frage für Martin Block: Was sind die Konsequenzen, wenn die Paritätsregel falsch wäre?"
Kaum jemand glaubte damals an diese Möglichkeit. Doch die beiden anwesenden jungen chinesisch-amerikanischen Physiker Tsung-Dao Lee und Chen Ning Yang, damals Experten auf diesem Gebiet, nahmen die Frage ernst. Also schlugen sie verschiedene Experimente zur Klärung vor und sprachen mit verschiedenen Experimentalphysikern darüber. Unter ihnen war auch die chinesisch-amerikanische Physikerin Chien-Shiung Wu. Madame Wu, wie sie in Anspielung auf die berühmte Madame Curie auch genannt wurde, verfügte über umfangreiche Erfahrungen auf dem Gebiet der radioaktiven Betazerfälle von Atomkernen. Auf einem solchen Betazerfall basierte auch einer der Vorschläge von Lee und Yang, sodass Chien-Shiung Wu diese Idee gerne aufgriff.
Der Betazerfall wird ebenso wie der K+- Zerfall durch die schwache Wechselwirkung ausgelöst. Dabei wandelt sich in einem radioaktiven Atomkern ein Neutron in ein Proton um, wobei ein hochenergetisches Elektron und ein Elektron-Antineutrino ausgesendet werden. Die hochenergetischen Elektronen lassen sich schon mit einfachen Messgeräten problemlos nachweisen. Die ebenfalls freiwerdenden geisterhaften Antineutrinos bleiben dagegen so gut wie immer unsichtbar.
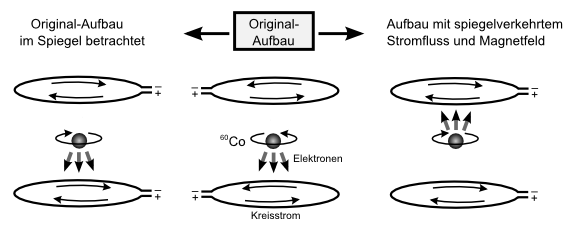
Das Experiment, das Madame Wu sich vorgenommen hatte, basiert auf dem radioaktiven Betazerfall von Cobalt-60-Atomkernen, die sich in Nickel-60-Atomkerne umwandeln. Die Frage, die Wu dabei klären wollte, lautete: Respektiert dieser Zerfall die Paritätsregel und erfolgt spiegelsymmetrisch, d. h. führt ein spiegelverkehrter Messaufbau auch zu einem spiegelverkehrten Messergebnis?
Zur Beantwortung dieser Frage muss man die Rotationsachsen Cobalt-60-Kerne bei sehr tiefen Temperaturen mit einem starken Magnetfeld zunächst parallel ausrichten, Nun ermittelt man, wie viele Elektronen beim Betazerfall der Kerne entlang der Rotationsachse nach oben bzw. nach unten ausgesendet werden.
Die schwache Wechselwirkung verletzt die Spiegelsymmetrie
Was man fand, war eine Überraschung: Die Mehrzahl der Elektronen wurde von den rotierenden Cobalt-60-Kernen nicht gleichmäßig nach oben und unten, sondern nur nach unten ausgesendet, wenn sie von oben gesehen gegen den Uhrzeigersinn rotieren. Wenn wir uns vorstellen, dass die gekrümmten Finger unserer linken Hand die Drehrichtung eines Cobalt-Kerns andeuten, so wurden die Elektronen also bevorzugt in die Richtung des ausgestreckten Daumens emittiert, der nach unten zeigt.
Die Vorzugsrichtung der Elektronen orientiert sich nach dieser Linke-Hand-Regel immer in gleicher Weise an der Rotation der Kerne, die sie aussenden. Damit liefert der spiegelverkehrte Aufbau nicht dasselbe Ergebnis, als würden wir den ursprünglichen Aufbau in einem Spiegel betrachten.

Materie und Antimaterie: der kleine Unterschied
An dieser Stelle können wir ein interessantes Gedankenexperiment anstellen: Angenommen, auf einem fernen Planeten bestünde alles aus Antimaterie statt aus Materie. Wenn nun auf diesem Planeten Madame Anti-Wu auf die Idee käme, dasselbe Experiment wie Madame Wu durchzuführen – nur eben mit Antimaterie – was würde sie feststellen?
Es zeigt sich, dass die ausgesendeten Positronen bevorzugt nach oben emittiert würden, also genau in die andere Richtung als die der Elektronen bei den Cobalt-60-Kernen. Für die Positronen beim Betazerfall der Cobalt-60-Antikerne gilt also eine Rechte-Hand-Regel. Antimaterie verhält sich demnach bei schwachen Zerfällen spiegelverkehrt zu normaler Materie.
Gäbe es die schwache Wechselwirkung nicht, so ließen sich Materie und Antimaterie nicht voneinander unterscheiden, denn die Begriffe der positiven und negativen elektrischen Ladung sind austauschbar und vollkommen willkürlich gewählt. Man nennt dies C-Invarianz, wobei das C für das englische charge conjugation (Ladungsumkehr) steht.
Die schwache Wechselwirkung verletzt diese C-Invarianz, denn das Antimaterie-Universum würde sich beispielsweise beim Betazerfall spiegelverkehrt zum Materie-Universum verhalten. Würde man das Antimaterie-Universum aber in einem Spiegel betrachten, dann würde man keinen Unterschied in den Naturgesetzen mehr sehen – so dachte man zumindest. Man bezeichnet dieses Gesetz als CP-Invarianz, wobei das P für parity oder Parität steht.
Wie man herausfanden, ist auch das Gesetz der CP-Invarianz nicht absolut gültig. Ein im Spiegel betrachtetes Antimaterie-Universum ist nicht in allen Belangen absolut identisch zu einem Materie-Universum. Man muss allerdings schon sehr genau hinschauen bzw. sehr exakt messen, um den Unterschied aufzuspüren.
Was muss man tun, um eine Invarianz zu finden, die nach heutigem Wissen in der Natur uneingeschränkt gilt? Man muss nicht nur Materie durch Antimaterie ersetzen und die Welt spiegeln, sondern man muss zusätzlich auch noch die Zeit rückwärts laufen lassen. Dann sollte sich bei allen grundlegenden Naturgesetzen kein Unterschied zur Ausgangssituation mehr erkennen lassen. Man nennt diese grundlegende Erkenntnis CPT-Invarianz, wobei das T für time steht.
Lee und Yang: Neutrinos sind links
Schon bald nach den Resultaten von Madame Wu wurde die Paritätsverletzung auch in anderen schwachen Zerfallsprozessen nachgewiesen. Lee und Yang nahmen diese Ergebnisse begeistert auf und veröffentlichten im März 1957 eine erste theoretische Erklärung, die auf der folgenden Hypothese basierte:
Neutrinos rotieren in Flugrichtung gesehen immer links herum (und Antineutrinos rechts herum).
Da bei vielen schwachen Zerfällen Neutrinos im Spiel sind, kann man dieses Muster recht oft mit Erfolg anwenden und so die Paritätsverletzung erklären, beispielsweise auch beim Betazerfall. Ausgerechnet beim Zerfall des K+ in zwei oder drei Pionen funktioniert das allerdings nicht, denn hier entstehen keine Neutrinos beim Zerfall.
Feynman: Die schwache Wechselwirkung bevorzugt links
Auf der nächsten Rochester-Konferenz im April 1957 präsentierten Lee und Yang die Ideen aus ihrer gerade erschienenen Veröffentlichung. Feynman nahm ebenfalls wieder an der Konferenz teil. Er analysierte die Ideen von Lee und Yang bis ins Detail und verglich sie mit seinen eigenen Ideen. Mit einem Schlag wurde ihm klar, was in der schwachen Wechselwirkung vor sich geht: Nur die linkshändigen Wellen spielen an den schwachen Vertices eine Rolle!
Konkret bedeutet das: Die schwache Wechselwirkung ist umso stärker bestrebt, ein linkshändiges Teilchen zu erzeugen, je näher dessen Geschwindigkeit nach dem Zerfall der Lichtgeschwindigkeit kommt. Ein (nahezu) masseloses Neutrino wird so gut wie immer linkshändig erzeugt, da es (fast) mit Lichtgeschwindigkeit fliegt.
Feynman stellte über Nacht alle möglichen Berechnungen an und konnte die Ergebnisse von Lee und Yang reproduzieren. Als er allerdings den Betazerfall des Neutrons berechnete, war die Übereinstimmung mit den bekannten Daten weniger gut. Daher verfolgte er die Angelegenheit zunächst nicht weiter und verließ die USA in Richtung Brasilien, wo er den Sommer verbrachte.
Zurück am Caltech unterhielt er sich mit Experimentalphysikern wie Hans Jensen, Aaldert Wapstra und Felix Boehm, die ihm von neuen Resultaten zum Betazerfall des Neutrons berichteten. Diese passten schon viel besser zu Feynmans Theorie.
Feynman war sehr aufgeregt und stürzte sich einmal mehr in eine Nacht voller Berechnungen. Er musste sichergehen, dass seine Theorie funktionierte. Jetzt passte einfach alles. Feynmans Theorie war korrekt! Allerdings waren auch andere Kollegen mittlerweile auf dieselben Ideen gekommen, wenn auch auf andere Weise.
Feynman und Gell-Mann: ein ungleiches Paar
Murray Gell-Mann, der einige Jahre zuvor den Begriff der Strangeness eingeführt hatte, beschäftigte sich ebenfalls intensiv mit dem Problem der Paritätsverletzung und war zu denselben Schlüssen wie Feynman, Marshak und Sudarshan gekommen.
Gell-Mann war etwa zwei Jahre zuvor extra ans Caltech gekommen, um mit Feynman zusammenzuarbeiteten – sein Büro lag in unmittelbarer Nachbarschaft zu Feynmans Büro. Obwohl Gell-Mann im Jahr 1957 mit gerade einmal 27 Jahren elf Jahre jünger war als Feynman, stand er diesem an physikalischer Genialität in nichts nach. Zunächst entwickelte sich eine vielversprechende Zusammenarbeit, in der Dick und Murray, wie viele sie nannten, gemeinsam über den Campus des Caltech streiften und sich stundenlang in intensive Diskussionen verstrickten. Im Lauf der Zeit schlug diese Zusammenarbeit jedoch immer mehr in Rivalität um – zu unterschiedlich waren die Persönlichkeiten dieser beiden großen Physiker.
Zum ersten Mal zeigte sich ihre Rivalität deutlich, als Gell-Mann im Jahr 1957 kurz nach Feynmans Rückkehr aus Brasilien ebenfalls aus seinem Urlaub ans Caltech zurückkehrte. Dort musste er feststellen, dass auch Feynman die korrekte Struktur der schwachen Wechselwirkung erkannt hatte und im Begriff stand, diese zu veröffentlichen. Genau das hatte Gell-Mann ebenfalls vorgehabt.
Um die sich anbahnende Konkurrenz einzudämmen, drängte der Vorsitzende des Physik-Fachbereichs am Caltech, Robert Bacher, Feynman und Gell-Mann dazu, ihre Ideen in einer gemeinsamen Arbeit zu publizieren. Sie ließen sich tatsächlich darauf ein und reichten im September 1957 ihren sechsseitigen Text unter dem Titel Theory of the Fermi Interaction bei Physical Review ein, wo er im Januar 1958 erschien – ein Meilenstein der theoretischen Physik.
a) Spiegelsymmetrie und der Zerfall des geladenen Pions
Die schwache Wechselwirkung ist umso stärker bestrebt, ein linkshändiges Teilchen zu erzeugen, je näher dessen Geschwindigkeit nach dem Zerfall der Lichtgeschwindigkeit kommt.
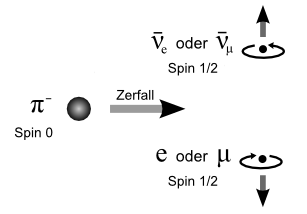
Dieses Verhalten hat beispielsweise zur Folge, dass das negative Pion etwa zehntausendmal häufiger in ein Myon plus Myon-Antineutrino als in ein Elektron plus Elektron-Antineutrino zerfällt. Eigentlich müsste der Zerfall in das leichtere Elektron bevorzugt sein, denn dabei wird fast die gesamte Pion-Masse als Energie freigesetzt, was normalerweise die Wahrscheinlichkeit für einen Zerfall erhöht. Was also ist hier los?
Wenn wir uns das Pion als ruhend vorstellen, so fliegen die beiden beim Zerfall entstehenden Teilchen in entgegengesetzte Richtungen auseinander. Da das Pion Spin Null hat – also keine Eigendrehung besitzt – müssen die beiden Teilchen dabei entgegengesetzt zueinander rotieren, denn als Fermionen tragen sie immer Spin 1/2. In ihrer jeweiligen Flugrichtung betrachtet drehen sie sich also beide zugleich links oder rechts herum. Da sich das Antineutrino immer rechtshändig dreht, muss sich auch das Elektron oder Myon rechtshändig drehen. Ein rechtsdrehendes sehr schnelles Elektron wird von der schwachen Wechselwirkung jedoch nur sehr ungern erzeugt, während ihr dies beim massiveren und damit langsameren Myon eher gelingt.
© Jörg Resag, www.joerg-resag.de
last modified on 19 February 2025