Es ist uns im letzten Kapitel gelungen, den Zusammenhang zwischen Geschwindigkeit und Impuls mit Hilfe der Galileitransformation herzuleiten.
Wir wollen nun eine weitere Erhaltungsgröße kennenlernen: die Energie, oder genauer: die Bewegungsenergie oder kinetische Energie eines Teilchens.
Aber wie kommen wir auf die Idee, dass es eine solche Größe geben könnte?
Auf die Idee, den Impuls als sinnvolle physikalische Größe zu fordern, waren wir durch die genaue Beobachtung von Zusammenstößen zwischen Bällen gekommen. Hier gab es offensichtlich Regeln für die Geschwindigkeiten und Flugrichtungen, die bei solchen Zusammenstößen auftreten können, und wir hatten versucht, diese Regeln durch das Gesetz der Impulserhaltung zu formulieren.
Das Gesetz der Impulserhaltung zusammen mit dem Gesetz für die Addition von Massen (für zusammengesetzte Objekte) und der Formel \(\boldsymbol{p} = m \boldsymbol{v}\) reicht aus, um Kollisionen zwischen Objekten bei niedrigen Geschwindigkeiten (deutlich kleiner als die Lichtgeschwindigkeit) gut zu beschreiben. Das zeigen die Experimente. Die Regeln für die auftretenden Geschwindigkeiten scheinen voll erfasst zu werden.
Wozu also noch eine weitere Erhaltungsgröße?
Die Frage ist berechtigt, und tatsächlich brauchen wir auch keine weitere Erhaltungsgröße.
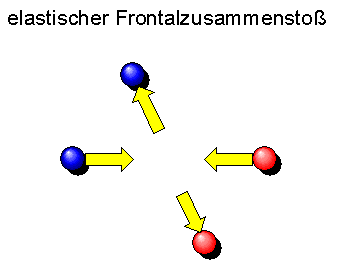
Es gibt jedoch eine ganz bestimmte Sorte von Zusammenstößen, bei denen eine zusätzliche Regel wirksam ist, die über die Impulserhaltung hinausgeht. Wir nennen wollen diese speziellen Zusammenstöße als elastische Stoßvorgänge bezeichnen. Sie treten z.B. auf, wenn wir Bälle aus sehr elastischem Gummi (Flummis) zusammenstoßen lassen.
Lassen wir zwei solche Gummibälle mit gleich großem Impuls frontal zusammenstoßen,
so sind die Impulse nach dem Zusammenstoß genauso groß wie vor dem Zusammenstoß.
Nur die Flugrichtung der Flummis hat sich geändert, nicht aber der Betrag der
einzelnen Impulse. Wir wollen diese speziellen Zusammenstöße als
elastische Frontalzusammenstöße bezeichnen.

Bei frontalen Stoßvorgängen zwischen zwei nicht so elastischen Bällen ist dagegen der Impulsbetrag jedes Balles nach dem Zusammenstoß kleiner als vor dem Zusammenstoß. Die Gesamtsumme der Impulse bleibt jedoch erhalten – sie ist beim Frontalzusammenstoß immer Null, egal ob elastisch oder nicht.
Wenn wir die Galileigruppe als physikalische Symmtriegruppe ansehen, so wollen wir alle Zusammenstöße als elastisch bezeichnen, die durch eine Galileitransformation aus einem elastischen Frontalzusammenstoß hervorgehen können. Das ist unsere Definition für den Begriff elastischer Stoßvorgang.
Die Forderung, dass bei einem elastischen Frontalzusammenstoß sich die Impulsbeträge nicht ändern, lässt sich auch anders formulieren:
Wir wollen jedem elastischen Ball eine stetige, streng monoton wachsende Funktion \(h_i\) zuordnen. Wie diese Funktion im Einzelnen aussieht, lassen wir noch offen. Verschiedene Bälle dürfen dabei auch verschiedene Funktionen zugeordnet haben. Deshalb haben wir auch den Index \(i\) an der Funktion angebracht, wobei \(i\) für die Nummer des betrachteten Balls steht. Wir können mit Hilfe der Funktion \(h_i\) aus dem Impulsquadrat \(p_i^2\) des Balles die Zahl \(h_i(p_i^2)\) berechnen. Die Impulsbeträge haben wir ohne Fettdruck geschrieben, d.h. \( p_i = |\boldsymbol{p}_i| \) und \( p_i^2 = \boldsymbol{p}_i^2 \).
Machen wir nun einen Versuch: Wir betrachten Frontalzusammenstöße von zwei Bällen (nummeriert durch \(i = 1\) und \(i = 2\)), die nicht unbedingt elastisch sein müssen (aber elastisch sein können). Was geschieht nun, wenn wir die Forderung \[ h_1(p_1^2) + h_2(p_2^2) = h_1(p_1'^2) + h_2(p_2'^2) \] für die Impulse bei diesen Zusammenstößen aufstellen? Dabei sind \(\boldsymbol{p}_i'\) die Impulse nach dem Zusammenstoß.
Zunächst einmal sind bei einem Frontalzusammenstoß \[ \boldsymbol{p}_1 = -\boldsymbol{p}_2 = :\boldsymbol{p} \] \[ \boldsymbol{p}_1' = -\boldsymbol{p}_2' = :\boldsymbol{p}' \] Daher vereinfacht sich die Gleichung zu \[ h_1(p^2) + h_2(p^2) = h_1(p'^2) + h_2(p'^2) \] Nehmen wir an, \(p^2\) wäre größer als \(p'^2\). Da \(h_i\) eine streng monoton wachsende Funktionen sein sollen, ist dann auch \(h_i(p^2)\) größer als \(h_i(p'^2)\), so dass die Gleichung nicht mehr erfüllt wäre. Also kann \(p^2\) nicht größer als \(p'^2\) sein.
Analog folgern wir, dass auch \(p'^2\) nicht größer als \(p^2\) sein kann, wenn die Gleichung mit streng monoton wachsenden Funktionen \(h_i\) gelten soll.
Damit muss \(p'^2 = p^2\) sein! Der frontale Zusammenstoß muss elastisch sein.
Wir haben also gezeigt:
Das können wir nun nutzen, um von frontalen elastischen Zusammenstößen zu beliebigen (auch nicht frontalen) elastischen Zusammenstößen überzugehen.
Wir hatten elastische Stoßvorgänge so definiert, dass sie durch eine Galileitransformation aus einem elastischen Frontalzusammenstoß hervorgehen. Können wir eine dazu gleichwertige Definition mit Hilfe der Funktionen \(h_i\) aufstellen?
Um das zu erreichen, müssen wir bestimmte Eigenschaften für \(h_i\) fordern. Die Impulsfunktion \(h_i\) muss verträglich mit den Galileitransformationen sein. Genauer bedeutet das: Da für die Impulse zweier Teilchen bei einem frontalen elastischen Zusammenstoß die Gleichung \[ h_1(p^2) + h_2(p^2) = h_1(p'^2) + h_2(p'^2) \] gilt, so soll diese Gleichung auch für alle Impulse gelten, die durch Galileitransformationen aus den Impulsen \(\boldsymbol{p}\) und \(\boldsymbol{p}'\) hervorgehen, und umgekehrt.
Was bringt uns diese Forderung? Um das zu sehen, wollen wir einen kurzen Zwischenschritt machen: Man kann nämlich die Impulse eines beliebigen Zusammenstoßes zweier Teilchen generell durch eine Galileitransformation aus den Impulsen eines Frontalzusammenstoßes erhalten. Um das zu sehen, suchen wir einfach die inverse Galileitransformation, die unsere Impulse in die Impulse eines Frontalzusammenstoßes umwandelt. Wegen der Gruppenstruktur der Galileigruppe kann man dann auch leicht die zugehörige Galileitransformation angeben, die die Impulse des Frontalzusammenstoßes in die vorgegebenen Impulse umwandelt.
Aus dem Impuls \( \boldsymbol{p}_i = m_i \boldsymbol{v}_i\) wird durch eine Galileitransformation der Impuls \[ m_i \boldsymbol{u} + R \boldsymbol{p}_i \] Die transformierten Impulse sollen die Impulse eines Frontalzusammenstoßes sein, d.h. es soll gelten: \[ m_1 \boldsymbol{u} + R \boldsymbol{p}_1 + m_2 \boldsymbol{u} + R \boldsymbol{p}_2 = 0 \] und somit \[ \boldsymbol{u} \, (m_1 + m_2) + R \, (\boldsymbol{p}_1 + \boldsymbol{p}_2) = 0 \] Man kann diese Gleichung nach \(\boldsymbol{u}\) freistellen mit dem Ergebnis \[ \boldsymbol{u} = \frac{R \, (\boldsymbol{p}_1 + \boldsymbol{p}_2)}{m_1 + m_2} \] Jede Galileitransformation mit eine solchen \(\boldsymbol{u}\) (z.B. mit \(R = \mathbb{1}\)) leistet also das gewünschte und wandelt die Impulse \(\boldsymbol{p}_1\) und \(\boldsymbol{p}_2\) in die Impulse eines Frontalzusammenstoßes um. Die Umkehrtransformation erzeugt daher die Impulse \(\boldsymbol{p}_1\) und \(\boldsymbol{p}_2\) aus den Impulsen eines Frontalzusammenstoßes.
Wegen der Impulserhaltung für die Impulse vor und nach der Kollision \[ \boldsymbol{p}_1 + \boldsymbol{p}_2 = \boldsymbol{p}_1' + \boldsymbol{p}_2' \] wandelt die gleiche Galileitransformation auch die Impulse nach dem Zusammenstoß in die Impulse nach dem Frontalzusammenstoß um (denn in der obigen Formel für \(\boldsymbol{u}\) kommt gerade die Summe der Impulse vor).
Nun sind wir für die folgende Argumentation gerüstet: Wenn für die Impulse bei einem Zusammenstoß die Gleichung \[ h_1(p_1^2) + h_2(p_2^2) = h_1(p_1'^2) + h_2(p_2'^2) \] gilt, und wenn die Impulse durch eine Galileitransformation aus den Impulsen eines Frontalzusammenstoßes hervorgehen (was ja immer geht, wie wir gerade gezeigt haben), so gilt nach unserer Forderung an die Funktionen \(h_i\) auch für die Impulse dieses Frontalzusammenstoßs die Geichung \[ h_1(p^2) + h_2(p^2) = h_1(p'^2) + h_2(p'^2) \] d.h. es handelt sich um einen elastischen Frontalzusammenstoß.
Das bedeutet: Wenn für die Impulse bei einem Zusammenstoß die Gleichung \[ h_1(p_1^2) + h_2(p_2^2) = h_1(p_1'^2) + h_2(p_2'^2) \] gilt, so handelt es sich um einen elastischen Stoßvorgang, und umgekehrt, sofern \(h_i\) die oben gestellte Forderung erfüllt.
Man kann auch sagen: ein elastischer Stoßvorgang ist dadurch gekennzeichnet, dass die Summe der Funktionswerte \(h_i(p_i^2)\) sich durch den Zusammenstoß nicht ändert. Die Summe dieser Funktionswerte bildet eine Erhaltungsgröße bei elastischen Stoßvorgängen.
Bleibt also die Aufgabe, diese Funktionen \(h_i\) anhand der gestellten Forderung zu finden.
Die Forderung lautete: Wenn für die Impulse zweier Teilchen bei einem frontalen Zusammenstoß die Gleichung \[ h_1(p^2) + h_2(p^2) = h_1(p'^2) + h_2(p'^2) \] gilt (d.h. \(p^2 = p'^2\), wie wir von oben wissen), so muss diese Gleichung auch für alle Impulse gelten, die durch Galileitransformationen aus den Impulsen \(\boldsymbol{p}\) und \(\boldsymbol{p}'\) hervorgehen, und umgekehrt.
Es muss also gelten: \[ \quad \quad h_1((m_1\boldsymbol{u}+R\boldsymbol{p}_1)^2) + h_2((m_2\boldsymbol{u}+R\boldsymbol{p}_2)^2) = \] \[ = h_1((m_1\boldsymbol{u}+R\boldsymbol{p}_1')^2) + h_2((m_2\boldsymbol{u}+R\boldsymbol{p}_2')^2) \] Dabei ist \[ \boldsymbol{p}_1 = - \boldsymbol{p}_2 = : \boldsymbol{p} \] \[ \boldsymbol{p}_1' = - \boldsymbol{p}_2' = : \boldsymbol{p}' \] mit \[ p^2 = p'^2 \] also \[ p = p' \] (wir setzen voraus, dass diese Impulsbeträge positiv sind).
Um die Schreibweise etwas zu vereinfachen, definieren wir die Einheitsvektoren mit Länge 1 in Richtung von \(\boldsymbol{p}\) und \(\boldsymbol{p}'\), also \[ \boldsymbol{e} = \frac{\boldsymbol{p}}{p} \] \[ \boldsymbol{e} = \frac{\boldsymbol{p}'}{p'} \] Es ist also \begin{align} \boldsymbol{p}_1 &= p \, \boldsymbol{e} \\ \boldsymbol{p}_2 &= - p \, \boldsymbol{e} \\ \boldsymbol{p}_1' &= p \, \boldsymbol{e}' \\ \boldsymbol{p}_2' &= - p \, \boldsymbol{e}' \end{align} Wir führen die Impulsquadrate in den \(h_i\) aus und erhalten \[ \; h_1((m_1^2 u^2 + p^2 + 2 m_1 p \boldsymbol{u} (R\boldsymbol{e})) + \] \[ + h_2((m_2^2 u^2 + p^2 - 2 m_2 p \boldsymbol{u} (R\boldsymbol{e})) = \] \[ = h_1((m_1^2 u^2 + p^2 + 2 m_1 p \boldsymbol{u} (R\boldsymbol{e}')) + \] \[ + h_2((m_2^2 u^2 + p^2 - 2 m_2 p \boldsymbol{u} (R\boldsymbol{e}')) \] Das ist unsere Ausgangsgleichung (A) (dabei haben wir \(R^T \, R = \mathbb{1} \) verwendet, sodass \( (R \boldsymbol{p})^2 = p^2 \) ist).
Die Ableitung dieser Gleichung nach den Komponenten \(u_j\) des Vektors \(\boldsymbol{u}\) an der Stelle \(\boldsymbol{u} = 0\) (so dass die inneren Ableitungen der \(u^2\)-Terme wegfallen) ergibt \[ \; h_1'(p^2) \, (2 m_1 p (R\boldsymbol{e})_j) + \] \[ - h_2'(p^2) \, (2 m_2 p (R\boldsymbol{e})_j) = \] \[ = h_1'(p^2) \, (2 m_1 p (R\boldsymbol{e}')_j) + \] \[ - h_2'(p^2) \, (2 m_2 p (R\boldsymbol{e}')_j) \; \]
mit der Schreibweise \[ h_i'(p^2) := \frac{d}{dx} h(x) \bigg|_{x = p^2} \]
Diese Gleichung soll richtig sein für alle Einheitsvektoren \(\boldsymbol{e}\) und \(\boldsymbol{e}'\). Beide Seiten müssen gleich Null sein, damit dies erfüllt ist, denn zwei Vektoren sind nur dann bei beliebiger Ausrichtung immer gleich groß, wenn sie Null sind. Also ist \[ h_1'(p^2) \, 2 m_1 p - h_2'(p^2) \, 2 m_2 p = 0 \] oder einfacher \[ m_1 \, h_1'(p^2) = m_2 \, h_2'(p^2) \] Diese Gleichung soll für alle Massenwerte \(m_i\) richtig sein. Beide Seiten können damit nicht von der Masse \(m_i\) oder vom Teilchenindex \(i\) abhängen, sondern nur vom Impuls. Also ist \( m_i \, h_i'(p^2) \) eine Funktion des Impulsbetrags \(p\), die unabhängig von der Masse \(m_i\) und dem Teilchenindex \(i\) ist. Wir wollen diese Funktion mit \(a(p^2)\) bezeichnen, also \[ m_i \, h_i'(p^2) = a(p^2) \] Dies ist unsere Zwischengleichung (B).
Wir wollen noch eine zweite Zwischengleichung herleiten, indem wir unsere Ausgangsgleichung (A) nach \(p\) an der Stelle \(p = 0\) ableiten. Hier nochmal die Ausgangsgleichung (A): \[ \; h_1((m_1^2 u^2 + p^2 + 2 m_1 p \boldsymbol{u} (R\boldsymbol{e})) + \] \[ + h_2((m_2^2 u^2 + p^2 - 2 m_2 p \boldsymbol{u} (R\boldsymbol{e})) = \] \[ = h_1((m_1^2 u^2 + p^2 + 2 m_1 p \boldsymbol{u} (R\boldsymbol{e}')) + \] \[ + h_2((m_2^2 u^2 + p^2 - 2 m_2 p \boldsymbol{u} (R\boldsymbol{e}')) \] Ableiten nach \(p\) an der Stelle \(p = 0\) ergibt \[ \; h_1'(m_1^2 u^2) \, (2 m_1 \boldsymbol{u} (R\boldsymbol{e})) + \] \[ - h_2'(m_2^2 u^2) \, (2 m_2 \boldsymbol{u} (R\boldsymbol{e})) = \] \[ = h_1'(m_1^2 u^2) \, (2 m_1 \boldsymbol{u} (R\boldsymbol{e}')) + \] \[ - h_2'(m_2^2 u^2) \, (2 m_2 \boldsymbol{u} (R\boldsymbol{e}')) \; \] Wieder soll diese Gleichung richtig sein für alle Einheitsvektoren \(\boldsymbol{e}\) und \(\boldsymbol{e}'\), d.h. beide Seiten müssen wieder gleich Null sein. Es gilt also \[ m_1 \, h_1'(m_1^2 u^2) = m_2 \,h_2'(m_2^2 u^2) \] Unserer Zwischengleichung (B) sagt nun, dass \(m_i \, h_i'(p^2) = a(p^2)\) ) ist, also eine Funktion unabhängig vom Teilchenindex \(i\). Das gilt für alle Impulsbeträge \(p\), also auch für \(p = m_i u\). Die obige Gleichung sagt also: \[ a(m_1^2 u^2) = a(m_2^2 u^2) \] Diese Gleichung soll für beliebige Werte von \(m_i\) gelten. Die Funktion \(a\) muss also unabhängig von ihrem Argument sein, d.h. sie ist konstant. Wir wollen diese Konstante als \(A\) bezeichnen. Es ist also \[ a(p^2) = A \] Setzen wir dieses Ergebnis in unsere Zwischengleichung (B) ein – hier ist sie nochmal: \[ m_i \, h_i'(p^2) = a(p^2) \] Einsetzen von \(a(p^2) = A\) ergibt \[ m_i \, h_i'(p^2) = A \] Wir stellen nach \(h'(p^2)\) frei: \[ h_i'(p^2) = \frac{A}{m_i} \] Die Stammfunktion der konstanten Funktion \(h_i'(x) = \frac{A}{m_i}\) lautet \(h_i(x) = \frac{A}{m_i}x + B_i\) mit einer Integrationskonstanten \(B_i\). Einsetzen von \(x = p^2\) ergibt \[ h_i(p^2) = \frac{A}{m_i} p^2 + B_i \] Es ist uns also gelungen, eine Funktion herzuleiten, die die gewünschten Eigenschaften besitzt! Man bezeichnet diese Funktion auch als die kinetische Energie oder auch Bewegungsenergie des Teilchens. Bei elastischen Stößen ist die Summe der Bewegungsenergien also eine Erhaltungsgröße!
Drei Dinge sind an diesem Ergebnis besonders interessant:
Die Tatsache, dass in unserer Herleitung die additive Konstante \(B_i\) in der Energie auftaucht, kommt daher, dass sie beim elastischen Zwei-Teilchen-Stoß in der Energieerhaltung auf beiden Seiten der Gleichung auftaucht und sich weghebt.
In der nichtrelativistischen Physik wählt man üblicherweise die Werte \(A = \frac{1}{2}\) und \(B_i = 0\) für die obigen Konstanten.
Den Wert \(B_i = 0\) wählt man einfach deshalb, damit die kinetische Energie für ein ruhendes Teilchen gleich Null wird. In der Relativitätstheorie würde man dagegen \(B_i = m_i c^2\) als sogenannte Ruheenergie wählen – mehr dazu in einem späteren Kapitel.
Um die Wahl \(A = \frac{1}{2}\) zu verstehen, müssen wir noch einmal auf den Begriff der Kraft zurückkommen.
Bislang sind wir völlig ohne diesen Begriff ausgekommen. Wir haben lediglich die freie Bewegung von Objekten vor und nach einem Zusammenstoß untersucht und uns für eine detaillierte Beschreibung des Zusammenstoßes selbst nicht interessiert.
Wenn wir dagegen eine solche detaillierte Beschreibung des Stoßprozesses haben wollen, so müssen wir uns fragen, wie die Teilchen in ihrer geradlinig-gleichförmigen Bewegung gestört werden. Wie verändern sich die Impulse der Teilchen beim Zusammenstoß?
Wir interessieren uns also für die zeitliche Ableitung der Impulse der Teilchen. Dabei war unsere Grundvoraussetzung: wenn nichts auf die Teilchen einwirkt, dann ist die zeitliche Ableitung der Impulse gleich Null. Demnach liegt es nahe, umgekehrt zu sagen, dass etwas auf die Teilchen wirkt, wenn der Impuls sich ändert. Wir wollen sagen, dass eine Kraft \(\boldsymbol{F}\) auf die Teilchen wirkt, und dass die zeitliche Impulsänderung gerade gleich dieser Kraft ist: \[ \frac{d}{dt} \boldsymbol{p} = \boldsymbol{F} \] Mit \(\boldsymbol{p} = m \boldsymbol{v}\) ergibt sich daraus die Newtonsche Grundgleichung der Mechanik \(\boldsymbol{F} = m \boldsymbol{a}\).
Man könnte diese Gleichung als Definition der Kraft auffassen, aber es steckt mehr dahinter, wie wir im ersten Kapitel bereits diskutiert haben. Sinn macht die Gleichung erst, wenn wir weitere Informationen über die Kraft haben, z.B. wenn sie als Funktion des Teilchenabstandes beim Zusammenstoß beschrieben werden kann.
Die kinetische Energie eines Teilchens wird in der physikalischen Literatur üblicherweise über den Kraftbegriff eingeführt. Man stellt sich vor, dass eine Kraft auf ein anfangs ruhendes Teilchen wirkt und es beschleunigt. Man definiert nun die kinetische Energie E des Teilchens als das Integral der Kraft entlang des zurückgelegten Wegs: \[ E = \int_{\mathrm{Weg}} \boldsymbol{F} \, \boldsymbol{ds} \] Die folgende kleine Rechnung (in etwas schlampiger Physikernotation) ergibt für eine Bewegung, die mit einem ruhenden Teilchen startet und einer Kraft, die dieses in eine feste Richtung beschleunigt: \[ E = \int \boldsymbol{F} \, \boldsymbol{ds} = m \int \frac{\boldsymbol{dv}}{dt} \, \boldsymbol{ds} = \] \[ = m \int \boldsymbol{dv} \, \frac{\boldsymbol{ds}}{dt} = m \int \boldsymbol{dv} \, \boldsymbol{v} = \] \[ = \frac{m}{2} v^2 + B = \frac{p^2}{2m} + B \] Man sieht, wie der Faktor \(A = \frac{1}{2}\) zustande kommt, wenn man die kinetische Energie über den Kraftbegriff einführt.
Kommen wir noch einmal zurück zur detaillierten Beschreibung des Zusammenstoßes zweier Teilchen mit Hilfe des Kraftbegriffs.
Wir wollen uns den Zusammenstoß zwischen zwei Teilchen so vorstellen, dass eine Kraft zwischen den Teilchen wirkt, solange die Teilchen relativ nahe zusammen sind. In vielen Fällen kann man mit einem Ansatz der Form \[ \boldsymbol{F}_{ij} = (\boldsymbol{x}_i - \boldsymbol{x}_j) \, f(|\boldsymbol{x}_i - \boldsymbol{x}_j|) \] diese Kraft recht gut beschreiben, wobei die Teilchenindices \(i\) und \(j\) die Werte 1 und 2 bzw. 2 und 1 annehmen. Dabei ist \(\boldsymbol{F}_{ij}\) die Kraft, die Teilchen \(j\) auf Teilchen \(i\) ausübt, also \[ \frac{d}{dt} \boldsymbol{p}_i = \boldsymbol{F}_{ij} \] Der Vektor \(\boldsymbol{x}_i\) gibt dabei den Ort von Teilchen \(i\) an.
Wie man sieht, erfüllt der Ansatz die Gleichung (actio gleich reactio) \[ \boldsymbol{F}_{12} = - \boldsymbol{F}_{21} \] so dass sich die Impulse immer entgegengesetzt zueinander ändern und die Impulserhaltung zu jedem Zeitpunkt erfüllt ist.
An dieser Stelle tritt nun eine wichtige Frage auf: ist der obige Ansatz für die Kraft zwischen zwei Teilchen verträglich mit der Galileigruppe als physikalischer Symmetriegruppe?
Präzisieren wir zunächst, was wir mit diesem Satz genau meinen.
Angenommen, durch die Gleichung \[ \frac{d}{dt} \boldsymbol{p}_1 = - \frac{d}{dt} \boldsymbol{p}_2 = \boldsymbol{F}_{12} = \] \[ = (\boldsymbol{x}_1 - \boldsymbol{x}_2) \, f(|\boldsymbol{x}_1 - \boldsymbol{x}_2|) \] wird ein physikalisch beobachteter Zusammenstoß zwischen zwei gegebenen Objekten beschrieben. Wenn die Galileigruppe eine Symmetriegruppe der Physik ist, so kann man die Orte und Impulse über eine Galileitransformation in neue Orte und Impulse umrechnen und erhält wieder einen physikalisch möglichen Zusammenstoß zwischen den beiden gegebenen Objekten. Diese neuen Orte und Impulse müssen nun ebenfalls die obige Gleichung erfüllen, wenn diese Gleichung jeden physikalisch möglichen Zusammenstoß zwischen den beiden Objekten beschreiben soll.
Setzen wir also die transformierten Orte \( \boldsymbol{u} t + R \boldsymbol{x}_i + \boldsymbol{b} \) und Impulse \(m_i \boldsymbol{u} + R \boldsymbol{p}_i \) in die Gleichung ein und überprüfen, was passiert. Für die Impulsableitungen erhält man (da \(\boldsymbol{u}\) und \(R\) nicht von der Zeit abhängen) \[ \frac{d}{dt} (m_i \boldsymbol{u} + R \boldsymbol{p}_i) = R \, \frac{d}{dt} \boldsymbol{p}_i \] und für den Kraftterm ergibt sich \[ ( ( \boldsymbol{u} t + R \boldsymbol{x}_1 + \boldsymbol{b}) - ( \boldsymbol{u} t + R \boldsymbol{x}_2 + \boldsymbol{b})) \cdot \] \[ \cdot f(|(\boldsymbol{u} t + R \boldsymbol{x}_1 + \boldsymbol{b}) - ( \boldsymbol{u} t + R \boldsymbol{x}_2 + \boldsymbol{b})|) = \] \[ = R \, (\boldsymbol{x}_1 - \boldsymbol{x}_2) \, f(| R \, (\boldsymbol{x}_1 -\boldsymbol{x}_2)|) \] Wenn Impulsableitungen und Kraftterm nach der Galilei-Transformation gleich sein sollen, muss also gelten: \[ R \, \frac{d}{dt} \boldsymbol{p}_1 = R \, (\boldsymbol{x}_1 - \boldsymbol{x}_2) \, f(| R \, (\boldsymbol{x}_1 -\boldsymbol{x}_2)|) \] Die Matrix \(R\) kann man wegkürzen, außer im Argument von \(f\). Dort kann man \(R\) nur dann weglassen, wenn \(R\) eine orthogonale Matrix ist, also wenn \(R\) räumliche Abstände nicht ändert. In diesem Fall ist die obige Gleichung gleich der Gleichung für die Orte und Impulse vor der Transformation, und die hatten wir als gültig vorausgesetzt.
Fassen wir noch einmal zusammen:
Wenn jeder physikalisch beobachtete Zusammenstoß zwischen zwei Objekten durch die Gleichung \[ \frac{d}{dt} \boldsymbol{p}_1 = - \frac{d}{dt} \boldsymbol{p}_2 = \boldsymbol{F}_{12} = \] \[ = (\boldsymbol{x}_1 - \boldsymbol{x}_2) \, f(|\boldsymbol{x}_1 - \boldsymbol{x}_2|) \] beschrieben wird, und wenn jede Galileitransformation eine Symmetrietransformation ist (d.h. die Galilei-transformierten Orte und Impulse eines physikalisch beobachteten Zusammenstoßes der zwei Objekte gehören wieder zu einem physikalisch möglichen Zusammenstoß), dann muss die Matrix \(R\) eine orthogonale Matrix sein, also eine Drehung (ggf. verknüpft mit einer Raumspiegelung).
Es ist interessant, dass erst die konkrete Form eines Kraftgesetzes uns zu dieser Einschränkung zwingt. Die Impulserhaltung alleine hatte uns nicht dazu gezwungen (\(R\) musste da nur invertierbar sein). Für unsere Ausgangsgleichung (A) bei der Herleitung der Energieformel haben wir allerdings ebenfalls \(R\) als orthogonale Matrix vorausgesetzt.
© Jörg Resag, www.joerg-resag.de
last modified on 20 June 2023