Wie sieht nun der Hamiltonoperator und damit die zeitliche Dynamik einer Quantentheorie konkret aus?
Das hängt von der jeweils betrachteten physikalischen Quantentheorie ab. Im allgemeinen muss man zur Formulierung einer solchen Theorie zunächst festlegen, welches die grundlegenden dynamischen Größen der Theorie sein sollen. Diese Größen werden durch Operatoren im Hilbertraum dargestellt. Wir werden unten Beispiele für solche Größen kennenlernen. Mit Hilfe dieser Größen kann man nun einen Hamiltonoperator konstruieren und so die zeitliche Dynamik der Zustände festlegen.
Bei der Wahl der dynamischen Größen und der anschließenden Konstruktion des Hamiltonoperators lässt man sich meist von Analogien zu klassischen Nicht-Quantentheorien leiten, z.B. durch Analogien zur klassischen Mechanik (ohne Relativitätstheorie) oder zur Elektrodynamik (der relativistsichen Theorie der elektromagnetischen Felder). Man versucht gleichsam, eine quantisierte Version der klassischen Theorie zu konstruieren, wobei man fordert, dass beim Zusammenwirken sehr vieler Quantenzustände unter bestimmten Bedingungen (Stichwort: Wirkung sehr viel größer als das Plancksche Wirkungsquantum) die Quantentheorie die Eigenschaften der klassischen Theorie reproduziert. Die quantenmechanischen Mittelwerte müssen sich beim Grenzübergang zur klassischen Theorie wie die zugehörigen klassischen Größen verhalten.
Schauen wir uns am Beispiel der nichtrelativistischen Mechanik einmal an, wie ein solcher Übergang von einer klassischen Theorie zu einer Quantentheorie aussehen kann. Die Raum-Zeit-Symmetriegruppe ist dabei nicht die Poincaregruppe, sondern die Galileigruppe – dies ist aber an dieser Stelle nicht weiter wichtig.
In der nichtrelativistischen Mechanik wird die Dynamik durch das Newtonsche Bewegungsgesetz \[ \boldsymbol{F} = m \boldsymbol{a} \] bestimmt, d.h. ein Objekt (Teilchen) mit Masse \(m\) erfährt unter einer Kraft \(\boldsymbol{F}\) eine Beschleunigung \(\boldsymbol{a}\) (mit dem Fettdruck kennzeichnen wir wieder dreidimensionale Vektoren im Raum). Das Objekt durchläuft dabei eine Bahnkurve im dreidimensionalen Raum, die man durch eine Funktion \( \boldsymbol{x}(t) \) mathematisch beschreibt – \( \boldsymbol{x}(t) \) ist der Ort des Objektes zur Zeit \(t\). Die dynamischen Variablen (Freiheitsgrade) der klassischen Mechanik eines Teilchens sind daher gerade die drei Koordinaten des Vektors \( \boldsymbol{x}(t) \). Die Beschleunigung \( \boldsymbol{a} \) ist dabei die zweite zeitliche Ableitung dieser Funktion \( \boldsymbol{x}(t) \): \[ \boldsymbol{a} = \frac{d^2}{dt^2} \, \boldsymbol{x}(t) \]
Wir wollen die Diskussion etwas vereinfachen und annehmen, dass die Kraft \(\boldsymbol{F}\) eine sogenannte konservative Kraft ist, sich also als Gradient eines Potentials \(V(\boldsymbol{x})\) schreiben lässt (wir lassen also Reibungskräfte außen vor): \[ \boldsymbol{F} = - \nabla V(\boldsymbol{x}) \] wobei wir im Folgenden statt \(\nabla V(\boldsymbol{x}\) auch die Schreibweise \[ \nabla V(\boldsymbol{x}) = \frac{d}{d\boldsymbol{x}} V(\boldsymbol{x}) \] verwenden werden. Das Newtonsche Bewegungsgesetz lautet dann \[ m \frac{d^2}{dt^2} \, \boldsymbol{x}(t) = - \nabla V(\boldsymbol{x}) \] Es handelt sich dabei um eine Differentialgleichung zweiter Ordnung für die gesuchte Bahnkurve \(\boldsymbol{x}(t)\) im Potential \(V(\boldsymbol{x})\). Diese Funktion ist eindeutig festgelegt, wenn wir zu einem bestimmten Zeitpunkt (sagen wir, bei \(t = 0\)) den Ort \(\boldsymbol{x}(0)\) und die Geschwindigkeit \( \boldsymbol{v}(0)\) des Objektes vorgeben.
Für den Übergang zur Quantentheorie ist es nützlich, das Newtonsche Bewegungsgesetz aus einem Variationsprinzip herzuleiten. Den Grund dafür werden wir erst verstehen, wenn wir die Quantentheorie konstruiert haben, denn dann ergibt sich der klassische Grenzfall gerade über ein solches Variationsprinzip.
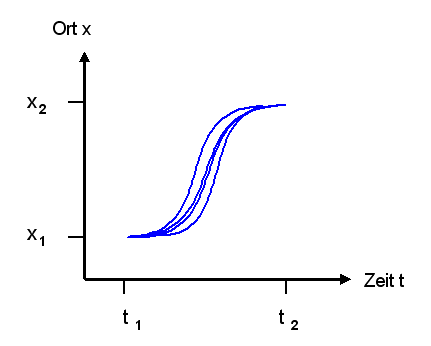
Für die Formulierung als Variationsproblem geben nicht Ort und Geschwindigkeit zu einer Zeit \(t = 0\) vor, sondern wir sagen, dass das Objekt zum Startzeitpunkt Zeit \(t_1\) am Ort \( \boldsymbol{x}_1 = \boldsymbol{x}(t_1) \) sein soll und zu einem späteren Zeitpunkt \(t_1\) am Ort \( \boldsymbol{x}_2 = \boldsymbol{x}(t_2) \). Welche Bahnkurve \(\boldsymbol{x}(t)\) erfüllt diese Bedingungen und genügt dabei zugleich der obigen Differentialgleichung, also dem Bewegungsgesetz von Newton?
Um die Bahnkurve \(\boldsymbol{x}(t)\) zu finden, wollen wir ein Funktional \(S\) konstruieren, das jeder beliebigen (hinreichend glatten) Kurve \(\boldsymbol{x}(t)\), die \( \boldsymbol{x}_1 = \boldsymbol{x}(t_1) \) und \( \boldsymbol{x}_2 = \boldsymbol{x}(t_2) \) erfüllt (aber noch nicht unbedingt dem Bewegungsgesetz von Newton genügen muss), eine reelle Zahl zuordnet.
Man bezeichnet \(S\) als Wirkungsfunktional oder kurz als Wirkung. Die Kurve, die für \(S\) den kleinsten Wert liefert, soll dann die gesuchte Bahnkurve sein und das Bewegungsgesetz von Newton erfüllen. Die in den Punkten \(\boldsymbol{x}_1\) und \(\boldsymbol{x}_2\) fixierte Kurve wird also gleichsam solange verbogen und variiert, bis das Minimum von \(S\) gefunden ist – daher der Begriff Variationsprinzip. Man spricht hier auch vom Prinzip der kleinsten Wirkung oder auch vom Hamiltonschen Prinzip.
Für das Wirkungsfunktional \(S\) machen wir den folgenden Ansatz: \[ S[\boldsymbol{x}] = \int_{t_1}^{t_2} \, L(\boldsymbol{x}(t), \boldsymbol{v}(t)) \, dt \] mit der Geschwindigkeit \( \boldsymbol{v}(t) = d\boldsymbol{x}(t)/dt \).
Die Wirkung jeder potenziellen Bahnkurve \(\boldsymbol{x}\), die unsere Randbedingung \( \boldsymbol{x}_1 = \boldsymbol{x}(t_1) \) und \( \boldsymbol{x}_2 = \boldsymbol{x}(t_2) \) erfüllt, soll also ein Integral über das Zeitintervall von \(t_1\) bis \(t_2\) sein, wobei über eine Funktion \(L\) integriert wird, die als Argument den Ort und die Geschwindigkeit der Kurve zum Zeitpunkt \(t\) enthält. Diese Funktion \(L\) bezeichnet man als Lagrangefunktion. Sie ist bei einem Teilchen im dreidimensionalen Raum und ohne explizite Zeitabhängigkeit also eine Funktion von drei Raumkoordinaten und drei Geschwindigkeitskoordinaten.
Gesucht ist nun die Bahnkurve, für die \(S\) minimal wird. Dazu macht man den Ansatz \[ \boldsymbol{x}(t) = \boldsymbol{x}_0(t) + \epsilon \, \boldsymbol{\eta}(t) \] wobei \( \boldsymbol{x}_0(t) \) die gesuchte Bahnkurve ist und \( \epsilon \, \boldsymbol{\eta}(t) \) die Abweichung von dieser gesuchten Bahnkurve darstellt. Dabei ist \( \boldsymbol{\eta}(t) \) irgendeine (differenzierbare) Funktion, die \( \boldsymbol{\eta}(t_1) = \boldsymbol{\eta}(t_2) = 0 \) erfüllt, damit unsere Randbedingung für alle Kandidatenkurven \(\boldsymbol{x}(t)\) gilt. Der Parameter \(\epsilon\) ist eine reelle Zahl, die steuert, wie weit wir von der gesuchten Kurve abweichen wollen. Analog gilt für die Geschwindigkeit \begin{align} \boldsymbol{v}(t) &= \frac{d}{dt} \boldsymbol{x}(t) = \\ & \\ &= \frac{d}{dt} \boldsymbol{x}_0(t) + \epsilon \, \frac{d}{dt} \boldsymbol{\eta}(t) = \\ & \\ &=: \boldsymbol{v}_0(t) + \epsilon \, \boldsymbol{v}_{\eta}(t) \end{align}

Wir suchen nun das Minimum von \( S[\boldsymbol{x}] \) über die Bedingung \[ \frac{d}{d \epsilon} \, S[\boldsymbol{x}_0 + \epsilon \, \boldsymbol{\eta}] \, \big{|}_{\epsilon = 0} = 0 \] d.h. wir verlangen, dass \(S\) sich in der unmittelbaren Umgebung der gesuchten Kurve erst in der zweiten Ordnung mit \( \epsilon \) ändert, also dort ein Maximum, Minimum oder einen Sattelpunkt hat. Dass es sich um ein Minimum handelt, wollen wir hier nicht näher untersuchen – es ist eigentlich immer so. Man spricht deshalb vom Prinzip der kleinsten Wirkung.
Wie sieht nun die Lagrangefunktion \(L\) aus, sodass wir Newtons Bewegungsgestz aus dem Prinzip der kleinsten Wirkung zurückgewinnen? Um das herauszufinden, können wir die obige Bedingung für \(S\) in eine Differentialgleichung für die Bahnkurve \(\boldsymbol{x}(t)\) übersetzen und dann durch einen Vergleich mit dem Newtonschen Kraftgesetz oben ermitteln, wie die Lagrangefunktion \(L\) aussehen muss: \[ \frac{d}{d \epsilon} \, S[\boldsymbol{x}_0 + \epsilon \, \boldsymbol{\eta}] = \] \[ = \frac{d}{d \epsilon} \, \int_{t_1}^{t_2} \, L(\boldsymbol{x}(t), \boldsymbol{v}(t)) \, dt = \, ... \] ... wir ziehen \( \frac{d}{d \epsilon} \) unter das Zeitintegral: \[ ... \, = \int_{t_1}^{t_2} \, \frac{d}{d \epsilon} \, L(\boldsymbol{x}(t), \boldsymbol{v}(t)) \, dt = \, ... \] ... wir führen d/dε mit Hilfe der Kettenregel aus: \[ ... \, = \int_{t_1}^{t_2} \, \left( \frac{dL}{d\boldsymbol{x}} \, \frac{d\boldsymbol{x}}{d \epsilon} + \frac{dL}{d\boldsymbol{v}} \, \frac{d\boldsymbol{v}}{d \epsilon} \right) \, dt = \, ... \] ... wir verwenden \( \frac{d\boldsymbol{v}}{d \epsilon} = \) \( \frac{d}{d \epsilon} \frac{d\boldsymbol{x}}{dt} = \) \( \frac{d}{dt} \frac{d\boldsymbol{x}}{d \epsilon} \), d.h. wir vertauschen die Reihenfolge der Ableitungen \[ ... \, = \int_{t_1}^{t_2} \, \left( \frac{dL}{d\boldsymbol{x}} \, \frac{d\boldsymbol{x}}{d \epsilon} + \frac{dL}{d\boldsymbol{v}} \, \frac{d}{dt} \frac{d\boldsymbol{x}}{d \epsilon} \right) \, dt = \, ... \] ... der zweite Term wird jetzt partiell integriert: \[ ... \, = \int_{t_1}^{t_2} \, \frac{dL}{d\boldsymbol{x}} \, \frac{d\boldsymbol{x}}{d \epsilon} + \] \[ + \frac{dL}{d\boldsymbol{v}} \, \frac{d\boldsymbol{x}}{d \epsilon} \, \bigg|_{t_1}^{t_2} + \] \[ - \int_{t_1}^{t_2} \, \left( \frac{d}{dt} \frac{dL}{d\boldsymbol{v}} \right) \, \frac{d\boldsymbol{x}}{d \epsilon} \, dt = \, ... \] ... der mittlere Term, der an den beiden Zeitgrenzen ausgewertet wird, ist Null, denn \( \frac{d\boldsymbol{x}}{d \epsilon}(t_2) = \boldsymbol{\eta}(t_2) = 0 \) und analog für \(t_1\): \[ ... \, = \int_{t_1}^{t_2} \, \left( \frac{dL}{d\boldsymbol{x}} \, \frac{d\boldsymbol{x}}{d \epsilon} - \left( \frac{d}{dt} \frac{dL}{d\boldsymbol{v}} \right) \, \frac{d\boldsymbol{x}}{d \epsilon} \right) \, dt = \, ... \] ... jetzt noch \( \frac{d\boldsymbol{x}}{d \epsilon} = \boldsymbol{\eta} \) ausklammern: \[ ... \, = \int_{t_1}^{t_2} \, \left( \frac{dL}{d\boldsymbol{x}} - \left( \frac{d}{dt} \frac{dL}{d\boldsymbol{v}} \right) \right) \, \boldsymbol{\eta}(t) \, dt \] Dieses Integral kann für beliebige Funktionen \(\boldsymbol{\eta}(t)\) nur dann Null sein, wenn der Term in der großen Klammer Null ist, was etwas umgestellt so aussieht \[ \frac{d}{dt} \frac{dL}{d\boldsymbol{v}} = \frac{dL}{d\boldsymbol{x}} \] Das ist die sogenannten Euler-Lagrange-Gleichung für die gesuchte Bahnkurve \(\boldsymbol{x}(t)\), die wir aus dem Prinzip der kleinsten Wirkung (plus Randbedingungen) für diese Bahnkurve abgeleitet haben.
Um die Langrangefunktion \(L\) zu ermitteln, müssen wir die obige Euler-Lagrange-Gleichung mit der Newtonschen Bewegungsgleichung \[ m \frac{d \boldsymbol{v}}{dt} = - \frac{d V(\boldsymbol{x})}{d\boldsymbol{x}} \] vergleichen, die wir diesmal mit der Geschwindigkeit \(\boldsymbol{v}\) ausgedrückt und den Gradienten des Potentials als \(\frac{d V(\boldsymbol{x})}{d\boldsymbol{x}}\) geschrieben haben.
Wenn wir beispielsweise \[ L = \frac{m}{2} \boldsymbol{v}^2 - V(\boldsymbol{x}) \] wählen (also kinetische minus potentielle Energie des Teilchens), so ergibt die Euler-Lagrange-Gleichung gerade die Newtonsche Bewegungsgleichung. Dabei können wir \(L\) natürlich nur bis auf einen Zahlenfaktor festlegen – auch \(2 L\) ginge. Das Vorzeichen von \(L\) ist gerade so gewählt, dass die gesuchte Bahnkurve ein Minimum und kein Maximum von \(S\) ist – die Begründung wollen wir hier überspringen, denn das ist kein besonders wichtiger Punkt. Halten wir fest:
Man kann nun an dieser Stelle bereits zur Quantentheorie übergehen, indem man den Formalismus der Pfadintegrale verwendet – dieser Weg wird daher auch als Lagrange-Zugang zur Quantentheorie bezeichnet. Diese Methode ist besonders bei Eichfeldern sehr nützlich und zeigt sehr schön, was beim Übergang von der klassischen Theorie zur Quantentheorie eigentlich geschieht. Wir werden uns am Ende dieses Kapitels die Details dazu ansehen.
Zunächst jedoch wollen wir den klassischen Hamiltonschen Weg einschlagen, der uns zum oben gesuchten Hamiltonoperator der Quantentheorie führen wird. Dazu müssen wir die klassische Mechanik noch etwas umformulieren, indem wir eine sogenannte Legendre-Transformation durchführen. Was wollen wir damit erreichen?
Die Euler-Lagrange-Gleichung ist eine Differentialgleichung zweiter Ordnung für die gesuchte Bahnkurve \( \boldsymbol{x}(t) \). Für manche Zwecke (z.B. für Symmetriebetrachtungen) ist es jedoch nützlich, stattdessen zwei Differentialgleichungen erster Ordnung zu verwenden. Man kann dies erreichen, indem man z.B. die Geschwindigkeit \( \boldsymbol{v}(t) = d\boldsymbol{x}(t)/dt \) als zweite Funktion neben der Funktion \( \boldsymbol{x}(t) \) betrachtet, die über die obige Gleichung mit \(\boldsymbol{x}(t)\) verknüpft ist. Viel gewonnen hat man jedoch dadurch zunächst nicht.
Schön wäre es, eine Formulierung zu finden, in der die Funktionen \( \boldsymbol{x}(t) \) und eine weitere Funktion ähnlich zu \( \boldsymbol{v}(t) \) möglichst gleichberechtigt vorkommen, wobei aber nicht eine dieser Funktionen einfach nur die zeitliche Ableitung der anderen Funktion ist. Wie können wir das erreichen?
Der Trick ist, statt der Geschwindigkeit die Variable \[ \boldsymbol{p} := \frac{dL}{d\boldsymbol{v}} \] zu verwenden. Setzen wir hier \[ L = \frac{m}{2} \boldsymbol{v}^2 - V(\boldsymbol{x}) \] ein, so ist \[ \boldsymbol{p} = m \boldsymbol{v} \] d.h. es handelt sich um den nichtrelativistischen Impuls des Teilchens. Wir wollen aber im Folgenden den Formalismus weiter allgemein halten, ohne schon jetzt bestimmtes \(L\) zu verwenden, d.h. wir wollen \(\boldsymbol{p} = m \boldsymbol{v}\) nicht voraussetzen, sondern uns auf das allgemeinere \(\boldsymbol{p} := \frac{dL}{d\boldsymbol{v}}\) beziehen.
Dadurch, dass wir statt \(\boldsymbol{v}\) die Variable \(\boldsymbol{p} := \frac{dL}{d\boldsymbol{v}}\) verwenden, liefert die Euler-Lagrange-Gleichung \[ \frac{d}{dt} \frac{dL}{d\boldsymbol{v}} = \frac{dL}{d\boldsymbol{x}} \] unmittelbar die folgende Differentialgleichung erster Ordnung für die gesuchte Funktion \(\boldsymbol{p}(t)\): \[ \frac{d}{dt} \boldsymbol{p} = \frac{dL}{d\boldsymbol{x}} \] In der Lagrangefunktion \(L\) rechts kommt allerdings immer noch die Geschwindigkeit \(\boldsymbol{v}\) vor. Diese können im konkreten Fall loswerden, indem wir die Beziehung \( \boldsymbol{p} := \frac{dL}{d\boldsymbol{v}} \) nach \(\boldsymbol{v}\) freistellen und so \(\boldsymbol{v}\) durch \(\boldsymbol{p}\) ausdrücken. Im obigen Beispiel (nichtrelativistisches Teilchen im Potenzial) ist dann \(\boldsymbol{v} = \boldsymbol{p}/m\).
Es gibt nun einen Trick, mit dem man eine Formalismus erzeugen kann, der \(\boldsymbol{x}\) und \(\boldsymbol{p}\) auf fast gleichwertiger Stufe behandelt. Dazu erzeugt man aus der Lagrangefunktion \(L(\boldsymbol{x}, \boldsymbol{v})\) auf geschickte Weise eine neue Funktion \(H(\boldsymbol{x}, \boldsymbol{p})\), und zwar so, dass man in der Differentialgleichung \( \frac{d}{dt} \boldsymbol{p} = \frac{dL}{d\boldsymbol{x}} \) die rechte Seite in einfacher Weise durch den Term \(\frac{dH}{d\boldsymbol{x}}\) ausdrücken kann.
Außerdem benötigen wir neben der Differentialgleichung für \(\boldsymbol{p}(t)\) noch eine Differentialgleichung für \(\boldsymbol{x}(t)\), die wir auch mit Hilfe der neuen Funktion \(H(\boldsymbol{x}, \boldsymbol{p})\) formulieren wollen. Eine solche Differentialgleichung wäre leicht zu bekommen, wenn man analog zu \[ \boldsymbol{p} := \frac{dL}{d\boldsymbol{v}} \] auch umgekehrt \[ \boldsymbol{v} = \frac{dH}{d\boldsymbol{p}} \] hätte, denn dann wäre wegen \( \boldsymbol{v} = \frac{d}{dt} \boldsymbol{x}\) natürlich sofort \[ \frac{d}{dt} \boldsymbol{x} = \frac{dH}{d\boldsymbol{p}} \] Fassen wir also zusammen:
Natürlich hätten wir diese Forderungen nicht aufgestellt, wenn sie nicht auch erfüllbar wären. Die einfache Funktion \[ H(\boldsymbol{x}, \boldsymbol{p}) := \boldsymbol{p v} - L(\boldsymbol{x}, \boldsymbol{v}) \] erfüllt alle Anforderungen, wie wir gleich nachweisen werden, wobei wir rechts \(\boldsymbol{v}\) als Funktion von \(\boldsymbol{p}\) (und evtl. \(\boldsymbol{x}\)) ausdrücken müssen.
Man bezeichnet \(H\) als Hamiltonfunktion. Die ganze Umformung führt dabei nicht unbedingt zu einer besseren Lösbarkeit der Bewegungsgleichung, sondern man verändert den Blickwinkel, da \(\boldsymbol{x}\) und \(\boldsymbol{p}\) als weitgehend gleichberechtigte Variablen eingehen. Das ermöglicht eine geometrische Interpretation im Raum dieser beiden Variablen, wie wir gleich sehen werden.
Schauen wir uns an, warum diese Hamiltonfunktion \(H\) gerade die gewünschten Eigenschaften hat. Dazu nehmen wir an, dass wir die Argumente von \(L\) und \(H\) über einen reellen Parameter \( \epsilon \) verändern können, z.B. \( \boldsymbol{x} = \boldsymbol{x}_0 + \epsilon \, \boldsymbol{\eta} \) usw. (das kennen wir schon von oben) und betrachten die Veränderung von \(H\) mit \( \epsilon \): \[ \frac{dH}{d\epsilon} = \frac{dH}{d\boldsymbol{x}} \frac{d\boldsymbol{x}}{d\epsilon} + \frac{dH}{d\boldsymbol{p}} \frac{d\boldsymbol{p}}{d\epsilon} \] Andererseits ist wegen \( H(\boldsymbol{x}, \boldsymbol{p}) := \boldsymbol{p v} - L(\boldsymbol{x}, \boldsymbol{v}) \) auch \begin{align} \frac{dH}{d\epsilon} &= \boldsymbol{p} \frac{d\boldsymbol{v}}{d\epsilon} + \boldsymbol{v} \frac{d\boldsymbol{p}}{d\epsilon} - \frac{dL}{d\boldsymbol{x}} \frac{d\boldsymbol{x}}{d\epsilon} - \frac{dL}{d\boldsymbol{v}} \frac{d\boldsymbol{v}}{d\epsilon} = \\ &= \boldsymbol{p} \frac{d\boldsymbol{v}}{d\epsilon} + \boldsymbol{v} \frac{d\boldsymbol{p}}{d\epsilon} - \frac{dL}{d\boldsymbol{x}} \frac{d\boldsymbol{x}}{d\epsilon} - \boldsymbol{p} \frac{d\boldsymbol{v}}{d\epsilon} = \\ &= \boldsymbol{v} \frac{d\boldsymbol{p}}{d\epsilon} - \frac{dL}{d\boldsymbol{x}} \frac{d\boldsymbol{x}}{d\epsilon} \end{align} Vergleicht man diese beiden Gleichungen, dann sieht man, dass \begin{align} \boldsymbol{v} &= \frac{dH}{d\boldsymbol{p}} \\ \frac{dH}{d\boldsymbol{x}} &= - \frac{dL}{d\boldsymbol{x}} \end{align} gelten muss – genauso wie gewünscht! Entscheidend dabei war, dass der Term mit \( \frac{d\boldsymbol{v}}{d\epsilon} \) wegfällt, so dass die Veränderung von \(H\) mit \(\epsilon\) in erster Ordnung nicht von der Veränderung von \(\boldsymbol{v}\) mit \(\epsilon\) abhängt. Man bezeichnet diesen Wechsel von \(\boldsymbol{x}, \boldsymbol{v}\) und \(L(\boldsymbol{x}, \boldsymbol{v})\) zu \(\boldsymbol{x}, \boldsymbol{p}\) und \(H(\boldsymbol{x}, \boldsymbol{p})\) mit \( \boldsymbol{p} := \frac{dL}{d\boldsymbol{v}} \) und \( H = \boldsymbol{p v} - L \) als Legendre-Transformation .
Die Legendre-Transformation kann durch nochmaliges Ausführen wieder rückgängig gemacht werden: setze \( L := \boldsymbol{p v} - H \) und \(\boldsymbol{v} := \frac{dH}{d\boldsymbol{p}}\), um die ursprüngliche Lagrange-Funktion \(L\) und die ursprüngliche Variable \(\boldsymbol{v}\) wieder zurückzuerhalten. Dies macht die Legendre-Transformation auch für andere Zusammenhänge (z.B. für die thermodynamischen Potentiale) sehr nützlich.
Mit Hilfe der Legendre-Transformation ist es nun gelungen, die ursprüngliche Aufgabe (löse die Euler-Lagrange-Differentialgleichung zweiter Ordnung für die Funktion \(\boldsymbol{x}(t)\)) in eine neue Aufgabe umzuformulieren:
Was hat man durch diese Umformulierung gewonnen?
Man hat eine Formulierung erhalten, in der gleichberechtigt zwei Funktionen \(\boldsymbol{x}(t)\) und \(\boldsymbol{p}(t)\) vorkommen, die zwei sehr ähnliche Differentialgleichungen erster Ordnung erfüllen müssen. Man kann nun diese Formulierung der Mechanik in eine geometrische Sprache übersetzen und sie so den Werkzeugen der Differentialgeometrie zugänglich machen. Dazu fasst man die Koordinaten \(\boldsymbol{x}\) und \(\boldsymbol{p}\) zu einem Vektor zusammen: \((\boldsymbol{x}, \boldsymbol{p})\). Der Raum dieser Vektoren hat also eine doppelt so große Dimension wie der \(\boldsymbol{x}\)-Raum alleine, ist also im Fall eines Teilchens 6-dimensional. Man bezeichnet diesen Raum als Phasenraum. Die Bewegung des Teilchens wird nun durch eine Kurve \((\boldsymbol{x}(t), \boldsymbol{p}(t))\) in diesem Phasenraum dargestellt.
Um die Bewegungsgleichungen zu lösen, kann man nun versuchen, in diesem Phasenraum nach neuen geeigneten Koordinaten zu suchen, so dass die Bewegungsgleichungen eine möglichst einfache Form erhalten. Dabei können Orts- und Impulskoordinaten auch miteinander zu neuen Koordinaten kombiniert werden, d.h. diese Methode geht über angepasste Ortskoordinaten (z.B. Polarkoordinaten) hinaus. Darin liegt einer der Vorteile der neuen Formulierung mit Hilfe der Hamiltonfunktion \(H\).
Um die Tragweite der Hamiltonschen Formulierung der Mechanik besser zu erkennen, ist es nützlich, die Auswirkung der oben genannten Hamiltonschen Differentialgleichungen mit Hilfe des Phasenraums in eine geometrische Sprache zu übersetzen.
Schauen wir uns irgendeine Funktion \(f(\boldsymbol{x}, \boldsymbol{p})\) an, die im Phasenraum definiert ist. Wie verändert sich \(f\) zeitlich entlang der Bahnkurve \((\boldsymbol{x}(t), \boldsymbol{p}(t))\), d.h. wie verändert sich \(f\) im Verlauf der Bewegung des Teilchens? Rechnen wir es unter Verwendung der Hamiltonschen Bewegungsgleichung aus: \begin{align} & \frac{d}{dt} f(\boldsymbol{x}(t), \boldsymbol{p}(t)) = \\ & \\ &= \frac{df}{d\boldsymbol{x}} \frac{d\boldsymbol{x}}{dt} + \frac{df}{d\boldsymbol{p}} \frac{d\boldsymbol{p}}{dt} = \\ & \\ &= \frac{df}{d\boldsymbol{x}} \frac{dH}{d\boldsymbol{p}} - \frac{df}{d\boldsymbol{p}} \frac{dH}{d\boldsymbol{x}} = \\ & \\ &=: \{ H, f \} \end{align} wobei wir zur Vereinfachung der Schreibweise oben die Poissonklammer \[ \{ H, f \} = \frac{df}{d\boldsymbol{x}} \frac{dH}{d\boldsymbol{p}} - \frac{df}{d\boldsymbol{p}} \frac{dH}{d\boldsymbol{x}} \] für Funktionen im Phasenraum einführen. Die Schreibweise bedeutet, dass komponentenweise multipliziert und anschließend über die Komponenten summiert wird, also wie beim gewöhnlichen Skalarprodukt dreidimensionaler reeller Vektoren. Weiter gilt \( \{ H, f \} = - \{ f, H \} \), d.h. die Poissonklammer ist antisymmetrisch.
Die Poissonklammer hat eine einfache anschauliche Bedeutung: Sie ist im Phasenraum die Richtungsableitung der Funktion \(f\) entlang der Höhenlinien von \(H\) (also entlang der Linien mit konstantem \(H\)). \( \{ H, f \} \) misst also, wie schnell sich \(f\) ändert, wenn man sich im Phasenraum entlang der Höhenlinien von \(H\) bewegt. Dies ist auch gleichzeitig die zeitliche Änderung von \(f\) entlang der Bahnkurve \( (\boldsymbol{x}(t), \boldsymbol{p}(t)) \). Das kann man auch anschaulich verstehen, wenn man sich klarmacht, dass die Bahnkurve im Phasenraum entlang der Höhenlinien von \(H\) verläuft, d.h. \(H\) ist eine Konstante der Bewegung (wir setzen voraus, dass \(H\) und \(f\) nicht explizit zeitabhängig sind). Setzen wir nämlich \(f = H\) ein, so ist \( dH/dt = \{H, H\} = 0 \).
Wie sieht \(H\) bei einem Teilchen in einem klassischen Potential aus? Für ein solches Teilchen war \[ L = \frac{m}{2} \boldsymbol{v}^2 - V(\boldsymbol{x}) \] (siehe oben). Dann ist \[ \boldsymbol{p} = \frac{dL}{d\boldsymbol{v}} = m \boldsymbol{v} \] und somit \begin{align} H &= \boldsymbol{p v} - L = \\ & \\ &= \boldsymbol{p} \frac{\boldsymbol{p}}{m} - \frac{m}{2} \frac{\boldsymbol{p}^2}{m^2} + V(\boldsymbol{x}) = \\ & \\ &= \frac{\boldsymbol{p}^2}{2m} + V(\boldsymbol{x}) \end{align} d.h. \(H\) ist die Summe aus kinetischer plus potentieller Energie. Die Hamiltonfunktion ist also als die Gesamtenergie des Teilchens zu interpretieren. Kein Wunder, dass sie in einem konservativen Kraftfeld konstant ist. Übrigens hebt diese spezielle Form von \(H\) die Gleichberechtigung der beiden Variablen \(\boldsymbol{x}\) und \(\boldsymbol{p}\) wieder ein Stück weit auf, denn \(\boldsymbol{p}\) kommt darin garantiert quadratisch vor, \(\boldsymbol{x}\) dagegen nicht unbedingt – man denke an Potentiale wie \(V(\boldsymbol{x}) = k/|\boldsymbol{x}|\). Nur beim harmonischen Oszillator mit \(V(\boldsymbol{x}) = k \boldsymbol{x}^2\) sind beide Variablen wirklich gleichberechtigt – deshalb ist er in der Physik und besonders in der Quantenmechanik auch so beliebt!
Nun sind wir gerüstet, um den Übergang zur Quantentheorie zu versuchen. Dabei wollen wir zunächst den Weg gehen, der auf der gerade besprochenen Hamiltonschen Formulierung der klassischen Mechanik beruht. Diesen Weg bezeichnet man auch als kanonische Quantisierung.
Im ersten Schritt müssen wir dazu die relevanten dynamischen Variablen der klassischen Theorie identifizieren. In der Hamiltonschen Formulierung der Mechanik sind dies der Ort \(\boldsymbol{x}\) und der dazu kanonisch konjugierte Impuls \( \boldsymbol{p} := \frac{dL}{d\boldsymbol{v}} \) des Teilchens (wir beschränken uns wieder auf ein Teilchen in einem äußeren Potential; die Verallgemeinerung auf mehrere Teilchen ist nicht schwer, verkompliziert die Diskussion aber hier nur unnötig). Diesen dynamischen Variablen ordnen wir in der Quantentheorie nun gewisse Operatoren zu, die auf die Zustandsvektoren einwirken und diese verändern können. Um die Schreibweise einfach zu halten, wollen wir den quantenmechanischen Orts- und Impulsoperator mit den Buchstaben \(\boldsymbol{\hat{x}}\) und \(\boldsymbol{\hat{p}}\) bezeichnen, also mit Hut oben drauf. Der Fettdruck deutet wieder an, dass es sich um Vektoren handelt, also um einen Operator für jede Vektorkomponente. Diese Operatoren bilden die dynamische Grundlage unserer Quantentheorie. Alle anderen Operatoren werden aus ihnen aufgebaut.
Als nächstes müssen wir uns um beobachtbare Größen kümmern. Im Fall der nichtrelativistischen Mechanik sind in der zugehörigen Quantentheorie Ort und Impuls selbst bereits beobachtbare Größen, d.h. Orts- und Impulsoperator sind hermitesche Operatoren.
Allgemein sind in der klassischen Hamiltonschen Mechanik beobachtbare Größen Funktionen von Ort und Impuls, also Funktionen auf dem Phasenraum. In der Quantentheorie dagegen müssen diese beobachtbaren Größen durch hermitesche Operatoren dargestellt werden. Diese Operatoren sollen mit Hilfe der Operatoren \(\boldsymbol{\hat{x}}\) und \(\boldsymbol{\hat{p}}\) aufgebaut werden. Aber wie?
Betrachten wir als Beispiel die kinetische Energie \( \frac{\boldsymbol{p}^2}{2m} \). Wie sieht der entsprechende Operator in der Quantentheorie aus?
Um dies festlegen zu können, müssen wir den Übergang von der Quantentheorie zur klassischen Theorie betrachten. Was bedeutet dieser Übergang?
Der klassische Grenzfall einer Quantentheorie bedeutet, dass bei vielen Messungen an identischen Quantensystemen die Messwerte nur noch sehr wenig um den Mittelwert (Erwartungswert) aller Messungen schwanken. Es kommt praktisch immer derselbe Messwert heraus, d.h. Erwartungswerte gehen in die klassischen Funktionswerte über. Genau dies ist die Charakterisierung des klassischen Grenzfalls: aus Erwartungswerten werden die klassischen Funktionswerte.
Nehmen wir nun an, dass zur kinetischen Energie in der Quantentheorie der Operator \( \frac{1}{2m} \boldsymbol{\hat{p}}^2 \) gehört. Im klassischen Grenzfall können wir also den quantenmechanischen Erwartungswert der kinetischen Energie \[ \frac{1}{2m} \langle \psi(t) | \, \boldsymbol{\hat{p}}^2 \psi(t) \rangle \] durch den Ausdruck \[ \frac{1}{2m} \langle \psi(t) | \, \boldsymbol{\hat{p}} \, \psi(t) \rangle^2 \] ersetzen, da die Streuung der Messwerte sehr klein ist. Der Erwartungswert \( \langle \psi(t) | \, \boldsymbol{\hat{p}} \, \psi(t) \rangle \) wird aber im klassischen Grenzfall gleich der klassischen Funktion \( \boldsymbol{p}(t) \), d.h. der Erwartungswert der kinetischen Energie wird gleich der klassischen kinetischen Energie \( \frac{\boldsymbol{p}(t)^2}{2m} \).
Allgemein wird im klassischen Grenzfall aus dem Erwartungswert eines Produktes von hermiteschen Operatoren das Produkt der Erwartungswerte dieser Operatoren. Wenn wir also einem Polynom aus den klassischen Größen \( \boldsymbol{x}(t) \) und \( \boldsymbol{p}(t) \) beim Übergang zur Quantenmechanik das entsprechende Polynom der Operatoren zuordnen, so ist sichergestellt, dass im klassischen Grenzfall der Erwartungswert dieses Operators in das Produkt der klassischen Größen übergeht.
Wir werden generell versuchen, den quantenmechanischen Operator zu einer klassischen Funktion genau so aus den Operatoren \(\boldsymbol{\hat{x}}\) und \(\boldsymbol{\hat{p}}\) aufzubauen, wie diese klassische Funktion aus den Variablen \( \boldsymbol{x} \) und \( \boldsymbol{p} \) aufgebaut ist. Eine Rechtfertigung für diese Vorgehensweise haben wir immer dann, wenn man die klassische Funktion in eine Potenzreihe entwickeln kann und dann Terme wie \( \boldsymbol{\hat{p}}^2 \) als zweifaches Anwenden des Impulsoperators versteht.
Kompliziert wird die Angelegenheit aber, wenn Terme wie \( \boldsymbol{x p} \) auftreten. Soll man daraus den Operator \( \boldsymbol{\hat{x} \hat{p}} \) oder den Operator \( \boldsymbol{\hat{p} \hat{x}} \) machen? Das muss keineswegs derselbe Operator sein, wie wir noch sehen werden.
Der Übergang von klassischen Funktionen des Phasenraums zu hermiteschen Operatoren der Quantentheorie ist also nicht unbedingt eindeutig, und man muss gegebenenfalls Zusatzüberlegungen anstellen, um eine geeignete Quantisierung einer klassischen Theorie zu formulieren. Wir sehen also: Die Quantisierung einer klassischen Theorie ist kein geradliniger und komplikationsfreier Prozess, sondern man muss Zusatzinformationen hineinstecken, die die klassische Theorie nicht enthält. Das ist auch nicht so überaschend, denn schließlich geht die Quantentheorie ja über die klassische Nicht-Quantentheorie hinaus, und es gibt lediglich die Randbedingung, dass die klassische Theorie sich als Grenzfall der Quantentheorie ergibt (d.h. aus Erwartungswerten hermitescher Operatoren müssen dann die klassischen beobachtbaren Größen werden).
Kommen wir nun zum Hamiltonoperator:
Nach dem gerade Gesagten sieht der quantenmechanische Hamiltonoperator für ein nichtrelativistisches freies Teilchen in einem äußeren Potential genauso aus wie die klassische Hamiltonfunktion, nur mit dem Impulsoperator statt dem klassischen Teilchenimpuls und dem Ortsoperator statt dem klassischen Teilchenort: \[ H = \frac{\boldsymbol{\hat{p}}^2}{2m} + V(\boldsymbol{\hat{x}}) \] Wie \(V(\boldsymbol{\hat{x}})\) zu verstehen ist, müssen wir dabei ggf. noch sehen. Allerdings können wir mit dieser Information noch nicht allzu viel anfangen, denn wir wissen nicht, was die Operatoren \(\boldsymbol{\hat{p}}\) und \(\boldsymbol{\hat{x}}\) im Hilbertraum bewirken. Dazu benötigen noch eine Regel, die festlegt, wie sich die zeitliche Dynamik der klassischen Theorie auf die Quantentheorie überträgt. Diese Regel kennen wir bereits aus dem vorhergehenden Kapitel: es ist die Schrödingergleichung \[ i \hbar \frac{d}{dt} | \psi (t) \rangle = H \, | \psi (t) \rangle \] die Zeitentwicklung der Zustandsvektoren bewirkt.
Schauen wir an, was das in der Quantentheorie für die zeitliche Entwicklung von Erwartungswerten (Mittelwerte vieler Messungen) bedeutet. Mit \(A\) wollen wir den hermiteschen Operator zu irgendeiner messbaren Größe bezeichnen, und mit \( | \psi (t) \rangle \) bezeichnen wir wieder den Zustandsvektor, der den Zustand des quantenmechanischen Systems zur Zeit \(t\) beschreibt. \(A\) selbst ist dabei nicht zeitabhängig, d.h. die gesamte Zeitentwicklung steckt in der Veränderung der Zustandsvektoren, die durch die Schrödingergleichung gegeben ist. Damit folgt für die Zeitentwicklung des Erwartungswertes von \(A\): \[ i \hbar \frac{d}{dt} \langle \psi (t) | \, A \, \psi (t) \rangle = \] ... wir verwenden die Produktregel, müssen also \(\psi (t)\) links und rechts nach der Zeit ableiten, wobei sich ein Minuszeichen ergibt, wenn wir \(i\) links in das komplexe Skalarprodukt hineinziehen (denn komplexe Zahlen werden immer komplex konjugiert aus dem linken Teil herausgezogen, wie die Formel \( \langle \phi | \psi \rangle = \int \phi^*(\boldsymbol{x}) \, \psi(\boldsymbol{x}) \, d^3x \) aus dem letzten Kapitel zeigt): \[ = \langle (- i \hbar) \frac{d}{dt} \psi (t) | \, A \, \psi (t) \rangle + \] \[ + \langle \psi (t) | \, A \, i \hbar \frac{d}{dt} \psi (t) \rangle = \] ... wir verwenden die Schrödingergleichung: \[ = - \langle H \psi (t) | \, A \, \psi (t) \rangle + \langle \psi (t) | \, A \, H \psi (t) \rangle = \] ... da \(H\) hermitesch ist, dürfen wir ihn im ersten Term auf die rechte Seite ziehen: \[ = - \langle \psi (t) | \, H \, A \, \psi (t) \rangle + \langle \psi (t) | \, A \, H \psi (t) \rangle = \] ... da die Skalarprodukte linear sind, können wir sie vereinen, wobei wir noch ein Minuszeichen herausziehen: \[ = - \langle \psi (t) | \, (H A - A H) \, \psi (t) \rangle = \] \[ =: - \langle \psi (t) | \, [H, A] \, \psi (t) \rangle \] wobei wir als abkürzende Schreibweise den Kommutator \[ [H, A] := H A - A H \] der beiden Operatoren eingeführt haben. Wenn wir jetzt noch \( i \hbar \) auf die andere Seite bringen (mit \(1/i = -i\), dann erhalten wir: \[ \frac{d}{dt} \langle \psi (t) | \, A \, \psi (t) \rangle = \frac{i}{\hbar} \, \langle \psi (t) | \, [H, A] \, \psi (t) \rangle \] Was bedeutet dieses Ergebnis für den Grenzfall, bei dem die Quantenmechanik in die klassische Mechanik übergeht? Im klassischen Grenzfall sollte die statistische Streuung der Messergebnisse der beobachtbaren Größe gegenüber dem Mittelwert selbst kaum noch ins Gewicht fallen. Jede Messung zur Zeit \(t\) liefert daher ungefähr den Mittelwert, d.h. der Mittelwert wird zum klassisch beobachteten Messwert, der durch die Phasenraum-Funktion \[ A(\boldsymbol{x}(t),\boldsymbol{p}(t)) =: A(t) \] gegeben ist (Vorsicht: wir verwenden dieselbe Schreibweise für die Phasenraum-Funktion \(A(t)\) wie für den Operator \(A\)). Aus \( \frac{d}{dt} \langle \psi (t) | \, A \, \psi (t) \rangle \) wird also im klassischen Grenzfall \( \frac{d}{dt} A(t) \). Für diese zeitliche Ableitung galt in der Hamiltonschen Mechanik (siehe oben mit \( f(t) = A(t) \) ): \[ \frac{d}{dt} A(t) = \{ H, A(t) \} \] mit der weiter oben definierten Poissonklammer. Der quantenmechanische Erwartungswert \[ \frac{i}{\hbar} \, \langle \psi (t) | \, [H, A] \, \psi (t) \rangle \] geht also im klassischen Grenzfall in die Poissonklammer \[ \{ H, A(t) \} \] der klassischen Phasenraum-Funktionen \(H\) und \(A(t)\) über. Daher fordert man umgekehrt, dass beim Übergang von klassischen Phasenraum-Funktionen zu quantenmechanischen Operatoren die Poissonklammern in die entsprechenden Kommutatoren übergehen.
Damit ist auch klar, dass der zur Hamiltonfunktion \(H\) konstruierte Hamiltonoperator \(H\) tatsächlich für die Zeitentwicklung in der Quantentheorie verantwortlich ist, denn dieses Rezept stellt sicher, dass Erwartungswerte sich im klassischen Grenzfall zeitlich wie die entsprechenden Phasenraum-Funktionen entwickeln. Außerdem passt auch mathematisch alles zusammen, denn Kommutatoren haben dieselben algebraischen Eigenschaften wie Poissonklammern, sidn also beispielsweise antisymmetrisch. Halten wir also fest:
Man kann also die Quantisierung einer klassischen Theorie so verstehen: Suche einen Hilbertraum, auf dem man zu jeder klassischen Phasenraumfunktion einen analog aufgebauten Operator definieren kann, so dass Poissonklammern der klassischen Phasenraumfunktionen in Kommutatoren der zugehörigen Operatoren übergehen. Besonders wichtig sind natürlich die Poissonklammern der zugrundeliegenden dynamischen Variablen (hier Ort und Impuls) sowie die Kommutatoren der entsprechenden Operatoren. Wir wollen sie daher noch einmal auflisten:
Für die grundlegenden Poissonklammern rechnet man direkt nach: \begin{align} \{ \boldsymbol{p}, \boldsymbol{x} \} &= 1 \\ \{ \boldsymbol{x}, \boldsymbol{x} \} &= 0 \\ \{ \boldsymbol{p}, \boldsymbol{p} \} &= 0 \end{align} (diese Ausdrücke sind komponentenweise zu lesen: sie gelten separat für alle drei Komponenten der Vektoren \(\boldsymbol{p}\) und \(\boldsymbol{x}\), d.h. \(\{p_i, x_j\} = 1\) nur für \(i = j\) und \(= 0\) für \(i \ne j\)). Diese Poissonklammern müssen nach unserer obigen Quantisierungsregel durch folgende Kommutatoren ersetzt werden (den Faktor \(i/\hbar\) haben wir dabei auf die andere Seite gebracht): \begin{align} [ \boldsymbol{\hat{p}}, \boldsymbol{\hat{x}} ] &= \frac{\hbar}{i} \\ [ \boldsymbol{\hat{x}}, \boldsymbol{\hat{x}} ] &= 0 \\ [ \boldsymbol{\hat{p}}, \boldsymbol{\hat{p}} ] &= 0 \end{align} (diese Kommutatoren sind wie die Poissonklammer komponentenweise zu lesen).
Das ganze Konzept mutet manchmal etwas wie Zauberei an, und es ist ja auch keine absolut strenge Vorgehensweise, sondern eher ein halbwegs systematisches Suchen nach einer Quantentheorie, die im klassischen Grenzfall in eine vorgegebene klassische Theorie übergeht. Dabei kann es immer wieder Überaschungen geben, die man aufgrund der klassischen Theorie nicht bereits vorher erkennen kann. So können Zusatzforderungen nach Kausalität oder nach mathematischer Konsistenz sowie Symmetriebetrachtungen zu weiteren Erkenntnissen führen, wie die Quantentheorie aufgebaut werden muss. Man muss immer wieder überlegen, was man da eigentlich tut, denn das ganze Vorgehen läuft nicht vollautomatisch ab.
Auch wir wollen uns noch einige Gedanken machen, um ein besseres Gefühl für den Vorgang der Quantisierung zu bekommen.
Man kann sich beispielweise fragen, wie der Faktor \(\frac{i}{\hbar}\) zu erklären ist, der beim Übergang von der Poissonklammer zum Kommutator auftritt. Warum dieser Faktor notwendig ist, wird deutlich, wenn wir uns die daraus folgende Zeitentwicklungsgleichung für Erwartungswerte \[ \frac{d}{dt} \langle \psi (t) | \, A \, \psi (t) \rangle = \frac{i}{\hbar} \, \langle \psi (t) | \, [H, A] \, \psi (t) \rangle \] (siehe oben) ansehen. Auf der rechten Seite steht der Erwartungswert eines Kommutators. Was passiert mit diesem Erwartungswert im klassischen Grenzfall?
Oben hatten wir bereits gesagt: Allgemein wird im klassischen Grenzfall aus dem Erwartungswert eines Produktes von hermiteschen Operatoren das Produkt der Erwartungswerte dieser Operatoren. Das bedeutet, dass der Erwartungswert des Kommutators auf der rechten Seite im klassischen Grenzfall gegen Null geht, denn \[ \; \; \; \; \langle \psi | \, H \, \psi \rangle \, \langle \psi | \, A \, \psi \rangle + \] \[ - \langle \psi | \, A \, \psi \rangle \, \langle \psi | \, H \, \psi \rangle \] \[ = 0 \] (das Argument \(t\) lassen wir zur besseren Lesbarkeit weg). Das aber würde bedeuten, dass im klassischen Grenzfall auch \( \frac{d}{dt} \langle \psi | \, A \, \psi \rangle \) gleich Null würde, d.h. es gäbe keine zeitliche Veränderung von Erwartungswerten mehr und damit keine zeitliche Entwicklung der zugehörigen klassischen Größen, in die die Erwartungswerte im klassischen Grenzfall ja übergehen. Das aber kann nicht sein. Was stimmt an dieser Überlegung nicht?
Der Fehler liegt darin, dass die Ausage "allgemein wird im klassischen Grenzfall aus dem Erwartungswert eines Produktes von hermiteschen Operatoren das Produkt der Erwartungswerte dieser Operatoren" nicht genau genug ist, um in diesem Fall den klassischen Grenzfall korrekt zu betrachten. Schauen wir uns daher einmal genauer Erwartungswerte von Kommutatoren an und versuchen, eine anschauliche Vorstellung von ihrer Bedeutung zu gewinnen.
Bei einer großen Zahl von Messungen einer beobachtbaren Größe
(mit zugehörigem Operator \(A\)) bei einem quantenmechanischen System
im Zustand \( | \psi(t) \rangle \)
ist die sogenannte
statistische Standardabweichung (nennen wir sie \(\Delta A\)) so definiert:
Für jeden Messwert bilden wir die Differenz zum Mittelwert aller Messwerte,
quadrieren diese Differenz, bilden den Mittelwert dieser quadrierten Differenzen
und ziehen am Schluss die Wurzel:
\begin{align}
\Delta A
&= \sqrt{ \langle \psi | \, (A - \langle \psi | \, A \, \psi \rangle)^2 \, \psi \rangle } = \\
&= \sqrt{ \langle \psi | \, A^2 \, \psi \rangle - \langle \psi | \, A \, \psi \rangle^2 }
\end{align}
\(\Delta A\) ist also die Wurzel aus der durchschnittlichen quadratischen Abweichung vom Mittelwert.
Eine Standardrechnung (siehe
Wikipedia: Heisenbergsche Unschärferelation –Beweis der verallgemeinerten Unschärferelation)
liefert die Beziehung
\[
\Delta A \cdot \Delta B \ge
\frac{1}{2} \, |\langle \psi | [A, B] \psi \rangle|
\]
Der Erwartungswert des Kommutators von \(A\) und \(B\) liefert also
eine untere Grenze für die multiplizierten Standardabweichungen (die Unschärfen)
der Messwerte von \(A\) und \(B\). Wenn also der Kommutator von \(A\) und \(B\) ungleich Null ist
(d.h. wenn die Operatoren \(A\) und \(B\) nicht miteinander vertauschbar sind),
so streuen die Messwerte von \(A\) oder die von \(B\) (oder beide) um ihren Mittelwert.
Dabei ist die Streuung dieser Messwerte beispielsweise für \(A\) umso größer, je kleiner die
Streuung von \(B\) ist (und umgekehrt).
Man kann also keinen Zustand für das quantenmechanische System präparieren,
in dem sowohl der Messwert von \(A\) als auch der von \(B\) beide immer denselben
scharfen Wert besitzen.
Man bezeichnet dies als die Heisenbergsche Unschärferelation.

Quelle:
Wikimedia Commons File:Werner Heisenberg Briefmarke.jpg,
Briefmarke der Deutschen Post (2001)
Ein Spezialfall dieser Beziehung ist \(A = \hat{p}_j\) und \(B = \hat{x}_j\) (dabei gibt \(j = 1, 2, 3\) die j-te Komponente des Operator-Vektors an). Wegen \[ [ \hat{p}_j, \hat{x}_j ] = \frac{\hbar}{i} \] und der Normierung \( \langle \psi | \psi \rangle = 1 \) folgt \[ \Delta p_j \cdot \Delta x_j \ge \frac{\hbar}{2} \] Oft bezeichnet man auch nur diesen Spezialfall als Heisenbergsche Unschärferelation.
Ein anderer interessanter Spezialfall ist \(A = H\). Nennen wir \(\Delta H\) in das sprechendere \(\Delta E\) um (denn \(\Delta H\) ist ja die Standardabweichung der Energiemesswerte) und verwenden \[ \frac{d}{dt} \langle \psi | \, B \, \psi \rangle = \frac{i}{\hbar} \, \langle \psi | \, [H, B] \, \psi \rangle \] so ist \begin{align} \Delta E \cdot \Delta B &\ge \frac{1}{2} \, |\langle \psi | \, [H, B] \, \psi \rangle| = \\ & \\ &= \frac{\hbar}{2} \, \frac{d}{dt} \, |\langle \psi | \, B \, \psi \rangle| \end{align} Was sagt uns diese Gleichung? Dazu wollen wir eine grobe Abschätzung des rechten Terms vornehmen und \[ \frac{d}{dt} \, |\langle \psi | \, B \, \psi \rangle| \approx \frac{\Delta B}{\Delta t} \] setzen. Die rechte Seite bedeutet: Bei den vielen Messungen schwankt der genaue Messzeitpunkt mit einer Unsicherheit \(\Delta t\). Dies bewirkt eine Unsicherheit \(\Delta B\) in den Messwerten von \(B\), da sich der Mittelwert der Messwerte zeitlich ändert. Setzen wir dies oben ein, so erhalten wir \[ \Delta E \cdot \Delta B \ge \frac{\hbar}{2} \, \frac{\Delta B}{\Delta t} \] Wir wollen grob annehmen, dass die Messwertstreung \(\Delta B\) auf der linken Seite etwa genauso groß ist wie auf der rechten Seite, d.h. wir können \(\Delta B\) wegkürzen und \(\Delta t\) auf die linke Seite bringen: \[ \Delta E \cdot \Delta t \ge \frac{\hbar}{2} \] Diese Ungleichung ist als grobe Abschätzung zu verstehen, d.h. sie lässt sich nicht so präzise begründen wie die Unschärferelation zwischen Ort und Impuls. Dennoch liefert sie zumindest einen Hinweis auf eine Regel, die man näherungsweise immer wieder bestätigt findet:
Zurück zu unserer Frage: wie ist der Faktor \( \frac{i}{\hbar} \) in unserem Kochrezept zur Konstruktion von Quantentheorien zu erklären, der beim Übergang von der Poissonklammer zum Kommutator auftritt? Dazu hatten wir uns die Zeitentwicklung \[ \frac{d}{dt} \langle \psi | \, A \, \psi \rangle = \frac{i}{\hbar} \, \langle \psi | \, [H, A] \, \psi \rangle \] angesehen. Die obigen Überlegungen haben gezeigt, dass der Erwartungswert des Kommutators rechts von der Größenordnung her dem Produkt der Unsicherheiten \( \Delta E \cdot \Delta B \) entspricht. Die obigen Beispiele haben gezeigt, dass dieses Produkt typischerweise etwa die Größenordnung des Planckschen Wirkungsquantums \(h\) (oder \(\hbar\)) aufweist. Den klassischen Grenzfall können wir nun genauer beschreiben: Er entspricht dem Grenzfall, das \(h\) gegen Null geht (d.h. Terme ohne \(h\) dominieren gegenüber Termen, die proportional zu \(h\) sind):
Damit verbunden ist, dass auch die Unsicherheiten von Messwerten klein werden sollten (vorausgesetzt, sie haben vergleichbare Größenordnungen, so dass aus einem kleinen Produkt auch kleine Faktoren folgen). Die Details des klassischen Grenzfalls wirklich sauber aufzustellen erfordert jedoch deutlich mehr Präzision, denn schließlich gibt es auch makroskopische Quantenphänomene (z.B. Supraleitung). So muss man den Begriff der Kohärenz und Dekohärenz mit einbeziehen. Wir wollen hier darauf verzichten.
Mit diesem Verständnis des klassischen Grenzfalls können wir nun sehen, wozu \(h\) (bzw. \(\hbar\)) im Nenner oben benötigt wird: da der Erwartungswert des Kommutators selbst die Größenordnung \(h\) besitzt, sorgt das \(h\) im Nenner dafür, dass beim Grenzübergang \(h\) gegen Null die rechte Seite nicht automatisch gleich Null wird. Nur so kann eine Zeitentwicklung der beobachtbaren Größen links im klasssichen Grenzfall erhalten bleiben.
Einen weiteren Punkt wollen wir uns näher ansehen: Erhalten wir im klassischen Grenzfall die Hamiltonschen Bewegungsgleichungen zurück?
Schauen wir uns den Kommutator \[ \frac{i}{\hbar} \, [H, A] = - \frac{i}{\hbar} \, [A, H] \] für den Spezialfall \(A = \hat{x}\) an (der andere Fall \(A = \hat{p}\) geht analog), also \[ \frac{i}{\hbar} \, [H, \hat{x}] = - \frac{i}{\hbar} \, [\hat{x}, H] \] wobei wir uns hier auf eine Raumdimension beschränken wollen, sodass wir den Raumindex weglassen können. Dabei wollen wir voraussetzen, dass wir \(H\) als Potenzreihe der Operatoren \(\hat{p}\) und \(\hat{x}\) schreiben können.
Terme mit Potenzen von \(\hat{x}\) fallen weg, denn \( [\hat{x}, \hat{x}^n] = 0\).
Terme mit Potenzen von \(\hat{p}\) fallen dagegen nicht weg: \[ \quad [\hat{x}, \hat{p}^{n+1}] = \] \[ = [\hat{x}, \hat{p}^n \hat{p} ] = \] \[ = \hat{x} \hat{p}^n \hat{p} - \hat{p}^n \hat{p} \hat{x} = \] \[ = \hat{x} \hat{p}^n \hat{p} - \hat{p}^n \hat{x} \hat{p} + \hat{p}^n \hat{x} \hat{p} - \hat{p}^n \hat{p} \hat{x} = \] \[ = [\hat{x}, \hat{p}^n] \hat{p} + \hat{p}^n [\hat{x}, \hat{p}] = \] \[ = [\hat{x}, \hat{p}^n] \hat{p} + i \hbar \hat{p}^n \] also insgesamt \[ -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^{n+1} ] = -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^n] \hat{p} + \hat{p}^n \] Mit dem Kommutator \( -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^n] \) auf der rechten Seite können wir nun analog verfahren, so dass \[ -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^{n+1} ] = \] \[ = -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^n] \hat{p} + \hat{p}^n = \] \[ = \left( -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^{n-1}] \hat{p} + \hat{p}^{n-1} \right) \hat{p} + \hat{p}^n = \] \[ = -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^{n-1}] \, \hat{p}^2 + 2 \hat{p}^n \] wird. Das Schema ist klar: der Exponent im Kommutator wird heruntergezählt, und dafür taucht ein weiterer Summand \(\hat{p}^n\) sowie ein weiterer Faktor \(\hat{p}\) auf. Insgesamt können wir in \(n + 1\) Schritten den Exponenten von \(n + 1\) bis auf \(0\) herunterzählen. Der letzte Kommutator \( [\hat{x} , \hat{p}^0]\) ist gleich Null und trägt nicht mehr bei. Daher haben wir insgesamt \[ -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^{n+1} ] = (n+1) \, \hat{p}^{n} \] oder anders geschrieben \[ -\frac{i}{\hbar} \, [\hat{x}, \hat{p}^{n} ] = n \, \hat{p}^{n-1} \] \[ =: \frac{d}{d\hat{p}} \hat{p}^n \] Dabei haben wir den Term \( \frac{d}{d\hat{p}} \hat{p}^n \) (hier ist \(\hat{p}\) ein Operator!) analog zu den Regeln der üblichen Ableitung definiert.
Diese Beziehung gilt für jedes \(n\) und somit für alle \(\hat{p}^n\)-Terme in \(H\). Die \(\hat{x}^n\)-Terme in \(H\) spielen dagegen im Kommutator \( [ \hat{x}, H ] \) keine Rolle, da sie mit \( \hat{x} \) vertauschen. Also haben wir \[ \frac{i}{\hbar} \, [H, \hat{x}] = -\frac{i}{\hbar} \, [\hat{x}, H] = \frac{d}{d\hat{p}} H \] Für den Erwartungswert gilt also: \[ \frac{d}{dt} \langle \psi | \, \hat{x} \, \psi \rangle = \] \[ = \frac{i}{\hbar} \, \langle \psi (t) | \, [H, \hat{x}] \, \psi (t) \rangle = \] \[ = \langle \psi (t) | \, \frac{d}{d\hat{p}} H \, \psi (t) \rangle \] Diese Gleichung geht im klassischen Grenzfall in die klassische Hamiltonsche Bewegungsgleichung \[ \frac{d}{dt} x(t) = \frac{dH}{dp} \] über, denn aus den Mittelwerten der Messung werden bei verschwindender Streuung die klassischen Bewegungsgrößen. Analog kann man auch die zweite Hamiltonsche Bewegungsgleichung herleiten. Wir sehen also: Der klassische Grenzfall funktioniert mit unserem Quantisierungs-Kochrezept von oben tatsächlich!
Wir wissen also nun, wie die Kommutatoren unserer Operatoren aussehen sollen. Mehr braucht man streng genommen gar nicht zu wissen (so lässt sich beispielsweise die Quantenmechanik des eindimensionalen harmonischen Oszillators mit \( V(x) = a x^2 \) alleine mit Hilfe der Kommutatoren berechnen). Dies war der Weg, den Werner Heisenberg bei der Formulierung der Quantenmechanik beschritten hatte, wobei er durch das Einfügen von Basisvektoren die Operatorschreibweise noch in eine formale Schreibweise mit unendlichdimensionalen Matrizen umgeformt hatte (genau genommen startete er direkt mit solchen Matrizen).
Für unsere Anschauung und auch für Berechnungen ist es jedoch oft nützlich, einen konkreten Hilbertraum und eine dazugehörende Darstellungen der Operatoren auf diesem Hilbertraum zu finden, so dass die Kommutatoren gleichsam nebenbei korrekt herauskommen.
Eine Möglichkeit, dies für die nichtrelativistische Quantenmechanik zu erreichen, ist die Folgende:
Wähle als Hilbertraum den Raum der quadratintegrierbaren glatten
komplexwertigen Funktionen im dreidimensionalen reellen Raum,
d.h. der Funktionswert \( \psi(\boldsymbol{x}) \) ist eine komplexe Zahl und
das Argument \(\boldsymbol{x}\) der Funktion ist
ein dreidimensionaler reeller Vektor, der mit seinen drei Komponenten einen Ort im Raum charakterisiert.
Das Skalarprodukt ist in diesem Orts-Raum gegeben durch das Raumintegral
\[
\langle \phi | \psi \rangle =
\int \phi^*(\boldsymbol{x}) \, \psi(\boldsymbol{x}) \, d^3x
\]
wobei der Stern die komplexe Konjugation bezeichnet
(sodass \( (a + i b)^* = a - i b \) ist).
Wir definieren nun
die Operatoren \(\boldsymbol{\hat{x}}\) und \(\boldsymbol{\hat{p}}\) durch
\begin{align}
[\boldsymbol{\hat{x}} \psi](\boldsymbol{x}) &:= \boldsymbol{x} \cdot \psi(\boldsymbol{x}) \\
& \\
[\boldsymbol{\hat{p}} \psi](\boldsymbol{x}) &:= \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \psi(\boldsymbol{x})
\end{align}
Man kann nun leicht nachweisen, dass diese Operatoren bezüglich dem oben definierten
Skalarprodukt hermitesch sind und dass die gewünschten Kommutator-Beziehungen erfüllt sind.
Diese sogenannte Ortsdarstellung wählte Erwin Schrödinger und schuf damit etwa zeitgleich
zu Heisenberg einen anderen Zugang zur Quantenmechanik. Beide Zugänge sind äquivalent, wie
wir ja nun bereits wissen.

Credit: Nobel foundation,
Quelle:
Wikimedia Commons File:Erwin Schrödinger (1933).jpg, Public Domain
Im Prinzip könnten wir nun versuchen, uns an die Quantisierung anderer Theorien zu machen, beispielsweise der Elektrodynamik (das ist die relativistische Theorie der elektrischen und magnetischen Felder). Es zeigt sich jedoch, dass ein zweiter Zugang zur Quantentheorie häufig sehr nützlich ist, da er viele Zusammenhänge sehr viel deutlicher sichtbar macht, als es die kanonische Quantisierung von oben vermag. Insbesondere erhält man einen intuitiven Zugang zur Quantentheorie über ein einfaches Prinzip, und es wird sehr viel klarer, was der klassische Grenzfall genau bedeutet – in der mehr formalen kanonischen Quantisierung mutet der Übergang von Poissonklammern zu Kommutatoren ja manchmal etwas wie Zauberei an, und der klassische Grenzfall erfordert eine gewisse Mühe.
Der alternative Zugang geht im Wesentlichen auf den Physiker und Nobelpreisträger Richard Feynman aus dem Jahre 1942 zurück. Feynman versuchte (aufbauend auf Vorarbeiten von Paul Dirac), den etwas künstlichen Umweg über den Hamilton-Formalismus zu vermeiden und direkt von der Lagrange-Funktion auszugehen. So wie man die klassische Mechanik im Lagrangeformalismus oder alternativ nach einer Legendre-Transformation im Hamiltonformalismus formulieren kann, so sollte es auch möglich sein, die Quantentheorie wahlweise in einem Lagrange-Formalismus oder in dem oben gezeigten Hamilton-Formalismus darzustellen.
Ausgangspunkt der Formulierung Feynmans ist die Wahrscheinlichkeitsamplitude dafür, dass ein Teilchen, welches zur Zeit \(t'\) am Ort \(\boldsymbol{x}'\) startet, zur späteren Zeit \(t\) am Ort \(\boldsymbol{x}\) ankommt. Diese Amplitude bezeichnet man auch als Propagator. Wir wollen sie symbolisch durch das Skalarprodukt \[ \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \] abkürzen. Kennt man diesen Propagator, so lassen sich daraus alle anderen quantenmechanischen Größen berechnen.
Feynmans zentrale Idee bestand nun darin, die Interferenzregel aus dem letzten Kapitel als zentrale Forderung zu verwenden, um mit ihrer Hilfe den Propagator zu berechnen. Erinnern wir uns:
Die verschiedenen ununterscheidbaren Möglichkeiten sind hier die verschiedenen Wege, die das Teilchen nehmen kann, um in der Zeit von \(t'\) bis \(t\) vom Ort \(\boldsymbol{x}'\) zum Ort \(\boldsymbol{x}\) zu gelangen. Diese Möglichkeiten sind tatsächlich ununterscheidbar, wenn wir nur am Ort \(\boldsymbol{x}\) nach dem Teilchen suchen. Versuchen wir dagegen, zu messen, welchen Weg das Teilchen tatsächlich genommen hat, so haben wir es mit einem anderen Ereignis zu tun, zu dem auch eine andere Amplitude gehört. Dies wird am Doppelspaltexperiment sehr deutlich (wir wollen hier nicht näher darauf eingehen).
Jeder Weg, der innerhalb des Zeitintervalls von \(t'\) bis \(t\) vom Ort \(\boldsymbol{x}'\) zum Ort \(\boldsymbol{x}\) führt, steuert nach der Interferenzregel eine Amplitude (also eine komplexe Zahl, d.h. einen zweidimensionalen Pfeil) zum Propagator bei. Man muss nun alle diese Amplituden für alle diese Wege bzw. Pfade aufsummieren (oder genauer: integrieren), um den Propagator auszurechnen. Daher bezeichnet man den den entsprechenden mathematischen Ausdruck als Pfadintegral.
Gehen wir wieder von der klassischen Mechanik aus, deren Lagrangefunktion uns ja bekannt ist. Um mit Hilfe der Pfadintegralmethode eine dazu passende Quantentheorie zu konstruieren, müssen wir nun einen konkreten Pfadintegral-Ausdruck für den Propagator gleichsam erraten, und zwar wieder so, dass im klassischen Grenzfall die klassische Mechanik entsteht.
Wir wollen hier jedoch etwas anders vorgehen, da wir ja bereits die Methode der kanonischen Quantisierung kennen: wir versuchen, aufgrund der kanonischen Quantisierung der klassischen Mechanik einen Ausdruck für das Pfadintegral herzuleiten. Damit wäre dann garantiert, dass dieses Pfadintegral dieselbe Quantentheorie ergibt wie die kanonische Quantisierung, wenn man es als Ausgangspunkt für die Quantisierung der klassischen Mechanik verwendet.
Machen wir uns zunächst mit dem Propagator vertraut. Um die Diskussion zu vereinfachen, wollen wir ganz konkret die Darstellung des Zustandsvektors durch eine komplexwertige Funktion \(\psi(t,\boldsymbol{x})\) verwenden (diesmal allerdings mit nur einer Raumdimension).
Die folgende Gleichung definiert den Propagator \(\langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle\) als Integralkern: \[ \psi(t,\boldsymbol{x}) = \int d^3x' \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \; \psi(t',\boldsymbol{x}') \] wobei wir \(t > t'\) verlangen, denn wir wollen ja sehen, wie sich die Funktion bei wachsender Zeit entwickelt. Man spricht daher auch vom kausalen Propagator.
Die Idee hinter dieser Gleichung ist analog zum Huygensschen Prinzip der Optik: Zur Zeit \(t'\) geht von jedem Punkt \(\boldsymbol{x}'\) eine Elementarwelle aus, deren Anfangswert proportional zu \(\psi(t',\boldsymbol{x}')\) ist. Zur Zeit \(t\) hat diese Elementarwelle am Zielort \(\boldsymbol{x}\) dann die Stärke \[ \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \; \psi(t',\boldsymbol{x}') \] Nun muss man alle Elementarwellen der verschiedenen Startpunkte \(\boldsymbol{x}'\) aufsummieren (aufintegrieren), um die Gesamtwelle \(\psi(t,\boldsymbol{x})\) zur späteren Zeit \(t\) am Ort \(\boldsymbol{x}\) zu erhalten. Die Wellen interferieren also miteinander.
In der Quantentheorie entsprechen den Wellen die Wahrscheinlichkeitsamplituden, und es wird über die verschiedenen ununterscheidbaren Möglichkeiten integriert. Der Propagator entspricht der Wahrscheinlichkeitsamplitude dafür, dass das Teilchen zur Zeit \(t'\) am Ort \(\boldsymbol{x}'\) startet und zur späteren Zeit \(t\) am Ort \(\boldsymbol{x}\) ankommt. Weiter ist \(\psi(t',\boldsymbol{x}')\) die Amplitude dafür, dass sich das Teilchen zur Zeit \(t'\) am Startort \(\boldsymbol{x}'\) befindet, und analog ist \(\psi(t,\boldsymbol{x})\) die Amplitude dafür, dass das Teilchen schließlich zur Zeit \(t\) am Zielort \(\boldsymbol{x}\) gemessen wird. Die obige Integralformel spiegelt also lediglich die Interferenzregel der Quantentheorie wieder.
Der Propagator ist streng genommen mathematisch keine Funktion, sondern eine sogenannte Distribution. Er macht nur im Zusammenhang mit Integralen wie oben Sinn. Das sieht man beispielsweise, wenn man den Spezialfall \( t = t' \) betrachtet (genauer betrachtet man den Grenzwert, bei dem \(t\) von oben gegen \(t'\) geht). Dann muss \[ \psi(t',\boldsymbol{x}) = \int d^3x' \; \langle t', \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \; \psi(t',\boldsymbol{x}') \] gelten, d.h. \[ \langle t', \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle = \delta(\boldsymbol{x} - \boldsymbol{x}') \] Dabei ist \( \delta(\boldsymbol{x} - \boldsymbol{x}') \) die bekannte Delta-Distribution, die über die Eigenschaft \[ \int d^3x \; \delta(\boldsymbol{a} - \boldsymbol{x}) \; f(\boldsymbol{x}) = f(\boldsymbol{a}) \] definiert ist. Man kann sich \( \delta(\boldsymbol{a} - \boldsymbol{x}) \) als Gaußsche Glockenkurve in der Variable \(\boldsymbol{x}\) mit Maximum bei \(\boldsymbol{a}\) vorstellen, die unendlich schmal und hoch geworden ist (wobei der Grenzwert genau genommen nur für Integrale mit dieser Glockenkurve definiert ist und nicht für die Glockenkurve selbst). Sie entspricht also einem unendlich hohen und unendlich schmalen Peak beim Wert \(\boldsymbol{a}\). Insbesonderen ist \( \delta(\boldsymbol{a} - \boldsymbol{x}) = 0 \) für \(\boldsymbol{x} \ne \boldsymbol{a}\).
Was können wir nun über den Propagator herausfinden? Man kann z.B. zeigen, dass der Propagator die sogenannte Greensche Funktion des Operators \( i \hbar \frac{d}{dt} - H \) bildet, also in gewissem Sinne sein Inverses ist, denn es gilt \[ ( i \hbar \frac{d}{dt} - H ) \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle = \] \[ = i \hbar \, \delta(t-t') \, \delta(\boldsymbol{x}-\boldsymbol{x}') \] Diese Gleichung ist im Distributionensinn zu verstehen und benötigt zusätzliche Randbedingungen, die wir hier nicht im Detail aufführen wollen – diese Randbedingungen werden benötigt, um die obige Integralgleichung zu reproduzieren, die ja nur für \(t > t'\) gelten soll. Für \(t > t'\) folgt \[ ( i \hbar \frac{d}{dt} - H ) \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle = 0 \] Diese wichtige Gleichung für den Propagator können wir auch direkt aus der Schrödingergleichung \( 0 = (i \hbar \frac{d}{dt} - H) \; \psi(t,\boldsymbol{x}) \) ableiten, indem wir darin die obige Integraldarstellung der Wellenfunktion einsetzen. Die Rechnung geht so (wobei wir \(t > t'\) voraussetzen): \begin{align} 0 &= (i \hbar \frac{d}{dt} - H) \, \psi(t,\boldsymbol{x}) = \\ & \\ &= (i \hbar \frac{d}{dt} - H) \, \int d^3x' \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \; \psi(t',\boldsymbol{x}') = \\ & \\ &= \int d^3x' \; \left( (i \hbar \frac{d}{dt} - H) \, \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \right) \; \psi(t',\boldsymbol{x}') \end{align} denn \( (i \hbar \frac{d}{dt} - H) \) wirkt ja nur auf die ungestrichenen Variablen \(t\) und \(\boldsymbol{x}\). Also muss die große Klammer im Integral für \(t > t'\) gleich Null sein, damit auch das gesamte Integral für beliebige Funktionen \(\psi(t',\boldsymbol{x}')\) Null wird. Das ergibt dann unsere obige Gleichung.
Wenn man den Propagator kennt, so hat man die Schrödingergleichung gelöst, denn man kann \(\psi(t,\boldsymbol{x})\) (zumindest im Prinzip) berechnen. Anstatt die Schrödingergleichung zu lösen, kann man also auch versuchen, den Propagator und mit seiner Hilfe dann \(\psi(t,\boldsymbol{x})\) zu berechnen. Ja man kann sogar sagen: Hat man eine Formel für den Propagator, so braucht man die Schrödingergleichung nicht mehr. Genau dies hat Richard Feynman getan. Schauen wir uns dazu nun die Details an!
In der Integralgleichung \[ \psi(t,\boldsymbol{x}) = \int d^3x' \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \; \psi(t',\boldsymbol{x}') \] können wir die Wellenfunktion \(\psi(t',\boldsymbol{x}')\) rechts im Integral natürlich ihrerseits durch ein entsprechendes Integral mit einem noch früheren Zeitpunkt \(t''\) ausdrücken, so dass aus der obigen Formel die Doppel-Integral-Gleichung \[ \psi(t,\boldsymbol{x}) = \int d^3x' \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \] \[ \int d^3x'' \; \langle t', \boldsymbol{x}' \, | \, t'', \boldsymbol{x}'' \rangle \; \psi(t'',\boldsymbol{x}'') \] wird. Dieses Spiel können wir beliebig oft wiederholen.
Wir können dies nun verwenden, um das Zeitintervall von \(t'\) bis \(t\) in \(n\) gleich große Teilintervalle \( \Delta t = (t - t')/n \) zu zerlegen. Später werden wir dann den Grenzfall \(n\) gegen Unendlich untersuchen, bei dem die Teilintervalle \( \Delta t \) beliebig klein werden. Die entsprechende Formel lautet dann \[ \psi(t,\boldsymbol{x}) = \int d^3x_0 \, d^3x_1 \, ... \, d^3x_{n-1} \] \[ \langle t, \boldsymbol{x} \, | \, t_{n-1}, \boldsymbol{x}_{n-1} \rangle \] \[ \langle t_{n-1}, \boldsymbol{x}_{n-1} \, | \, t_{n-2}, \boldsymbol{x}_{n-2} \rangle \] \[ ... \] \[ \langle t_1, \boldsymbol{x}_1 \, | \, t_0, \boldsymbol{x}_0 \rangle \; \psi(t_0,\boldsymbol{x}_0) \] Der Index dient dazu, die verschiedenen Integrationsvariablen zu unterscheiden, ist also nicht mit einem Index für eine Raumachse zu verwechseln.
Picken wir uns ein Zeitintervall von \(t_{i-1}\) bis \(t_i\) heraus, wobei \(i\) irgendein Index zwischen \(1\) und \(n\) ist. Wir haben oben gesehen, dass wegen \( t_i > t_{i-1} \) der Propagator die Schrödingergleichung erfüllt: \[ ( i \hbar \frac{d}{dt_i} - H ) \; \langle t_i, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = 0 \] wobei die zeitliche Ableitung auf die spätere Zeit \(t_i\) links und der Hamiltonoperator auf die linke Ortsvariable \(\boldsymbol{x}_i\) wirkt. Die formale Lösung dieser Gleichung lautet \[ \langle t_i, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = e^{-i H \Delta t / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle \] mit \( \Delta t = t_i - t_{i-1} \), wobei die Exponentialfunktion mit dem Hamiltonoperator \(H\) im Exponenten als Potenzreihe \(e^x = 1 + x + x^2/2 + \, ... \, \) definiert ist. Dabei steht hinter der Exponentialfunktion der Propagator mit zwei gleichen Zeitkoodinaten \(t_{i-1}\), der durch die Delta-Funktion (genauer: Distribution) gegeben ist, wie wir von oben wissen: \[ \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \delta(\boldsymbol{x}_i - \boldsymbol{x}_{i-1}) \] Die Gleichung ist also wieder im Distributionensinn zu verstehen: Man stelle sich statt der Delta-Funktion eine Glockenkurve vor, bilde Integrale über das Ganze (der Propagator ist ja als Integralkern definiert) und betrachte den Grenzfall, bei dem die Glockenkurve unendlich schmal und hoch wird.
Dass die obige Formel tatsächlich eine Lösung der Schrödingergleichung darstellt, sieht man leicht so: \[ ( i \hbar \frac{d}{dt_i} - H ) \; \langle t_i, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = ( i \hbar \frac{d}{dt_i} - H ) \; e^{-i H (t_i - t_{i-1}) / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = (H - H ) \; e^{-i H (t_i - t_{i-1}) / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = 0 \] Nun ist in der nichtrelativistischen Quantenmechanik der Hamiltonoperator \(H\), der auf die Ortsvariable \(\boldsymbol{x}_i\) wirkt, gegeben durch \[ H = \frac{\boldsymbol{\hat{p}}_i^2}{2m} + V(\boldsymbol{x}_i) \] mit dem Potential \(V(\boldsymbol{x}_i)\), der Masse \(m\) und dem Impulsoperator \[ \boldsymbol{\hat{p}}_i = \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}_i} \] Im Potential haben wir dabei den Ortsoperator \(\boldsymbol{\hat{x}}_i\) direkt durch die Ortsvariable \(\boldsymbol{x}_i\) ersetzt, da in der hier verwendeten Ortsdarstellung beides identisch ist.
Für sehr kleine Zeitintervalle \( \Delta t = t_i - t_{i-1} \) ist dann \[ \langle t_i, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = e^{-i H \Delta t / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle \] \[ = e^{-i \, \left( \frac{\boldsymbol{\hat{p}}_i^2}{2m} + V(\boldsymbol{x}_i) \right) \, \Delta t / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle \approx \] \[ \approx e^{-i \, V(\boldsymbol{x}_i) \, \Delta t / \hbar} \cdot e^{-i \, \frac{\boldsymbol{\hat{p}}_i^2}{2m} \, \Delta t / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle \] wie man mit Hilfe der sogenannten Baker-Campbell-Hausdorff-Formel nachweisen kann. Wenn man diese Baker-Campbell-Hausdorff-Formel anwendet und dabei höhere Potenzen von \(\Delta t\) im Grenzfall sehr kleiner \(\Delta t\)-Werte vernachlässigt, ergibt sich das obige Ergebnis. Physikalisch bedeutet das, dass wir den Transfer zwischen kinetischer und potentieller Energie im winzigen Zeitintervall \(\Delta t\) vernachlässigen, weil wir davon ausgehen, dass das Potential \(V(\boldsymbol{x}_i)\) hinreichend gutartig (also glatt) ist.
Nun kommen einige heuristische Argumente, die streng genommen einer genauen mathematischen Untersuchung bedürfen. Wir wollen uns hier nicht in die mathematischen Details stürzen, sondern eher anschaulich argumentieren.
Zunächst einmal wollen wir annehmen, dass bei kleinen Zeitintervallen nur diejenigen Propagatoren \( \langle t_i, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle \) nennenswert zum Gesamtintegral beitragen, bei denen auch die Orte \(\boldsymbol{x}_i\) und \(\boldsymbol{x}_{i-1}\) nahe beieinander liegen (dazu kann entweder der Propagator bei größeren räumlichen Abständen selbst klein sein, oder aber er oszilliert so schnell, dass sich die verschiedenen Propagatorbeiträge im Integral wegheben (destruktive Interferenz) ). Es soll also relativ unwahrscheinlich sein, dass das Teilchen in sehr kurzer Zeit mehr als nur ein kleines Stück Weg zurücklegt. Daher wollen wir das Potential am Zielort \(V(\boldsymbol{x}_i)\) durch den klassischen Potentialwert in der Ortsmitte zwischen Start- und Zielort \( V(\frac{1}{2}(\boldsymbol{x}_i + \boldsymbol{x}_{i-1}))\) ersetzen.
Bleibt noch der Term \[ e^{-i \, \frac{\boldsymbol{\hat{p}}_i^2}{2m} \, \Delta t / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle \] mit dem Impulsoperator \(\boldsymbol{\hat{p}}\) zu betrachten. Dies ist gerade der Propagator für ein freies Teilchen, den man explizit berechnen kann. Dazu drückt man den Propagator durch ein Fourierintegral aus, so dass der Impulsoperator darin zu einer reellen Zahl wird, und berechnet das Fourierintegral durch analytische Fortsetzung mit Hilfe des Residuensatzes, wobei man die Randbedingung zu berücksichtigen hat, dass wir einen kausalen Propagator betrachten, der nur für \(t_i > t_{i-1}\) definiert ist (dies führt zu einer entsprechenden infinitesimalen Verschiebung der Pole im Fourierintegral). Siehe auch Wikipedia: Propagator (propagator of a one-dimensional free particle). Hier ist das Ergebnis für den freien kausalen Propagator: \[ e^{-i \, \frac{\boldsymbol{\hat{p}}_i^2}{2m} \, \Delta t / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = \left( \frac{m}{i h \Delta t} \right)^\frac{3}{2} \, e^{i \, \frac{m \, (\boldsymbol{x}_i - \boldsymbol{x}_{i-1})^2}{2 \, \hbar \, \Delta t} } \] Insgesamt ist also unser Propagator für sehr kleine \(\Delta t\) (sodass wir \( \approx \) durch \( = \) ersetzen können) dann gleich \[ \langle t_i, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = e^{-i \, V(\boldsymbol{x}_i) \, \Delta t / \hbar} \cdot e^{-i \, \frac{\boldsymbol{\hat{p}}_i^2}{2m} \, \Delta t / \hbar} \, \langle t_{i-1}, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = e^{-i \, V(\frac{1}{2}(\boldsymbol{x}_i + \boldsymbol{x}_{i-1})) \, \Delta t / \hbar} \cdot \left( \frac{m}{i h \Delta t} \right)^\frac{3}{2} \, e^{i \, \frac{m \, (\boldsymbol{x}_i - \boldsymbol{x}_{i-1})^2}{2 \, \hbar \, \Delta t} } = \] \[ = \left( \frac{m}{i h \Delta t} \right)^\frac{3}{2} \, e^{i \, \frac{\Delta t}{\hbar} \, \left( \frac{m \, (\boldsymbol{x}_i - \boldsymbol{x}_{i-1})^2}{2 \, (\Delta t)^2} - V(\frac{1}{2}(\boldsymbol{x}_i + \boldsymbol{x}_{i-1})) \right) } \] \[ =: \left( \frac{m}{i h \Delta t} \right)^\frac{3}{2} \, e^{i \, \frac{\Delta t}{\hbar} \, \left( \frac{m}{2} \boldsymbol{v}_i^2 - V(\boldsymbol{\bar{x}}_i) \right) } \] mit der Geschwindigkeit \( \boldsymbol{v}_i = \frac{\boldsymbol{x}_i - \boldsymbol{x}_{i-1}}{\Delta t} \) und dem Mittelwerts-Ort \( \boldsymbol{\bar{x}}_i = \frac{1}{2}(\boldsymbol{x}_i + \boldsymbol{x}_{i-1}) \). Im Exponenten steht also die klassische Lagrangefunktion eines Teilchens in einem Potential, d.h. wir haben für sehr kleine Zeitintervalle \(\Delta t\) für den Propagator die Beziehung \[ \langle t_i, \boldsymbol{x}_i \, | \, t_{i-1}, \boldsymbol{x}_{i-1} \rangle = \] \[ = \left( \frac{m}{i h \Delta t} \right)^\frac{3}{2} \, e^{i \, \frac{\Delta t}{\hbar} \, L(\boldsymbol{\bar{x}}_i, \boldsymbol{v}_i)} \] Nun sind wir gerüstet, um uns auch größere Zeitintervalle anzusehen. Dabei führen wir den Grenzwert für unendlich viele Zeitintervalle durch und erhalten: \[ \psi(t,\boldsymbol{x}) = \] \[ = \lim_{n \rightarrow \infty} \, \int d^3x_0 \, d^3x_1 \, ... \, d^3x_{n-1} \] \[ \langle t, \boldsymbol{x} \, | \, t_{n-1}, \boldsymbol{x}_{n-1} \rangle \] \[ \langle t_{n-1}, \boldsymbol{x}_{n-1} \, | \, t_{n-2}, \boldsymbol{x}_{n-2} \rangle \] \[ ... \] \[ \langle t_1, \boldsymbol{x}_1 \, | \, t_0, \boldsymbol{x}_0 \rangle \cdot \] \[ \cdot \psi(t_0,\boldsymbol{x}_0) = \] \[ = \lim_{n \rightarrow \infty} \, \int d^3x_0 \, d^3x_1 \, ... \, d^3x_{n-1} \, \left(\frac{m}{i h \Delta t}\right)^{\frac{3n}{2}} \] \[ e^{i \, \frac{\Delta t}{\hbar} \, L(\boldsymbol{\bar{x}}_n, \boldsymbol{v}_n)} e^{i \, \frac{\Delta t}{\hbar} \, L(\boldsymbol{\bar{x}}_{n-1}, \boldsymbol{v}_{n-1})} \, ... \, e^{i \, \frac{\Delta t}{\hbar} \, L(\boldsymbol{\bar{x}}_1, \boldsymbol{v}_1)} \] \[ \cdot \psi(t_0,\boldsymbol{x}_0) = \] Das Produkt der e-Funktionen können wir noch zu einer einzigen e-Funktion zusammenfassen. Außerdem können wir mit die Definition des Propagators verwenden: \[ \psi(t,\boldsymbol{x}) = \int d^3x' \; \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle \; \psi(t',\boldsymbol{x}') \] für den Propagator verwenden und so den Propagator für größere Zeitintervalle aus der obigen Formel ablesen (dabei setzen wir \(t' = t_0\) und \(\boldsymbol{x}' = \boldsymbol{x}_0 \) sowie \(t = t_n\) und \(\boldsymbol{x} = \boldsymbol{x}_n \) ): \[ \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle = \] \[ = \lim_{n \rightarrow \infty} \, \int d^3x_1 \, ... \, d^3x_{n-1} \, \left(\frac{m}{i h \Delta t}\right)^{\frac{3n}{2}} \] \[ e^{ i \, \frac{\Delta t}{\hbar} \, \left( L(\boldsymbol{\bar{x}}, \boldsymbol{v}) + L(\boldsymbol{\bar{x}}_{n-1}, \boldsymbol{v}_{n-1}) + \, ... \, + L(\boldsymbol{\bar{x}}_1, \boldsymbol{v}_1) \right) } \] Es werden also zwischen den Punkten \(\boldsymbol{x}'\) und \(\boldsymbol{x}\) unendlich viele Zwischenebenen eingefügt (genau genommen \(n-1\) Zwischenebenen, woraus dann im Grenzfall unendlich viele werden) und es werden alle Propagationen von \(\boldsymbol{x}'\) zur ersten Zwischenebene, von dort zur zweiten Zwischenebene usw. aufsummiert, bis schließlich die Propagation der letzten Zwischenebene zum Punkt \(\boldsymbol{x}\) betrachtet wird. Jede Zwischenebene entspricht einer Integration \( \int d^3x_i \) mit \(i\) von \(1\) bis \(n-1\). Die Propagation von einer Zwischenebene zur nächsten dauert dabei die Zeit \( \Delta t = (t - t')/n \), was im Grenzfall beliebig klein wird. Der Faktor \( \left(\frac{m}{i h \Delta t}\right)^{\frac{3n}{2}} \) sorgt für die richtige Normierung.
Ob sich der Grenzwert für \(n\) gegen Unendlich mathematisch sauber durchführen lässt, ist eine schwierige Frage, die weit über den Rahmen dieses Kapitels hinausführt. Immerhin hat man es mit unendlich vielen Integrationen über oszillierende komplexwertige Integranden zu tun. Für die Praxis kann man aber immer auf die obige Darstellung zurückgehen, um beispielsweise numerische Berechnungen mit größeren (aber endlichen) Werten für \(n\) durchzuführen.
Man kann sich den obigen Ausdruck noch etwas anders veranschaulichen. Dazu nehmen wir vereinfacht an, dass der Ort nur diskrete Werte annehmen kann, so dass aus den Integralen Summen werden. Wie wir sehen, wird dann im obigen Ausdruck über alle Ortskombinationen summiert, die sich aus den Orten der ersten, zweiten usw. bis zur \(n-1\) -ten Zwischenebene bilden lassen. Jede dieser Ortskombinationen können wir als Vekor \( (\boldsymbol{x}', \boldsymbol{x}_1, \boldsymbol{x}_2, \, ... \, , \boldsymbol{x}_{n-1}, \boldsymbol{x}) \) schreiben, wobei der Anfangspunkt \(\boldsymbol{x}'\) und der Endpunkt \(\boldsymbol{x}\) fest vorgegeben sind, und die Orte der Zwischenebenen alle Werte annehmen können. Über alle diese Vektoren wird summiert.
Nun kann man den Vektor
\( (\boldsymbol{x}', \boldsymbol{x}_1, \boldsymbol{x}_2, \, ... \, , \boldsymbol{x}_{n-1}, \boldsymbol{x}) \)
auch als Polygonzug (gezackten Weg) zwischen den Punkten \(\boldsymbol{x}'\) und \(\boldsymbol{x}\)
über die Zwischenpunkte \( \boldsymbol{x}_i \) interpretieren und sagen,
dass über all diese Polygonzüge summiert wird. Im Grenzfall
unendlich großer \(n\) wird aus der Summe über alle Polygonzüge die
Summe über alle stetigen Wege zwischen \(\boldsymbol{x}'\) und \(\boldsymbol{x}\)
(an dieser Stelle muss man streng genommen vorsichtig sein, welche Wege genau
zugelassen sind – man denke an fraktale Kurven und ähnliche mathematische
Monster; es zeigt sich, dass
beim Grenzübergang unendlich kleiner \(\Delta t\) der Betrag
\( |\boldsymbol{x}_i - \boldsymbol{x}_{i-1}| \)
mindestes so schnell schrumpfen muss wie \( \sqrt{\Delta t} \) ).
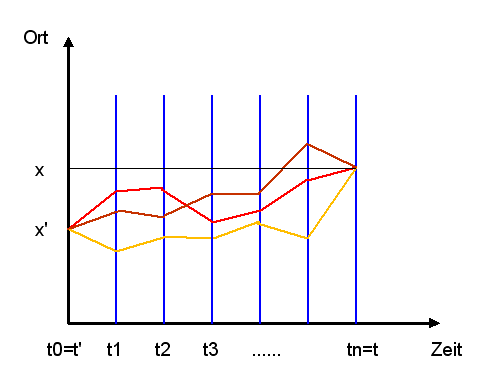
Schauen wir uns nun den Exponenten der e-Funktion an. Er lautet: \[ i \, \frac{\Delta t}{\hbar} \, ( L(\boldsymbol{\bar{x}}, \boldsymbol{v}) + L(\boldsymbol{\bar{x}}_{n-1}, \boldsymbol{v}_{n-1}) + \] \[ + \, ... \, + L(\boldsymbol{\bar{x}}_1, \boldsymbol{v}_1) ) \] d.h. für jeden Polygonzug werden die Werte der Lagrangefunktion für jeden Übergang von einer Zwischenebene zur nächsten ausgewertet und mit \(\Delta t\) gewichtet aufsummiert. Im Grenzfall \(n \rightarrow \infty\) wird daraus das Integral über \(dt'' = \Delta t\) entlang des Weges \(\boldsymbol{x}(t'')\), der durch den Polygonzug approximiert wird, also (bis auf den Vorfaktor) das Wirkungsfunktional \(S[x]\) für den Polygonzug-Weg \(\boldsymbol{x}(t'')\): \[ \frac{i}{\hbar} \, \int_{t'}^t dt'' \, L(\boldsymbol{\boldsymbol{x}(t'')}, \boldsymbol{v}(t'')) = \frac{i}{\hbar} \, S[\boldsymbol{x}] \] Wir wollen das Integral über alle Orte der unendlich vielen Zwischenebenen nun formal in ein Integral über alle Wege \(\boldsymbol{x}(t'')\) umschreiben, die vom Ort \(\boldsymbol{x}'\) zur Zeit \(t'\) zum Ort \(\boldsymbol{x}\) zur Zeit \(t\) führen. Dieses Integral verstehen wir als Grenzwert der Summe über alle Polygonzüge mit \(n-1\) Zwischenebenen, wobei wir einerseits \(n\) gegen unendlich gehen lassen und andererseits wieder kontinuierlich viele \(\boldsymbol{x}_i\)-Werte in den Zwischenebenen zulassen. Man bezeichnet dieses Integral auch als Pfadintegral: \[ \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle = \] \[ = \lim_{n \rightarrow \infty} \, \int d^3x_1 \, ... \, d^3x_{n-1} \, \left(\frac{m}{i h \Delta t}\right)^{\frac{3n}{2}} \] \[ e^{ i \, \frac{\Delta t}{\hbar} \, \left( L(\boldsymbol{\bar{x}}, \boldsymbol{v}) + L(\boldsymbol{\bar{x}}_{n-1}, \boldsymbol{v}_{n-1}) + \, ... \, + L(\boldsymbol{\bar{x}}_1, \boldsymbol{v}_1) \right) } = \] \[ =: \int_{\mathrm{Wege} \; \boldsymbol{x}} \, \mathcal{D}\boldsymbol{x} \; e^{ \frac{i}{\hbar} \, S[\boldsymbol{x}] } \] Dabei soll \( \mathcal{D}\boldsymbol{x} \) im Funktionenraum der Wege \(\boldsymbol{x}(t'')\) ein geeignetes Maß sein, wie es sich durch die Grenzwertbildung oben ergibt. Irgendwie muss also das Produkt der unendlich vielen Maße \( d^3x_1 \, ... \, d^3x_{n-1} \) multipliziert mit dem Normierungsfaktor \( \left(\frac{m}{i h \Delta t}\right)^{\frac{3n}{2}} \) im Grenzfall unendlich großer \(n\) das Maß \( \mathcal{D}\boldsymbol{x} \) im Raum der Wege ergeben.
Mathematisch ist dieser Übergang zum Maß \( \mathcal{D}\boldsymbol{x} \) ziemlich komplex und voller Fallen – so sagt ein Satz von A. Weil, dass es im obigen naiven Sinn ein solches Maß nicht gibt (siehe z.B. Markus J. Pflaum: Gibt es in der Mathematik ein Pfadintegral?, Habilitationsvortrag vom 10. Januar 2001 (ps-File)). Man kann versuchen, das Vorgehen zu präzisieren und z.B. das sogenannte Wiener-Maß verwenden. Letztlich läuft es darauf hinaus, dass man nur hinreichend gutartige Pfade (Wege) zulässt. Genau diese Annahme haben wir sowieso an mehreren Stellen in unserer obigen Argumentation bereits verwendet.
Das Feynmansche Pfadintegral \[ \langle t, \boldsymbol{x} \, | \, t', \boldsymbol{x}' \rangle = \int_{\mathrm{Wege} \; \boldsymbol{x}} \, \mathcal{D}\boldsymbol{x} \; e^{ \frac{i}{\hbar} \, S[\boldsymbol{x}] } \] hat eine recht anschauliche Interpretation: Ein Teilchen, das zur Zeit \(t'\) am Ort \(\boldsymbol{x}'\) startet und zur Zeit \(t\) am Ort \(\boldsymbol{x}\) ankommt, probiert alle (ununterscheidbaren) Möglichkeiten (also alle Wege) aus. Jeder dieser Wege trägt mit der Amplitude \( e^{ \frac{i}{\hbar} \, S[\boldsymbol{x}] } \) zur Gesamtamplitude bei, d.h. das Verhältnis Wirkungsfunktional des Weges zum Planckschen Wirkungsquantum \(\hbar\) bestimmt die Phase der Amplitude, die zu dem Weg gehört. Wenn Ihnen das merkwürdig vorkommt, dass ein Teilchen zugleich alle Wege ausprobiert: Genau genommen probiert seine Quantenwelle alle Wege aus, so wie es das Huygenssche Prinzip mithilfe von Elementarwellen veranschaulicht.
Nehmen wir nun an, dass wir relativ große (d.h. makroskopische) Orts- und Zeitabstände betrachten. Dann wird auch das Wirkungsfunktional für diese Wege zumeist sehr viel größer als das Plancksche Wirkungsquantum sein, denn es wird ja die Lagrangefunktion über entsprechend lange Wege aufintegriert. Auch eng benachbarte Wege werden daher meistens Wirkungen besitzen, die sich um deutlich mehr als das Plancksche Wirkungsquantum unterscheiden. Die Amplituden der meisten Wege werden also ganz unterschiedliche Phasen besitzen und sich im Wesentlichen gegenseitig auslöschen (destruktive Interferenz). Lediglich Wege, bei denen benachbarte Wege sich in ihrer Wirkung nur wenig unterscheiden, können sich konstruktiv aufsummieren und zum Gesamtergebnis nennenswert beitragen. Dies ist für Wege der Fall, in deren Nähe die Wirkung stationär wird, sich also bei kleiner Veränderung des Weges kaum ändert.
Solche Wege finden wir am Minimum des Wirkungsfunktionals. Der Weg mit minimaler Wirkung ist aber gerade eine Lösung des klassischen Variationsprinzips und damit eine Lösung der klassischen Euler-Lagrange-Gleichungen. Alle Wege in der unmittelbaren Nähe dieses klassischen Weges können konstruktiv miteinander interferieren, während die anderen Wege destruktiv interferieren und damit bedeutungslos werden. Man kann sagen, das Teilchen nimmt umso eher den klassischen Weg, je größer die Wirkung im Vergleich zum Planckschen Wirkungsquantum ist.
Den klassischen Grenzfall hatten wir weiter oben definiert durch den Grenzfall, dass das Plancksche Wirkungsquantum \(h\) gegen Null geht. Dies können wir nun präzisieren:
Damit haben wir eine ganz natürliche Begründung für das mysteriöse Prinzip der kleinsten Wirkung gefunden, mit dessen Hilfe wir oben die klassische Bewegungsgleichung formuliert haben. Und nun wissen wir auch, warum es nützlich war, die klassische Theorie mit Hilfe dieses Prinzips zu formulieren, um den Übergang zur entsprechenden Quantentheorie vorzubereiten.
Umgekehrt wird auch klarer, was es bedeutet, die Quantentheorie zu einer vorgegebenen klassischen Theorie zu konstruieren: Wir müssen alle Wertekombinationen berücksichtigen, die die dynamischen Variablen der Theorie annehmen können, zu jeder dieser Möglichkeiten das Wirkungsfunktional \(S\) berechnen (das kennen wir ja aufgrund der vorgegebenen klassischen Theorie) und die Möglichkeit mit der Amplitude \( e^{ \frac{i}{\hbar} S } \) zur Berechnung der Gesamtamplitude im Pfadintegral berücksichtigen. Je näher dabei die betrachteten Wirkungen in die Größenordnung des Planckschen Wirkungsquantums rücken, umso wichtiger werden auch die Möglichkeiten jenseits der klassischen Lösung. In diesem Sinn bedeutet Quantisierung das Berücksichtigen von Möglichkeiten (Fluktuationen) jenseits der klassischen Lösung.
Diese Methode funktioniert auch bei anderen Theorien als der klassischen Mechanik. Wir müssen uns nur über die dynamischen Variablen (Freiheitsgrade) der Theorie klar werden, ein passendes Wirkungsfunktional angeben und schon kann es losgehen. Dies wollen wir in den nächsten Kapiteln schrittweise versuchen, wobei wir sowohl die kanonische Quantisierung als auch Feynmans Pfadintegral-Quantisierung anwenden werden (es sollte ja in beiden Fällen die gleiche Quantentheorie herauskommen). Doch so einfach sich das Konzept anhört – der Teufel steckt wie so oft im Detail, und es ist gar nicht so einfach, unsere Quantisierungs-Kochrezepte konsistent umzusetzen. Wir sollten also noch auf einige Überaschungen gefasst sein.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 05 May 2023