
Werner Heisenberg (1901 - 1976),
Quelle: Wikimedia Commons File:Heisenberg 10.jpg, gemeinfrei.
Zusammenfassung des Buchkapitels:
Wie kann die Beschreibung eines Teilchens durch eine Welle in die Beschreibung durch eine Teilchenbahn übergehen? Wann reicht umgekehrt die Teilchenbahn nicht mehr aus, so dass man eine Wellenbeschreibung braucht? Die Antwort gibt u.a. Heisenbergs Unschärferelation.

Heisenbergs Unschärferelation sagt, dass bei einer Messung das Produkt aus
Ortsunsicherheit \( \Delta x \) und
Impulsunsicherheit \( \Delta p \) sich niemals unter einen bestimmten
Wert drücken lässt. Dieser Wert ist durch das Plancksche Wirkungsquantum
mal einem Zahlenfaktor gegeben:
\[
\Delta x \, \Delta p \ge \frac{\hbar}{2}
\]
Nichtrelativistisch ist \( p = m v \) mit der Teilchenmasse \(m\) und der
Teilchengeschwindigkeit \(v\) und es ergibt sich
\[
\Delta x \, m \, \Delta v \ge \frac{\hbar}{2}
\]
Die Heisenbergsche Unschärferelation ist eine unmittelbare Folge der
Überlagerungseigenschaften von Wellen und der Tatsache, dass sich
eine Wellenlänge in der Quantenmechanik in einen
Teilchenimpuls bzw. Teilchengeschwindigkeit
übersetzen lässt (man muss nämlich umso mehr ebene Wellen mit verschiedenen
Wellenlängen überlagern, je kleiner das Wellenpaket ist, das daraus entstehen soll).
Die Unschärferelation macht uns klar, warum wir niemals eine genaue Teilchenbahn angeben können. Dafür benötigen wir nämlich gleichzeitig den präzisen Ort und die genaue Geschwindigkeit des Teilchens. Beides ist jedoch nicht gleichzeitig mit beliebiger Genauigkeit bekannt, da es keine Wahrscheinlichkeitswelle gibt, die eine feste Wellenlänge besitzt und an einem einzigen Punkt startet. Ort und Impuls bzw. Teilchengeschwindigkeit sind komplementäre Messgrößen.
Da sich eine Frequenz in der Quantenmechanik in eine Teilchenenergie übersetzen lässt, folgt aus den Überlagerungseigenschaften von Wellen analog die Energie-Zeit-Unschärferelation (siehe auch Zusatzinfos unten) \[ \Delta E \, \Delta t \ge \frac{\hbar}{2} \]
In fact the smallest units of matter are not physical objects in the ordinary sense; they are forms, ideas which can be expressed unambiguously only in mathematical language.
(Werner Heisenberg zitiert in The New York Times Book Review (8 March 1992), siehe Wikiquote: Werner Heisenberg).
a) Orts-Impuls-Unschärfe und die Überlagerung von Wellen
b) Energie-Zeit-Unschärfe, Durchlaufzeit, Lebensdauer und Breit-Wigner-Resonanzkurve
Eine detaillierte (mathematische) Betrachtung der kanonischen Quantisierung der klassischen Mechanik inklusive Heisenbergscher Unschärferelation finden Sie in Quantenfeldtheorie und Eichfelder, Kapitel 3: Die Quantisierung der klassischen Mechanik (nur für Leser mit guten mathematischen und physikalischen Vorkenntnissen geeignet).
Warum muss man umso mehr ebene Wellen mit verschiedenen Wellenlängen überlagern, je kleiner das daraus entstehende Wellenpaket werden soll? Mathematisch folgt das aus der sogenannten Fouriertransformation. Der Effekt ist auch aus allen anderen Bereichen bekannt, die mit Wellen zu tun haben, beispielsweise aus der Nachrichtentechnik: Auch hier braucht man um die Trägerfrequenz herum ein Frequenzband, um der Trägerwelle ein weiteres längerwelliges Signal aufprägen zu können.
Ein einfaches Beispiel ist die Überlagerung zweier ebener Wellen mit fast gleicher Wellenlänge. Man spricht hier von einer Schwebung. Das Ergebnis sieht beispielsweise so aus:
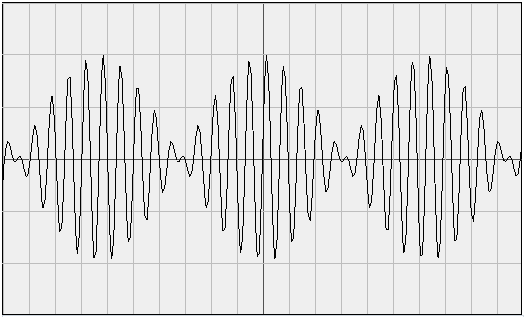
Man sieht, wie periodische Wellenpakete entstehen. Dabei sind diese Wellenpakete umso kleiner,
je weiter die beiden überlagerten Wellenlängen auseinander liegen.
Durch Überlagerung sehr vieler eng benachbarter Wellenlängen (genauer: eines kontinuierlichen Wellenlängenspektrums) kann man dafür sorgen, dass nur ein Wellenpaket übrig bleibt. Je breiter das überlagerte Wellenlängenspektrum ist, umso kleiner wird das Wellenpaket.
In der Quantenmechanik entspricht nun ein breites Wellenlängenspektrum einem großen Impulsspektrum, also einem breiten Bereich möglicher Impuls-Messwerte. Ein kleineres Wellenpaket entspricht im Gegenzug einem besser lokalisierten Teilchen, also einem kleineren Bereich möglicher Orts-Messwerte. Je größer das Impulsspektrum ist, umso kleiner ist das Wellenpaket und umgekehrt. Das ist der Inhalt der Heisenbergschen Unschärferelation.
Man findet manchmal das Argument, dass man bei einem endlichen Wellenpaket die Wellenlänge nur mit einer gewissen Ungenauigkeit bestimmen kann, und dass dies die Ursache für die Unschärferelation ist. Wenn wir uns die Grafik oben mit den zwei überlagerten Wellenlängen ansehen, so hat man zunächst allerdings den Eindruck, dass man im Bereich konstruktiver Interferenz (also großer Amplituden) durchaus eine Wellenlänge ermitteln kann. Diese ist in dem obigen Beispiel gerade der Mittelwert der beiden überlagerten Wellenlängen.
Allerdings ändert sich das im Bereich destruktiver Interferenz (sehr kleine Amplituden), denn dort erfolgt im obigen Beispiel eine Versetzung der Wellenberge um eine halbe Wellenlänge, wenn man zum nächsten Bereich großer Amplituden übergeht. Im Randbereich eines Wellenpaketes ist also die Wellenlänge nicht mehr so eindeutig ablesbar.
Wenn man im obigen Beispiel die Anzahl Wellenberge zwischen zwei destruktiven Bereichen zählt, so kommt es wegen der Versetzung im Bereich destruktiver Interferenz genau darauf an, wohin man die Grenze des Wellenpakets legt. Man kann in diesem Sinn auch sagen, dass die Anzahl Wellenberge (nennen wir sie \(n\)) zwischen zwei destruktiven Bereichen bestenfalls mit einer Genauigkeit von einem Wellenberg festgelegt ist: \[ \Delta n \gt 1 \] Ähnlich ist es auch bei der kontinuierlichen Überlagerung von vielen Wellen, die ein einziges Wellenpaket ergeben.
Nun ist die Wellenanzahl \(n\) in einem Wellenpaket ungefähr gleich \[ n = \frac{L}{\lambda} \] wobei \(L\) die Länge (Ausdehnung) des Wellenpaketes (also im obigen Beispiel die Strecke zwischen zwei Bereichen destruktiver Interferenz) und \lambda die mittlere Wellenlänge ist. Damit ist \[ \Delta n = \Delta \left(\frac{L}{\lambda}\right) = \frac{L}{\Delta \lambda} \] wenn wir \(L\) ohne Unsicherheit vorgeben.
In der Quantenmechanik ist nun \[ \lambda = \frac{h}{p} \] so dass \[ \Delta n = \frac{L}{\Delta \lambda} = \frac{L}{h} \, \Delta p \] ist. Die Größe \(L\) des Wellenpaketes gibt nun zugleich ungefähr die Ortsunsicherheit \(\Delta x\) des Teilchens an, so dass wir \[ h \, \Delta n = \Delta x \, \Delta p \] erhalten. Mit \( \Delta n \gt 1 \) folgt dann \[ \Delta x \, \Delta p = h \, \Delta n \gt h \] Diese Argumentation ist nicht allzu präzise, so dass Vorfaktoren wie 1/2 etc. hier nicht exakt zu erwarten sind. Sie vermittelt aber immerhin eine gewisse Veranschaulichung für die Unschärferelation, so dass ich hier nicht darauf verzichten wollte.
Neben der Unschärfe zwischen Ort und Impuls hatten wir auch die Unschärfe zwischen Energie und Zeit angesprochen. Da bei einer ebenen Welle das Produkt von Energie (Frequenz) und Zeit analog zum Produkt von Impuls (Wellenzahl) und Ort eingeht, ergeben die Überlagerungseigenschaften von Wellen auch eine analoge Unschärferelation.
Betrachtet man die Quantenmechanik etwas genauer, so entdeckt man allerdings Unterschiede zwischen den beiden Unschärferelationen. Ort und Impuls sind in der nichtrelativistischen Quantenmechanik beides Messgrößen (Observable), die sich bei einem Teilchen messen lassen, so dass die Unschärferelation sich auf die Streubreite der Messwerte bezieht.
Anders als der Ort ist aber die Zeit keine solchen Teilchen-Messgröße. Daher lässt sich in der Quantenmechanik die Energie-Zeit-Unschärferelation auch nicht analog zur Impuls-Orts-Unschärferelation streng formal ableiten. Was also ist mit der Zeitunschärfe \( \Delta t \) gemeint?
Es ist bemerkenswert, dass dazu im Lauf der Zeit immer wieder verschiedene Antworten gegeben und teilweise intensive Debatten geführt wurden. Daran merkt man, dass die Energie-Zeit-Unschärferelation keine so saubere formale Basis besitzt wie die Impuls-Orts-Unschärferelation.
Eine gängige Sichtweise ist diese:
Es gibt Beispiele, die diese Sichtweise unterstützen (z.B. die Ablenkung eines neutralen Teilchens mit Spin in einem Magnetfeld – das sogenannte Stern-Gerlach-Experiment), aber es gibt auch Gegenbeispiele (Bohm, Aharanov), so dass diese Sichtweise nicht konsistent überall durchgehalten werden kann.
Manchmal versucht man auch, die Energie-Zeit-Unschärfe auf die Energie-Impuls-Unschärfe zurückzuführen. Wir wollen hier gar nicht erst näher darauf eingehen, da diese Ableitung erhebliche Mängel aufweist.
Eine fruchtbare Sichtweise ergibt sich aus unserem obigen Bild eines Wellenpakets: Wir können die x-Achse entweder als Raumachse oder als Zeitachse interpretieren:
Die Zeitunschärfe \(\Delta t\) ist also hier die zeitliche Dauer des Wellenpaketes, also die Zeitdauer, während der die Amplitude an einem bestimmten Raumpunkt schwingt. Das Wellenpaket besteht dabei aus einem Bereich konstruktiver Interferenz (große Amplitude), der von Bereichen destruktiver Interferenz (kleine Amplitude) begrenzt wird, ganz analog zu unserem Beispiel oben.
Wie kann es nun zu einem zeitlich begrenzten Wellenpaket an einem Ort kommen? Dazu gibt es zwei Möglichkeiten:
Betrachten wir die beiden Fälle genauer:
Durchlaufzeit bzw. Veränderungszeit:
Man kann ganz allgemein für irgendeine Messgröße \(B\) und einen nichtstationären Quantenzustand \(\psi\) den folgenden Zusammenhang herleiten (Mandelstam, Tamm, 1945):
| \[ \frac{\Delta E \, \Delta B}{ \left| \frac{d \langle B \rangle }{dt} \right| } \gt \frac{\hbar}{2} \] |
Dabei ist \( \langle B \rangle \) der Erwartungswert (Mittelwert) und \( \Delta B \) die Standardabweichung (Streuung) der Messwerte, bezogen auf den Quantenzustand \(\psi\). Der Term \[ \Delta t := \frac{\Delta B}{ \left| \frac{d \langle B \rangle }{dt} \right| } \] ist dabei die Zeitspanne, innerhalb der sich der Mittelwert \( \langle B \rangle \) bei einer (als einigermaßen konstant angenommenen) Veränderungsgeschwindigkeit von \( \left| \frac{d \langle B \rangle }{dt} \right| \) gerade um eine Standardabweichung \( \Delta B \) verändern würde, da sich der zugehörige Quantenzustand \( \psi \) verändert hat, denn umgestellt ergibt die obige Gleichung \[ \Delta B = \left| \frac{d \langle B \rangle }{dt} \right| \, \Delta t \] In diesem Sinne ist \( \Delta t \) eine statistisch signifikante Veränderungszeit für den Quantenzustand, bestimmt über die Messgröße \(B\), und für diese Veränderungszeit gilt die Unschärferelation: Ein Quantenzustand mit nur einem kleinen überlagerten Energiebereich \(\Delta E\) ist sehr stabil, d.h. jede Messgröße \(B\) hat dann eine Veränderungszeit \(\Delta t\), die größer als \( (\hbar/2) (1/\Delta E) \) ist.
Konkret können wir als Messgröße \(B\) den Teilchenort \(x\) wählen und erhalten \[ \Delta t = \frac{\Delta x}{ \left| \frac{d \langle x \rangle }{dt} \right| } \] Das reproduziert unsere Interpretation von \(\Delta t\) als Durchlaufzeit, während der das Wellenpaket mit Größe \(\Delta x\) sich mit der Geschwindigkeit \( \left| \frac{d \langle x \rangle }{dt} \right| \) an einem bestimmten Ort vorbeibewegt.
mittlere Lebensdauer:
Dieser Fall ist in der Quantentheorie besonders wichtig, und er kann auch beispielsweise im Rahmen der quantenmechanischen Streutheorie mathematisch sauber behandelt werden. Dabei hat man es mit einem Prozess zu tun, bei dem ein bestimmter (instabiler) Quanten-Zwischenzustand vorübergehend aktiviert wird, um dann wieder zu verschwinden. So könnte aus anderen Quantenzuständen Energie auf den betrachteten Zwischenzustand übertragen werden, worauf dieser seine Energie dann wieder an andere Quantenzustände abgibt.
Beispielsweise können Photonen ihre Energie an ein Atom übertragen und dort einen höheren Energiezustand anregen, der seine Energie dann mit einer gewissen Wahrscheinlichkeit wieder in Form von Photonen abstrahlt, oder es kann aus einem hochenergetischen Elektron-Positron-Paar ein Z-Boson gebildet werden, das anschließend wieder zerfällt.
In diesem Sinn entspricht die zeitliche Dauer \(\Delta t\) des Wellenpaketes ungefähr der mittleren Lebensdauer des angeregten Quantenzustandes, und die Energieunschärfe \(\Delta E\) entspricht der natürlichen Linienbreite einer Spektrallinie oder der Resonanzbreite in einer Teilchen-Erzeugungsrate (siehe auch Kapitel 6.2).
Der Energieerhaltungssatz wird durch die Energie-Zeit-Unschärfe dabei nicht verletzt, auch nicht für kurze Zeiten. Es wird auch keine Energie kurzzeitig geborgt.
Stattdessen ist es einfach nur so, dass ein kurzlebiger Quantenzustand immer aus einer Überlagerung mehrerer Energiewerte besteht, die alle als ununterscheidbare Möglichkeiten zum betrachteten Prozess beitragen können, je nach Randbedingung. Ein Atom kann von einem Grundzustand aus durch ein Photon in einen angeregten Energiezustand überführt werden und diesen durch Aussenden eines Photons gleicher Energie wieder verlassen. Aufgrund der Kurzlebigkeit des angeregten Energiezustandes ist dieser Prozess dabei für einen ganzen Photon-Energiebereich möglich, der der natürlichen Linienbreite der zugehörigen Spektrallinie entspricht. Analog ist es bei Erzeugung und Zerfall des Z-Bosons.
Das zentrale Argument für den Zusammenhang zwischen mittlerer Lebensdauer und Resonanzbreite sieht dabei folgendermaßen aus (dieses Argument ist letztlich auch der zentrale Kern anderer aufwendigerer Herleitungen im Rahmen der Streutheorie):
Wir bezeichnen mit \( \psi(t) \) die Wahrscheinlichkeitsamplitude dafür, dass wir bei einer Messung zur Zeit \(t\) den kurzlebigen Zustand (z.B. das Z-Boson) vorfinden.
Dabei wollen wir uns vorstellen, dass der Zustand zur Zeit \( t = 0 \) plötzlich mit gewisser Wahrscheinlichkeit aktiviert wird und danach so zerfällt, dass sich das übliche exponentielle Zerfallsgesetz mit der mittleren Lebensdauer \(\tau\) ergibt (Vorsicht: das ist eine Näherung, die auf bestimmten Annahmen beruht – mehr dazu in Norbert Dragon: Anmerkungen zur Quantenmechanik, Kapitel 7: Zerfall eines instabilen Teilchens).
Der Zustand soll eine mittlere Energie \(E_{0}\) aufweisen, und er soll so langsam zerfallen, dass seine mittlere Lebensdauer \(\tau\) deutlich größer als seine Schwingungsperiode \( T = h/E_{0} \) ist. Nur so macht es überhaupt Sinn, von einer Linie oder Resonanz zu sprechen, wie wir unten noch sehen werden. Dann weist die folgende Amplitude die gewünschten Eigenschaften auf:
| \[ \psi(t) = A \, e^{- \frac{i}{\hbar} E_{0} t } \, e^{- \frac{t}{2 \tau}} \] |
Dabei gilt wie gefordert \[ |\psi(t)|^{2} = e^{- \frac{t}{\tau}} \] (exponentielles Zerfallsgesetz) und die Welle schwingt mit der Frequenz \[ f = \frac{E_{0}}{\hbar} \]
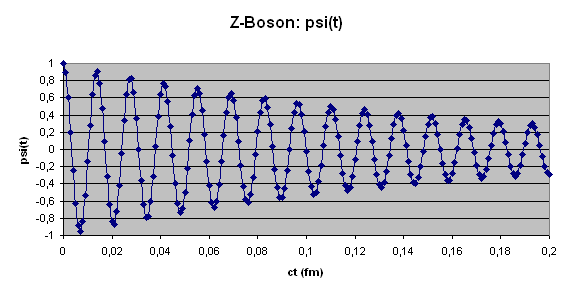
Realteil der Zeitamplitude \(\psi(t)\) für ein Z-Boson
(Masse \(E_{0} = 91,2\) GeV, Breite \(\Gamma = 2,5\) GeV).
Auf der x-Achse ist die Zeit als entsprechender Lichtweg \( c t \) in Fermi angegeben.
Die mittlere Lebensdauer entspricht dabei einem Lichtweg von
\( c \tau = c \hbar / \Gamma = 0,2 \, \mathrm{GeV} \, \mathrm{fm} / 2,5 \, \mathrm{GeV} = 0,08 \, \mathrm{fm} \).
Das Z-Boson ist also sehr instabil und zerfällt praktisch noch an seinem Entstehungsort.
Da bei der Schwingung die Amplitude ständig abnimmt, ist \(E_{0}\) nicht die einzige Energie,
die hier eine Rolle spielt – es handelt sich letztlich wie oben um ein zeitliches Wellenpaket,
und wir können \(\psi(t)\) als Überlagerung vieler Schwingungen
\( a(E) \, e^{- \frac{i}{\hbar} E t } \) mit jeweils scharfer Energie \(E\) schreiben:
\[
\psi(t) = \int dE \, a(E) \, e^{- \frac{i}{\hbar} E t }
\]
Das ist eine Fouriertransformation, so dass umgekehrt für die Energieamplitude \(a(E)\) gilt:
\[
a(E) = \frac{1}{2 \pi \hbar} \, \int_0^\infty dt \, \psi(t) \, e^{\frac{i}{\hbar} E t }
\]
Dabei geht das Integral von \( t = 0 \) bis Unendlich, da \(\psi(t)\) bei kleineren Zeiten Null ist.
Dieses Integral können wir direkt ausrechnen:
\[
a(E) =
\frac{1}{2 \pi \hbar} \, \int_0^\infty dt \, \psi(t) \, e^{\frac{i}{\hbar} E t }
=
\]
\[
=
\frac{1}{2 \pi \hbar} \, \int_0^\infty dt \,
A \,
e^{- \frac{i}{\hbar} E_{0} t } \, e^{- \frac{t}{2 \tau}}
\,
e^{\frac{i}{\hbar} E t }
=
\]
\[
=
\frac{A}{2 \pi \hbar} \, \int_0^\infty dt \,
e^{ \left( \frac{i}{\hbar} \, (E - E_{0}) - \frac{1}{2 \tau} \right) \, t}
=
\]
\[
=
\frac{A}{2 \pi \hbar} \,
\frac{ 1 }{ \frac{i}{\hbar} \, (E - E_{0}) - \frac{1}{2 \tau} }
\,
e^{ \left( \frac{i}{\hbar} \, (E - E_{0}) - \frac{1}{2 \tau} \right) \, t}
\bigg|^{\infty}_{0}
=
\]
\[
=
- \frac{A}{2 \pi \hbar} \,
\frac{ 1 }{ \frac{i}{\hbar} \, (E - E_{0}) - \frac{1}{2 \tau} }
=
\]
\[
= - \frac{A}{2 \pi} \,
\frac{ 1 }{ i \, (E - E_{0}) - \frac{\hbar}{2 \tau} }
\]
Die Wahrscheinlichkeit, bei dem durch \( \psi(t) \) beschriebenen Zustand die Energie \(E\) zu messen,
ist damit proportional zu
\[
|a(E)|^{2} = a(E) \, a(E)^{*}
=
\]
\[ =
\frac{A^2}{(2 \pi)^2} \,
\frac{ 1 }{ (E - E_{0})^{2} + \left(\frac{\hbar}{2 \tau}\right)^{2} }
\]
Bis auf den Vorfaktor tritt also bei einem instabilen Zustand mit mittlerer Lebensdauer \(\tau\)
die Energie \(E\) mit der Wahrscheinlichkeit
\[
\frac{ 1 }{ (E - E_{0})^{2} + \left(\frac{\hbar}{2 \tau}\right)^{2} }
\]
auf, sofern \(\tau\) groß genug ist (d.h. sofern \( \hbar/(2\tau) \) deutlich kleiner als \(E_{0}\) ist).
Diese Wahrscheinlichkeit hat bei \( E = E_{0} \) ihr Maximum
und fällt zu beiden Seiten hin ab, wobei sie sich bei
\( E - E_{0} = \hbar/(2\tau) \) gerade halbiert.
Den Term
| \[ \Gamma := \frac{\hbar}{\tau} \] |
bezeichnet man dabei als natürliche Linienbreite (bei Spektrallinien) oder als Resonanzbreite (bei Teilchenstreuung), d.h. die Wahrscheinlichkeit für \(E\) ist proportional zu \[ \frac{ 1 }{ (E - E_{0})^{2} + \left(\frac{\Gamma}{2}\right)^{2} } \] Diese Funktion trägt den Namen Breit-Wigner-Kurve oder auch Lorentz-Kurve:
| Breit-Wigner-Kurve (Lorentz-Kurve): \[ \frac{ 1 }{ (E - E_{0})^{2} + \left(\frac{\Gamma}{2}\right)^{2} } \] |
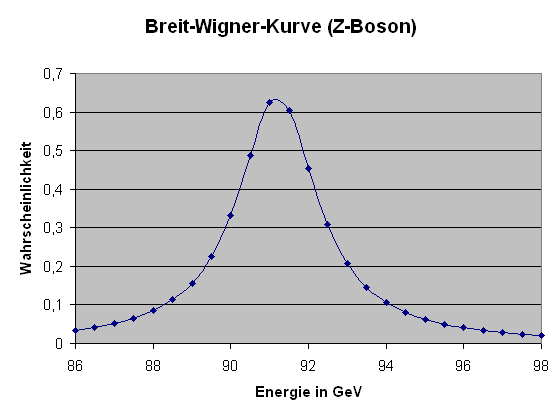
Berechnete Breit-Wigner-Kurve (ohne Normierung) für ein
Z-Boson (Masse \(E_{0} = 91,2\) GeV, Breite \(\Gamma = 2,5\) GeV).
Anschaulich ist \(\Gamma\) dabei die Breite der Resonanz zwischen den beiden Energien, bei denen
sich der maximale Funktionswert halbiert hat.
Genau diese Formel werden wir in Kapitel 6.2
beim Aufspüren des Z-Bosons wiederfinden,
das als kurzlebige Resonanz beispielsweise bei der Elektron-Positron-Kollision auftritt.
Den Zusammenhang zur Energie-Zeit-Unschärfe erhalten wir dabei zurück, indem wir \( \Gamma = \Delta E \) als Breite des zu überlagernden Energieintervalls und \( \tau = \Delta t \) als ein Maß für die zeitliche Ausdehnung des Wellenpakets betrachten. Die Formel \( \Gamma = \hbar / \tau \) entspricht dann der Energie-Zeit-Unschärfe \( \Delta E \, \Delta t = \hbar \).
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 27 December 2023