Aus dem letzten Kapitel (Kapitel 5.2 Das Einsteinsche Äquivalenzprinzip) wissen wir, dass in der allgemeinen Relativitätstheorie lokal kein Unterschied zwischen einem beschleunigten Bezugssystem und einer Gravitationswirkung besteht. Daher kann man lokal auch immer ein frei fallendes Bezugssystem finden, in dem man die Gravitation nicht spürt.
Aber: Weit entfernte Objekte nehmen wir in einem Gravitationsfeld zumeist als beschleunigt wahr, auch wenn wir uns selber im freien Fall befinden. Ein Beispiel sind zwei Satelliten, die auf verschiedenen Bahnen die Erde umkreisen. In jedem Satellit spürt man keine Gravitation, aber der jeweils andere Satellit erscheint den schwerelosen Insaßen des einen Satelliten als beschleunigt (d.h. er bewegt sich nicht auf einer geradlinig-gleichförmigen Bahn im Bezugssystem des einen Satelliten).
Die Unmöglichkeit, ein globales Bezugssystem zu finden, in dem sich alle frei fallenden Objekte unbeschleunigt zueinander bewegen, ist daher in der allgemeinen Relativitätstheorie die kennzeichnende Eigenschaft von Gravitation. Mathematisch verhindert die Gravitation, dass man global die Raumzeit mit karthesischen Koordinaten und Minkowski-Metrik beschreiben kann. Aus der Differentialgeometrie weiß man, dass dies genau dann unmöglich ist, wenn der Riemannsche Krümmungstensor ungleich Null ist:
Was ist die Ursache für diese nicht-verschwindende Krümmung der Raumzeit?
Im Newtonschen Gravitationsgesetz entsteht Gravitation durch die Anwesenheit von Masse. Man muss also versuchen, das Newtonsche Gravitationsgesetz durch eine koordinaten-unabhängige (tensorielle) Beziehung zwischen Materie und Raum-Zeit-Krümmung zu verallgemeinern, so dass sich im nichtrelativistischen Grenzfall wieder das Newtonsche Gravitationsgesetz ergibt.
Es ist keineswegs einfach, diese Verallgemeinerung zu finden, und auch Einstein hat dafür einige Zeit benötigt. So erinnert sich Einstein im Juni 1933 an die Jahre vor 1915:
Aber das ahnungsvolle, Jahre währende Suchen im Dunkeln mit seiner gespannten Sehnsucht, seiner Abwechslung von Zuversicht und Ermattung und seinem endlichen Durchbrechen zur Klarheit, das kennt nur, wer es selber erlebt hat.
Man kann das verallgemeinerte Gravitationsgesetz nicht streng ableiten oder beweisen, sondern man kann nur intelligent raten, wie es aussehen sollte, und dann die physikalischen Konsequenzen des gefundenen Gesetzes untersuchen und letztlich im Experiment verifizieren. Die folgende Darstellung orientiert sich u.a. an Kapitel 4 Einstein field equations in Matt Visser: notes on general relativity, Math 465, im Folgenden mit [MV] abgekürzt (ich konnte den Text leider im Internet nicht mehr wiederfinden). Die Rechnungen werde ich dabei nicht im Detail hier wiederholen, sondern ggf. kurz inhaltlich zusammenfassen.
Das Newtonsche Gravitationsgesetz für das Gravitationspotential \(\phi\) lautet für eine Massendichte \(\rho\) allgemein \[ \mathrm{div} \, (\mathrm{grad} \, \phi) = 4 \pi G_{N} \, \rho \] mit der Gravitationskonstante \(G_{N}\) (das tiefergestellte \(N\) steht für Newton und dient zur Unterscheidung vom Einstein-Tensor \(G\), den wir bald benötigen).
Bei einer punktförmigen Materieansammlung der Gesamtmasse \(M\) im Koordinaten-Nullpunkt ergibt sich nach dem Integralsatz von Stokes bei Integration über ein Kugelvolumen \(B(r)\) mit Radius \(r\) bzw. Integration über die Kugeloberfläche \(\delta B(r)\) dann für die linke Seite Folgendes: \[ \int_{B(r)} \, \mathrm{div} \, (\mathrm{grad} \, \phi) \, dV = \] \[ = \int_{\delta B(r)} \, (\mathrm{grad} \, \phi) \, \boldsymbol{dA} = \] \[ = |\mathrm{grad} \, \phi| \, 4\pi r^{2} \] Für die rechte Seite erhalten wir \[ \int_{B(r)} \, 4 \pi G_{N} \, \rho \, dV =: 4 \pi G_{N} \, M \] Vergleich beider Seiten ergibt: \[ |\mathrm{grad} \, \phi| = G_{N} \frac{M}{r^{2}} \] und mit \( \mathrm{grad} \, \phi = - \boldsymbol{F}/m \) somit das bekannte Newtonsche Gravitationsgesetz.
Wie kann man nun versuchen, die obige nichtrelativistische Gleichung \[ \mathrm{div} \, (\mathrm{grad} \, \phi) = 4 \pi G_{N} \, \rho \] (also das Newtonsche Gravitationsgesetz) relativistisch zu verallgemeinern?
Bei der beschleunigten Rakete hatten wir gesehen, dass die Gravitationsbeschleunigung (also klassisch die Gravitationskraft) durch das Christoffelsymbol \( \Gamma^{3}_{00} \) entsteht, wenn die Rakete in \(x^3\)-Richtung beschleunigt (siehe Kapitel 5.2 Das Einsteinsche Äquivalenzprinzip ).
Das lässt sich auch ganz allgemein für die Beschleunigung eines zuvor ruhenden Objektes zeigen (siehe [MV] Kapitel 3.3). Also muss im nichtrelativistischen Grenzfall \( \Gamma^{i}_{00} \) proportional zur klassischen Gravitationsbeschleunigung \( (\mathrm{grad} \, \phi)^{i} \) sein.
Das Newtonsche Gravitationsgesetz enthält nun wiederum zweite Ableitungen des Gravitationspotentials \( \phi \), was ersten Ableitungen der Christoffelsymbole entspricht. Die linke Seite \( \mathrm{div} \, (\mathrm{grad} \, \phi) \) wird beim verallgemeinerten Gravitationsgesetzes also vermutlich Christoffelsymbole (wollen wir nicht ausschließen) und erste Ableitungen dieser Symbole enthalten. Welche koordinatenunabhängigen Objekte (Tensoren), die sich so bilden lassen, kommen für das verallgemeinerte Gravitationsgesetz in Frage?
Zur Klärung dieser Frage ist es nützlich, sich zunächst Raumbereiche anzusehen, in denen sich keine Materie oder irgendwelche Energieformen (z.B. Licht) befinden. Das bedeutet nicht, dass in diesen Raumbereichen keine Gravitation herrscht, denn die gravitationserzeugende Materie kann sich ja außerhalb des betrachteten Raumbereichs befinden. So könnten wir uns beispielsweise für den materiefreien Raum um einen Stern herum interessieren (zumindest wollen wir ihn als weitgehend materiefrei ansehen).
Das Newtonsche Gravitationsgesetz für leere Raumbereiche lautet \[ \mathrm{div} \, (\mathrm{grad} \, \phi) = 0 \] Wir suchen nun einen geeigneten Tensor, der erste Ableitungen der Christoffelsymbole enthält und der an die Stelle der linken Seite dieser Gleichung tritt (der also für leere Raumbereiche gleich Null ist). Zum Glück gibt es nicht allzuviele Kandidaten, denn die Bedingung, dass ein Tensor entstehen muss (der in Koordinatendarstellung das entsprechende Transformationsverhalten bei Koordinatenwechseln aufweisen muss), schränkt die Kombinationsmöglichkeiten erheblich ein. Schauen wir uns die Kandidaten der Reihe nach an:
Den Riemannschen Krümmungstensor hatten wir in Krümmung bereits ausführlich diskutiert. Hier eine kurze Wiederholung:
Der Riemannsche Krümmungstensor \[ R^{\mu}_{\;\nu\rho\sigma} \] kann koordinatenfrei als Abbildung \( R(u,v) \) definiert werden, so dass der Ausdruck \[ R(u,v) \, w \] ein Tangentialvektor ist. Dabei gibt \( R(u,v) \, w \) (geeignet normiert) an, wie sich der Tangentialvektor \(w\) verändert, wenn er entlang eines durch \(u\) und \(v\) aufgespannten infinitesimalen Rechtecks im Kreis paralleltransportiert wird. In Komponenten ausgeschrieben ist \[ [R(u,v) \, w]^{\mu} = \] \[ = \sum_{\;\nu\rho\sigma} \, R^{\mu}_{\;\nu\rho\sigma} \, w^{\nu} u^{\rho} v^{\sigma} \] und es gilt \[ R^{\mu}_{\;\nu\rho\sigma} = \frac{\partial \Gamma^{ \mu}_{\sigma\nu}}{\partial x^{\rho}} - \frac{\partial \Gamma^{ \mu}_{\rho\nu}}{\partial x^{\sigma}} + \] \[ + \sum_{\alpha} \, \left( \Gamma^{ \mu}_{\rho\alpha} \Gamma^{ \alpha}_{\sigma\nu} - \Gamma^{ \mu}_{\sigma\alpha} \Gamma^{ \alpha}_{\rho\nu} \right) \] d.h. der Krümmungstensor enthält wie gewünscht erste Ableitungen der Christoffelsymbole. Man erkennt, dass \( R^{\mu}_{\;\nu\rho\sigma} \) antisymmetrisch in den letzten beiden Indices ist.
Ist dieser Tensor ein geeigneter Kandidat, den wir in materiefreien Raumbereichen gleich Null setzen können, auch wenn Gravitation vorliegt?
Aus dem letzten Kapitel wissen wir, dass dies bedeuten würde, dass sich überall im materiefreien Raumbereich ein einziges Inertialsystem einführen ließe, so dass in dem Raumbereich keinerlei Gravitation herrschen würde. Die Christoffelsymbole wären in diesem Koordinatensystem alle im gesamten materiefreien Raumbereich gleich Null. Das würde viel zu weit gehen, denn wir könnten beispielsweise die Gravitation im leeren Raum um einen Stern herum nicht beschreiben. Der Riemannsche Krümmungstensor ist also kein geeigneter Kandidat für das verallgemeinerte Gravitationsgesetz!
Den Ricci-Tensor hatten wir bereits am Ende des letzten Kapitels kennengelernt. Man gewinnt ihn aus dem Riemannschen Krümmungstensor durch Kontraktion des ersten mit dem dritten Index: \[ R_{\nu\sigma} := \sum_{\mu} \, R^{\mu}_{\;\nu\mu\sigma} \] Entsprechend schreiben wir \[ \mathrm{Ric}(w,v) := \sum_{\nu\sigma} \, R_{\nu\sigma} w^{\nu} v^{\sigma} \] Dieser Ausdruck hängt nicht vom Koordinatensystem ab. Im letzten Kapitel hatten wir deshalb auch die folgende koordinatenfreie Formulierung kennengelernt: \[ \mathrm{Ric}(w,v) := \mathrm{Spur} ( R(\;,v) w ) \] Ohne Torsion (was in unserem Fall zutrifft) ist der Ricci-Tensor symmetrisch (analog zur Metrik). In 2 und 3 Dimensionen reicht der Ricci-Tensor zur Beschreibung der Krümmung vollständig aus. In 4 Dimensionen (also auch in der Raumzeit) benötigt man zur vollständigen Charakterisierung der Krümmung allerdings den Riemannschen Krümmungstensor von oben. Und genau das ist hier von Vorteil, denn in der vierdimensionalen Raumzeit ist demnach der Krümmungstensor durch den Ricci-Tensor nicht eindeutig festgelegt.
Wenn wir also für materiefreie Raumbereiche \( R_{\nu\sigma} = 0 \) fordern würden, so kann die Krümmung dennoch ungleich Null sein und Gravitation könnte damit auch in materiefreien Raumbereichen durch eine nicht-verschwindende Krümmung beschrieben werden. Daher kommt der Ricci-Tensor als Kandidat für das verallgemeinerte Gravitationsgesetz in Frage.
Man kann sich natürlich fragen, warum man oben ausgerechnet den ersten mit dem dritten Index im Riemannschen Krümmungstensor kontrahiert.
Wegen der Antisymmetrie in den letzten beiden Indices hätte man auch den ersten mit dem vierten Index kontrahieren können. Das Ergebnis wäre der Ricci-Tensor mit negativem Vorzeichen, also nichts wesentlich Neues.
Man hätte auch den ersten mit dem zweiten Index kontrahieren können: \[ S_{\rho\sigma} := \sum_{\mu} \, R^{\mu}_{\;\mu\rho\sigma} \] Dieser Tensor ist in der allgemeinen Relativitätstheorie gleich Null (siehe [MV2] Kapitel 3.6 Riemann curvature S.58) und spielt daher keine Rolle. So ist es offenbar auch mit anderen Kontraktionen: Aufgrund der Symmetrien des Riemannschen Krümmungstensors (Bianchi-Identitäten etc.) sind sie entweder Null oder im Wesentlichen gleich dem Ricci-Tensor.
Aufgrund der Symmetrien hat der Riemannsche Krümmungstensor in 4 Dimensionen nur 20 unabhängige Komponenten. Davon kann man 10 unabhängige Komponenten dem obigen Ricci-Tensor zuordnen. Die anderen 10 unabhängigen Komponenten wiederum kann man dem sogenannten Weyl-Tensor zuordnen (siehe [MV2] Kapitel 6.8 The Weyl tensor – Details lasse ich hier weg). Man könnte also alternativ zum Ricci-Tensor auch den Weyl-Tensor als Kandidaten für das verallgemeinerte Gravitationsgesetz in Betracht ziehen. Auch hier könnte man in materiefreien Raumbereichen diesen Tensor gleich Null setzen und behielte noch Freiheitsgrade im Krümmungstensor, um die Gravitation in diesem Raumbereich zu beschreiben. Dies wurde im Rahmen von Nordstroms konform-flachen Modell in den Jahren bis etwa 1920 tatsächlich auch versucht.
Der Weyl-Tensor hat nun eine charakteristische Eigenschaft: Führt man eine konforme Transformation der Koordinaten durch (d.h. in neuen Koordinaten ist die metrische Matrix gleich der alten metrischen Matrix mal einer positiven Konstanten \(\Omega^{2}\)), so ist auch der Weyl-Tensor in neuen Koordinaten gleich dem Weyl-Tensor in alten Koordinaten multipliziert mit \(\Omega^{2}\).
Man kann nun zeigen: Wenn der Weyl-Tensor in einem Raumbereich gleich Null ist, so ist der Raum dort konform-flach, d.h. die Metrik ist gleich der Minkowski-Metrik, multipliziert mit \(\Omega^{2}\).
Nun werden Lichtstrahlen durch Geodäten dargestellt, bei denen der Tangentialvektor \(u\) überall Metrik gleich Null hat: \(g(u,u) = 0\) (man spricht deshalb auch von Null-Geodäten). Diese Aussage ändert sich auch durch Umparametrisierungen nicht. Der Kurvenparameter ist bei solchen lichtartigen Kurven natürlich nicht gleich der Eigenzeit, da diese für diese Kurven nicht definiert ist – Licht altert nicht!
Man kann nun zeigen, dass in konform-flachen Räumen die Null-Geodäten (also Lichtstrahlen) genauso außehen wie im Minkowskiraum der speziellen Relativitätstheorie, d.h. es gibt keine Lichtablenkung durch die Gravitation. Das aber widerspricht den experimentellen Resultaten, d.h. Nordstroms konform-flaches Modell und damit der Weyl-Tensor scheiden als Kandidaten für das verallgemeinerte Gravitationsgesetz aus!. Man sieht, wie komplex die Sache im Detail ist und welche Möglichkeiten es gibt. Einsteins verallgemeinertes Gravitationsgesetz liegt also keineswegs wie selbstverständlich auf der Hand. Kein Wunder, dass es auch Einstein nicht leicht fiel, es zu finden.
Auch den Ricci-Skalar hatten wir am Ende des letzten Kapitels bereits kennengelernt. Mit Hilfe der inversen metrischen Matrix kann man nämlich die Spur über die Indices des Ricci-Tensors bilden und so den Ricci-Skalar (auch skalare Krümmung genannt) definieren: \[ R := \sum_{\nu\sigma} \, g^{\nu\sigma} \, R_{\nu\sigma} =: \mathrm{Spur}_{g} ( \mathrm{Ric} ) \] wobei das kleine \(g\) bei der Spur unten andeutet, dass vor der Spurbildung der erste Index mit der Metrik hochgezogen wird. Für die Definition des Ricci-Skalars benötigt man also eine Metrik! Der Ausdruck für \(R\) hängt nicht vom Koordinatensystem ab. In 2 Dimensionen (also bei Flächen) reicht der Ricci-Skalar zur Beschreibung der Krümmung vollständig aus, aber nicht mehr in 3 Dimensionen.
In materiefreien Raumbereichen wäre dann der Ricci-Skalar gleich Null zu setzen. Das würde jedoch für den Krümmungstensor noch sehr viele Freiheiten bedeuten und führt zu sehr merkwürdigen Lösungen für die Raum-Zeit-Geometrie der materiefreien (aber nicht gravitationsfreien) Raumzeit ([MV] erwähnt z.B. sogenannte traversable wormhole solutions). Solche Lösungen sind nicht möglich, wenn wir den Ricci-Tensor gleich Null setzen.
Fazit:
Wenn man sich die verschiedenen Möglichkeiten ansieht, so gelangt man zu dem
Schluss, dass der Ricci-Tensor am geeignetsten erscheint,
um die linke Seite des Newtonschen Gravitationsgesetzes
\[
\mathrm{div} \, ( \mathrm{grad} \, \phi ) = 4 \pi G_{N} \, \rho
\]
zu verallgemeinern. Im materiefreien Raum wäre dann
den Ricci-Tensor gleich Null, was genau das richtige Maß an Freiheit für
den Krümmungstensor erlaubt. Weiter unten werden wir sehen, dass wir damit fast richtig,
aber dennoch nicht ganz richtig geraten haben. Mehr dazu später.
Kommen wir zur rechten Seite des Newtonschen Gravitationsgesetzes \[ \mathrm{div} \, ( \mathrm{grad} \, \phi ) = 4 \pi G_{N} \, \rho \] Wie können wir die Materiedichte \(\rho\) so verallgemeinern, dass sich eine sinnvolle tensorielle Gleichung ergibt?
Eine sehr schöne Darstellung dazu habe ich in [MV] Kapitel 4.3 ff. gefunden:
Gravitation beschreibt in der allgemeinen Relativitätstheorie die Tatsache, dass man kein großräumiges Inertialsystem einführen kann, in dem sich alle frei fallenden Objekte unbeschleunigt bewegen. Es liegt daher nahe, sich die Bewegung zweier frei fallender Körper anzusehen und zu untersuchen, wie die Flugbahnen auseinander laufen. Um die Diskussion einfach zu halten, nehmen wir an, dass die beiden Körper sehr dicht beieinander starten.
In der Newtonschen Physik sieht das Ganze dann so aus:
Zwei frei fallende Teilchen (oder sonstige Objekte) bewegen sich auf zwei eng benachbarten
Flugbahnen \(\boldsymbol{x}(t)\) und \(\boldsymbol{y}(t)\). Es gelten im Gravitationspotential \(\phi\)
die Bewegungsgleichungen
\[
\frac{d^{2}}{dt^{2}} \boldsymbol{x}(t) = - \mathrm{grad} \, \phi(\boldsymbol{x}(t))
\]
\[
\frac{d^{2}}{dt^{2}} \boldsymbol{y}(t) = - \mathrm{grad} \, \phi(\boldsymbol{y}(t))
\]
Wir wollen dabei annehmen, dass die beiden Teilchen so leicht sind, dass die Gravitation zwischen ihnen
keine Rolle spielt. Nur das äußere Gravitationspotential soll ihre freie Fallbewegung steuern.
Stellen Sie sich gerne zwei Satelliten auf eng benachbarten Flugbahnen vor, die die Erde umkreisen.
Der kleine Abstand \[ \boldsymbol{dx}(t) = \boldsymbol{y}(t) - \boldsymbol{x}(t) \] zwischen den beiden Teilchen entwickelt sich demnach im Gravitationspotential zeitlich so: \[ \frac{d^{2}}{dt^{2}} \boldsymbol{dx}(t) = \] \[ = \frac{d^{2}}{dt^{2}} ( \boldsymbol{y}(t) - \boldsymbol{x}(t) ) = \] \[ = - \mathrm{grad} \, ( \phi(\boldsymbol{y}(t)) - \phi(\boldsymbol{x}(t)) ) = \] \[ = - \mathrm{grad} \, \left( \, (\mathrm{grad} \, \phi(\boldsymbol{x}(t)) \, \boldsymbol{dx}(t)) + \, ... \right) \] wobei wir bei den eng benachbarten Teilchen in erster Ordnung die Näherung \[ \phi(\boldsymbol{y}(t)) - \phi(\boldsymbol{x}(t)) = \] \[ = (\mathrm{grad} \, \phi(\boldsymbol{x}(t)) \, \boldsymbol{dx}(t)) + \, ... \] verwendet haben.
Wenn wir unser Ergebnis in Komponenten ausschreiben und damei die Abkürzung \[ K^{i}_{\;j} := \frac{\partial^{2}\phi}{\partial x^{i} \, \partial x^{ j}} \] verwenden, so haben wir: \[ \frac{d^{2}}{dt^{2}} \, dx^{i}(t) = - \sum_{j} \, K^{i}_{\;j} \, dx^{ j}(t) + \, ... \] Andererseits ist \[ \mathrm{Spur} (K) = \sum_{i} \, K^{i}_{\;i} = \sum_{i} \, \frac{\partial ^{2}\phi}{(\partial x^{i})^{2}} = \] \[ = \mathrm{div} \, (\mathrm{grad} \, \phi) = 4 \pi G_{N} \, \rho \] Diese Gleichung verbindet also den Gezeitenkräfte-Tensor \(K\) mit der Anwesenheit von Materie in der Newtonschen Gravitationstheorie.

Analog kann man auch in der allgemeinen Relativitätstheorie vorgehen.
An die Stelle der obigen Bewegungsgleichungen treten die Geodätengleichungen mit den
Christoffelsymbolen. Nach längerer Rechnung (siehe [MV] Kapitel 4.4) ergibt sich:
\[
\frac{d^{2}}{d\tau^{2}} \, dx^{\mu}(\tau) =
- \sum_{\sigma} \, K^{\mu}_{ \;\sigma} \,
dx^{\sigma}(\tau) + \, ...
\]
mit
\[
K^{\mu}_{\;\sigma} :=
- \sum_{\nu\rho} \,
R^{\mu}_{\;\nu\rho\sigma} \, u^{\nu} u^{\rho}
\]
wobei \(u\) der Tangentialvektor (Vierer-Geschwindigkeitsvektor) der Bewegung eines der Teilchen ist
(egal welches, da sie auf sehr ähnlichen Flugbahnen fliegen sollen) und \(\tau\) entsprechend die
zugehörige Eigenzeit ist.
[MV] bezeichnet die obige Gleichung auch als equation of geodesic deviation. Man sieht schön, dass der Krümmungstensor hier die Ursache für das Auseinanderlaufen der Geodäten ist. In John Baez, Emory Bunn: The Meaning of Einstein's Equation (auch unter arXiv:gr-qc/0103044), wird diese Gleichung ebenfalls hergeleitet, allerdings direkt (ohne lange Rechnung) mit Hilfe der geometrischen Definition des Krümmungstensors durch Parallelverschiebung entlang eines infinitesimalen Rechtecks (siehe oben sowie Krümmung).
Die relativistische Gleichung sieht ganz analog zur Gleichung der Newtonschen Physik aus. Sie sollte im nichtrelativistischen Grenzfall bei schwacher Gravitation in letztere übergehen (die metrische Matrix, speziell \(g_{00}\) liefert dabei das Analogon zum Potential \(\phi\)). Das sieht schon mal gut aus.
Was uns aber noch fehlt, ist das relativistische Analogon zur nichtrelativistischen Gleichung \[ \mathrm{Spur} (K) = 4 \pi G_{N} \, \rho \] die das Newtonsche Gravitationsgesetz beschreibt. Wir wollen daher für das relativistische Analogon den folgenden Ansatz machen: \[ \mathrm{Spur} (K) = 4 \pi G_{N} \, \rho(u) \] Dabei ist \(\rho(u)\) die relativistisch verallgemeinerte Materiedichte, wie sie ein Beobachter messen würde, der sich mit Vierergeschwindigkeit \(u\) bewegt – was das bedeuten soll, müssen wir uns gleich noch überlegen.
Die linke Seite können wir schon mal ausrechnen (wobei wir die Antisymmetrie des Krümmungstensors in den letzten beiden Indices verwenden): \[ \mathrm{Spur} (K) = \] \[ = - \sum_{\mu\nu\rho} \, R^{\mu}_{\;\nu\rho\mu} \, u^{\nu} u^{\rho} = \] \[ = \sum_{\mu\nu\rho} \, R^{\mu}_{\;\nu\mu\rho} \, u^{\nu} u^{\rho} = \] \[ = \sum_{\nu\rho} \, R_{\nu\rho} \, u^{\nu} u^{\rho} = \] \[ = \mathrm{Ric}(u,u) \] so dass unser Ansatz für ein verallgemeinertes Gravitationsgesetz lautet: \[ \mathrm{Ric}(u,u) = 4 \pi G_{N} \, \rho(u) \] Das passt sehr gut zu unserer Überlegung weiter oben, in der wir den Ricci-Tensor für materiefreie Raumbereiche gleich Null setzen wollten. Genau das erhalten wir, wenn wir in unserem Ansatz jetzt \( \rho(u) \) gleich Null setzen und für \(u\) beliebige Geschwindigkeiten zulassen.
Bisher ist unser langsames Vortasten in Richtung eines relativistischen Gravitationsgesetzes zumindest konsistent. Bleibt die Frage: Was ist \( \rho(u) \) nun genau?
In der nichtrelativistischen Newtonschen Physik war \(\rho\) eine Massendichte. Ist zu erwarten, dass in der allgemeinen Relativitätstheorie ebenfalls nur Massen ein Gravitationsfeld erzeugen? Das wäre sehr merkwürdig, da schon in der speziellen Relativitätstheorie (träge) Masse in Energie umgewandelt werden kann. Angenommen, wir haben ein massives Teilchen vor uns, z.B. ein neutrales Pion. Dieses kann spontan in zwei masselose Photonen zerfallen. Wenn Gravitation nur von massiven Teilchen erzeugt würde, so würde diese Gravitation beim Zerfall des Teilchens in masselose Objekte plötzlich ausgeschaltet, was ziemlich unplausibel klingt. Plausibler wäre es, wenn auch bezüglich der Gravitationserzeugung Energie und Masse gleichwertig zueinander wären, so wie dies bezüglich der Trägheit bereits aufgrund der speziellen Relativitätstheorie der Fall ist. Die beiden Photonen, die beim Zerfall des Pions entstehen, sollten also genauso wie das Pion zuvor auch ein Gravitationsfeld erzeugen.
Massen- und Energiedichten werden in der speziellen Relativitätstheorie nicht durch eine skalare Funktion, sondern durch den sogenannten Energie-Impuls-Tensor dargestellt. Nur so kann man die relativistischen Zusammenhänge zwischen Massendichten, Energiedichten und Impulsen sowie deren Flüsse korrekt darstellen (wir gehen weiter unten noch genauer darauf ein).
Das passt gut zur obigen Gleichung \[ \mathrm{Ric}(u,u) = 4 \pi G_{N} \, \rho(u) \] denn auch aufgrund dieser Gleichung ist es naheliegend, für \( \rho(u) \) einen Tensoransatz zu machen: \[ \rho(u) c^{4} =: T(u,u) \] mit einem Tensor \(T\), der genau wie der Ricci-Tensor aus zwei Tangentialvektoren \(u\) und \(v\) eine reelle Zahl (nämlich \(T(u,v)\) ) macht.
Wir wollen annehmen, dass dieser symmetrische Tensor gerade der Energie-Impuls-Tensor ist (deshalb der Faktor \(c^{4}\), denn so erreichen wir, dass \(T_{00}\) die Dimension einer Energiedichte hat, wie wir gleich sehen werden).
In Komponenten schreiben wir wieder \[ T(u,v) = \sum_{\mu\nu} \, T_{\mu\nu} \, u^{\mu} v^{\nu} \] so dass wir für unseren Ansatz für das verallgemeinertes Gravitationsgesetz die Gleichung \[ R_{\mu\nu} = \frac{4 \pi G_{N}}{c^{4}} \, T_{\mu\nu} \] erhalten. Wir werden etwas weiter unten noch sehen, dass wir hier noch eine kleine Änderung einbauen müssen. Zunächst aber wollen wir uns den Energie-Impuls-Tensor genauer ansehen:
Die einfachste Form einer Materieverteilung, die Gravitation erzeugen kann, bezeichnen wir als Staub. Darunter stellen wir uns eine Wolke kleiner Staubkörnchen vor, die sich in einem bestimmten Bezugssystem alle in Ruhe befinden. Diese Aussage macht natürlich streng genommen nur lokal Sinn. Wir werden daher im folgenden immer nur kleine Raumbereiche separat betrachten, so dass wir in diesen Raumbereichen Riemannsche Normalkoordinaten einführen können und die metrische Matrix in diesen Koordinaten annähernd die Minkowski-Matrix ist. Wir setzen uns damit in das lokale momentane Ruhe-Inertialsystem eines kleinen Teils der Staubwolke.
Nun lassen wir in diesem Ruhesystem des Staubes zwei Testteilchen an eng benachbarten Stellen los und betrachten, wie ihre Bahnen aufgrund der Gravitation auseinanderdriften. Im Moment des Loslassens sollen die Teilchen in Ruhe sein, d.h. im Ruhesystem des Staubes gilt für die Vierergeschwindigkeiten \(u\) der beiden Teilchen \[ u = \begin{pmatrix} c \\ \boldsymbol{0} \end{pmatrix} \] Wenn wir von schwachen Gravitationsfeldern ausgehen, haben wir damit den nichtrelativistischen Grenzfall: Gravitationsquelle (Staub) und Testteilchen ruhen am Anfang relativ zueinander. Der Ausdruck \[ \rho(u) = \frac{1}{c^4} \, T(u,u) \] müsste also in die nichtrelativistische Massendichte \( \rho \) aus dem Newtonschen Gravitationsgesetz übergehen.
Setzen wir das obige Start-\(u\) in \(\rho(u)\) ein, so ergibt das \[ \rho\left( \begin{pmatrix} c \\ \boldsymbol{0} \end{pmatrix} \right) = \] \[ = \frac{1}{c^4} \, T\left(\begin{pmatrix} c \\ \boldsymbol{0} \end{pmatrix}, \begin{pmatrix} c \\ \boldsymbol{0} \end{pmatrix} \right) = \] \[ = \frac{1}{c^2} \, T_{00} \] d.h. es muss \[ T_{00} = \rho c^{2} \] sein.
Und das ist auch schon alles! Alle anderen Komponenten des Energie-Impuls-Tensors sind im Ruhesystem des Staubes Null! Letztlich wird der Begriff Staub genau durch diese Eigenschaft des Energie-Impuls-Tensors definiert.
Wie wir gleich sehen werden, bedeutet das, dass kein Druck sowie keine Kräfte zwischen den Staubteilchen vorliegen (Staub ist also nicht mit einem Gas zu verwechseln).
Nun können wir auch leicht die Massen-Energie-Dichte ausrechnen, die auf Testteilchen wirkt, die sich mit Vierergeschwindigkeit \[ u = \begin{pmatrix} \gamma c \\ \gamma \boldsymbol{v} \end{pmatrix} \] im lokalen Ruhesystem des Staubes bewegen: \[ \rho(u) = \frac{1}{c^4} \, T(u,u) = \] \[ = \frac{1}{c^4} \, T_{00} \, u^{0} u^{0} = \frac{1}{c^2} \rho \, u^{0} u^{0} = \] \[ = \rho \, \gamma^{2} \] Wir sehen hier sehr schön, dass die Massen/Energie-Dichte \(\rho\) keine skalare Funktion ist: Betrachtet man sie aus dem mit Vierergeschwindigkeit \(u\) bewegten Bezugssystem, so nimmt sie um den Faktor \(\gamma^{2}\) zu.
Ein Faktor \(\gamma\) repräsentiert dabei die Zunahme der kinetischen Energie der Staubteilchen, die ja aus dem mit \(u\) bewegten Bezugssystem heraus ebenfalls bewegt erscheinen.
Der andere Faktor \(\gamma\) repräsentiert die Lorentz-Kontraktion des Raumes: Der Raum erscheint in Bewegungsrichtung um den Faktor \(1/\gamma\) verkürzt, und die Staubteilchen drängen sich entsprechend auf weniger Raum zusammen, was die Energiedichte erhöht.
Zum Vergleich: eine ruhende elektrische Ladungsdichte \(\rho_{e}\) wird aus einem mit \(u\) bewegten Bezugssystem betrachtet nur um den Faktor \(\gamma\) zuzunehmen. Dort wirkt sich nur die Lorentzkontraktion aus; die Ladungen selber werden (anders als die Energie eines Teilchens) bei zunehmender Geschwindigkeit nicht größer. Daher ist die elektrische Ladungsdichte auch die Null-Komponente eines Vierervektors (die Vierer-Stromdichte), die Massen-Energie-Dichte dagegen die Null-Null-Komponente eines Tensors mit 2 Indizes (der Energie-Impuls-Tensor).
Natürlich kann man den Energie-Impuls-Tensor in jedes andere Bezugssystem umrechnen, denn das Transformationsverhalten ist ja durch die Tensoreigenschaft festgelegt: \(T(u,v)\) darf nicht vom Bezugssystem abhängen. Wir wollen hier noch nicht genauer darauf eingehen (Details folgen später).
Eine Eigenschaft des Energie-Impuls-Tensors ist noch wichtig: es gilt in der speziellen Relativitätstheorie für jeden Energie-Impuls-Tensor allgemein die Gleichung \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \] Dabei wurden die Indizes mit Hilfe der metrischen Matrix nach oben gezogen. Was diese Gleichung bedeutet, sehen wir weiter unten. Für den Energie-Impuls-Tensor von Staub können wir die Gleichung lokal im Ruhesystem des Staubes auswerten. Da nur \( T_{00} = T^{00} = \rho c^{2} \) ungleich Null ist, ergibt sich: \[ \frac{\partial}{\partial x^{0}} T^{00} = c \frac{d\rho}{dt} = 0 \] Im Ruhesystem der Staubkörnchen ändert sich also deren Massen-Energie-Dichte nicht. Das ist unmittelbar einleuchtend, denn wenn die Staubkörnchen sich nicht bewegen (ist ja das Ruhesystem), so ändert sich auch ihre räumliche Massenverteilung nicht.
Betrachten wir einen Energie-Impuls-Tensor \(T^{\mu\nu}\) (Indices mit der metrischen Matrix hochgezogen), der in einem lokalen frei fallenden Inertialsystem die folgende Gestalt hat: \(T^{\mu\nu}\) ist eine Diagonalmatrix mit \(T_{00} = \rho c^{2} \) (wie bei Staub) und \( T_{kk} = p \), also \[ (T^{\mu\nu}) = \begin{pmatrix} \rho c^{2} & 0 & 0 & 0 \\ 0 & p & 0 & 0 \\ 0 & 0 & p & 0 \\ 0 & 0 & 0 & p \end{pmatrix} \] Natürlich stellt sich die Frage: Welche Bedeutung hat \(p\) (der Buchstabe deutet es bereits an: \(p\) steht für den Druck)?
Dazu müssen wir uns einige generelle Gedanken über die Bedeutung der Komponenten \(T^{\mu\nu}\) in der speziellen Relativitätstheorie machen (also in karthesischen Minkowskikoordinaten). Siehe dazu z.B. Feynman Vorlesungen über Physik, Band II Elektromagnetismus und Struktur der Materie oder Landau, Lifschitz: Lehrbuch der theoretischen Physik, Band II: Klassische Feldtheorie, §32 Der Energie-Impuls-Tensor.
Wie oben bereits erwähnt, fordern wir für jeden Energie-Impuls-Tensor in der speziellen Relativitätstheorie in karthesischen Minkowskikoordinaten allgemein die Gleichung \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \] (warum, sehen wir später). Wir betrachten nun im vierdimensionalen Minkowskiraum alle Raum-Zeit-Punkte in einem bestimmten Zeitintervall und nennen die Menge dieser Raum-Zeit-Punkte \( V \). Anschaulich kann man sich einen vierdimensionalen Würfel in der Raumzeit vorstellen, bei dem man die drei Intervalle der räumlichen Koordinaten immer größer werden lässt und das zeitliche Intervall festhält. \(V\) ist also eine Zeitscheibe der Raumzeit mit einer bestimmten Zeitdicke.
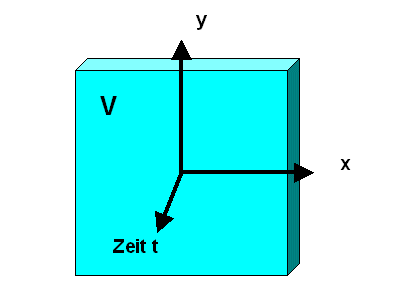
Bei der Größe
\[
\sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu}
\]
wollen wir deren Volumenintegral über
die Zeitscheibe \(V\) bilden:
\[
\int_{V} \, \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}}
T^{\mu\nu} \, dV =:
\]
\[ =
\int_{V} \, (\mathrm{div} \, T^{(\mu)} ) \, dV
\]
wobei \(T^{(\mu)}\) der Tangentialvektor mit Komponenten
\(T^{\mu\nu}\) ist.
In koordinatenunabhängiger Schreibweise wäre das
\[
(\mathrm{div} T^{(\mu)} ) \, dV =
d {\star}\omega^{T^{(\mu)}}
\]
ist mit der 1-Form
\[
\omega^{T^{(\mu)}} =
\sum_{\nu} \, T^{\mu}_{\;\nu} dx^{\nu}
\]
und dem Hodge-Sternoperator, der daraus eine 3-Form macht
(siehe die Definition der Divergenz in
Hodge-Sternoperator, Volumenform, Gradient, Divergenz, Rotation ).
Wir führen im Folgenden die koordinatenunabhängige Schreibweise immer mit auf, auch wenn wir sie
nicht unbedingt brauchen.
In Minkowskikoordinaten ist das Volumenelement \(dV\) einfach gegeben durch \( dx^{0} dx^{1} dx^{2} dx^{3} \) (das ist in der allgemeinen Relativitätstheorie in krummlinigen Koordinaten nicht so!). Der Integrand ist für jedes \(\mu\) also die folgende 4-Form (zu Differentialformen siehe Höhere Differentialformen und der Integralsatz von Stokes ): \[ \eta^{(\mu)} := \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} \, dx^{0} \wedge dx^{1} \wedge dx^{2} \wedge dx^{3} = \] \[ = (\mathrm{div} \, T^{(\mu)} ) \, dV = d {\star}\omega^{T^{(\mu)}} \] Diese 4-Form können wir andererseits als äußere Ableitung einer 3-Form schreiben: \[ \eta^{(\mu)} =: d\pi^{(\mu)} \] mit \[ \pi^{(\mu)} := \sum_{\nu} \, T^{\mu\nu} \, dA_{\nu} = {\star}\omega^{T^{(\mu)}} \] Dabei ist beispielsweise \[ dA_{0} = dx^{1} \wedge dx^{2} \wedge dx^{3} \] Nach dem Integralsatz von Stokes gilt nun \[ \int_{V} \, \eta^{(\mu)} = \int_{V} \, d\pi^{(\mu)} = \int_{\delta V} \, \pi^{(\mu)} = \, ... \] Das letzte Integral geht dabei über den Rand der Zeitscheibe \(V\). Wir wollen nun annehmen, dass zu jeder Zeit im Räumlich-Unendlichen der Energie-Impuls-Tensor hinreichend schnell gegen Null geht (was bei einer räumlich lokalisierten Materie-Energie-Verteilung selbstverständlich ist), so dass die Randintegrale über die räumlich unendlich fernen Randräume mit zwei Orts- und einer Zeitkoordinate gleich Null sind. Es bleiben dann nur die beiden Randraum-Integrale mit drei Ortskoordinaten und fester Zeitkoordinate übrig: \[ ... \, = \int_{\mathbb{R}^{3}} \, \pi^{(\mu)} \big|_{x_{0} = ct'} - \int_{\mathbb{R}^{3}} \, \pi^{(\mu)} \big|_{x_{0} = ct} \] Nun ist aber \( \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \), d.h. \(\eta^{(\mu)} = 0 \) und somit auch \[ \int_{V} \, \eta^{(\mu)} = \int_{\mathbb{R}^{3}} \, \pi^{(\mu)} \big|_{x_{0} = ct'} - \int_{\mathbb{R}^{3}} \, \pi^{(\mu)} \big|_{x_{0} = ct} = 0 \] Die beiden Integrale zur Zeit \(t\) bzw. \(t'\) müssen also gleich groß sein, und da \(t\) und \(t'\) beliebig sind, bedeutet das, dass das Integral \( \int_{\mathbb{R}^{3}} \, \pi^{(\mu)}\) nicht von der Zeit abhängt.
Da dieses Integral über einen Raum mit konstanter Zeit geht, trägt nur der Term mit \( dA_{0} = dx^{1} \wedge dx^{2} \wedge dx^{3} \) zum Integral bei: \[ \int_{\mathbb{R}^{3}} \, \pi^{(\mu)} = \int_{\mathbb{R}^{3}} \, T^{\mu0} \, dA_{0} = \] \[ = \int_{\mathbb{R}^{3}} \, T^{\mu0} \, dx^{1} dx^{2} dx^{3} =: \] \[ = \int_{\mathbb{R}^{3}} \, T^{\mu0} \, d^{3}x =: c \, P^{\mu} \] mit dem räumlichen Volumenelement \( d^{3}x = dx^{1} dx^{2} dx^{3} \) in karthesischen Koordinaten. Den Faktor \(c\) haben wir eingefügt, damit \(P^{\mu}\) die Dimension eines Impulses hat. Tatsächlich können wir \(P^{\mu}\) mit dem Gesamt-Viererimpuls der betrachteten Massen-Energie-Verteilung ansehen, wenn wir \(T^{00}\) als Energiedichte der Verteilung interpretieren, denn dann ist \[ c \, P^{0} = \int_{\mathbb{R}^{3}} \, T^{00} \, d^{3}x \] die Gesamtenergie der Verteilung, und da \(P^{\mu}\) wegen des Tensorcharakters von \(T^{\mu\nu}\) ein Vierervektor ist, muss \(P^{i}\) mit \(i\) = 1, 2, 3 der zugehörige räumliche Gesamtimpuls des Systems sein – nur so ist gesichert, dass z.B. eine ruhende Gesamtmasse nach einem Boost auch einen passenden Gesamt-Impuls besitzt. Halten wir fest:
|
Zusammenhang zwischen Gesamtimpuls-Vierervektor und Energie-Impulstensor: In der speziellen Relativitätstheorie gilt in den karthesischen Minkowski-Koordinaten eines jeden Inertialsystems: Einen Tensor \(T^{\mu\nu}\), der die Gleichung \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \] erfüllt und bei dem wir die Komponente \(T^{00}\) als Energiedichte der betrachteten Masse-Energieverteilung interpretieren, bezeichnen wir als Energie-Impuls-Tensor. Der Gesamt-Viererimpuls dieser Verteilung ist dann gegeben durch \[ P^{\mu} := \frac{1}{c} \, \int_{\mathbb{R}^{3}} \, T^{\mu0} \, d^{3}x \] Insbesondere ist \(P^{0}\) die Gesamtenergie der Verteilung. Dieser Gesamt-Viererimpuls ist wegen \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \] zeitlich konstant. Aufgrund der obigen Volumenintegration können wir den Vierervektor mit Komponenten \( T^{\mu0} / c \) als Vierer-Impulsdichte-Vektor der Verteilung interpretieren.
|
Aber wie kann man die anderen Komponenten von \( T^{\mu\nu} \)
mit \( \nu \gt 0 \) interpretieren?
Beginnen wir mit den räumlichen Komponenten \( T^{0j} \) mit \(j\) = 1, 2, 3 und schreiben die Gleichung \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \] für \(\mu = 0\) explizit aus: \[ \frac{1}{c} \frac{d}{d t} T^{00} + \sum_{j=1}^3 \, \frac{\partial}{\partial x^{j}} T^{0j} = 0 \] Wir können nun über ein räumliches Volumen \(G\) integrieren und im zweiten Integral den Integralsatz von Stokes für dreidimensionale Räume (auch Integralsatz von Gauß genannt) anwenden: \[ \frac{d}{d t} \, \int_{G} \, T^{00} \, d^{3}x = \] \[ = - c \, \int_{\delta G} \, \sum_{j} \, T^{0j} \, dA_{j} \] (die \(dA_{j}\) gehören hier zum zweidimensionalen räumlichen Flächenelement, d.h. sie sind die Komponenten des Flächenelement-Normalenvektors).
Links steht die zeitliche Veränderung der Energie bzw. Masse im Gebiet \(G\), und rechts steht demnach der Energiefluss durch die Oberfläche \( \delta G \) des Gebietes, denn die Gesamtenergie muss ja nach dem oben Gesagten erhalten bleiben. Daher können wir den räumlichen Vektor \[ \boldsymbol{S} := c \, \begin{pmatrix} T^{01} \\ T^{02} \\ T^{03} \end{pmatrix} \] als Energiestrom pro Flächeneinheit interpretieren, ganz analog zur Flächenstromdichte \( \boldsymbol{j} \) bei Ladungsströmen.
Nun fehlt nur noch die Interpretation der räumlichen Komponenten \( T^{ij} \) mit \(i\) = 1, 2, 3 und \(j\) = 1, 2, 3. Auch hier können wir wie gerade zuvor die Gleichung \[ \frac{1}{c} \frac{d}{d t} \, \int_{G} \, T^{i0} d^{3}x = \] \[ - \int_{\delta G} \, \sum_{j} \, T^{ij} \, dA_{j} \] herleiten. Da \( T^{\mu0} / c \) oben der Vierer-Impulsdichte-Vektor war, sind \( T^{i0} / c \) die räumlichen Komponenten des Impulsdichte-Vektors.
Auf der linken Seite steht also die zeitliche Änderung der i-ten räumlichen Komponente des Gesamtimpulses im Gebiet \(G\), und rechts steht demnach der Impulsfluss der i-ten Impulskomponente durch die Oberfläche von \(G\), denn der Gesamtimpuls muss insgesamt erhalten bleiben. Daher können wir den räumlichen Vektor \[ \boldsymbol{\sigma}^{(i)} := \begin{pmatrix} T^{i1} \\ T^{i2} \\ T^{i3} \end{pmatrix} \] als Impulsstrom der i-ten Impulskomponente pro Flächeneinheit interpretieren. Der Ausdruck \[ \sum_{j} \, T^{ij} \, dA_{j} = \boldsymbol{\sigma}^{(i)} \, \boldsymbol{dA} \] mit dem Skalarprodukt zwischen \( \boldsymbol{\sigma}^{(i)} \) und dem Flächenelement-Normalenvektor \( \boldsymbol{dA} \) ist also der durch das Flächenelement strömende Impulsfluss der i-ten Impulskomponente.
Nun kann man in vielen Fällen diesen Impulsstrom auch ganz anschaulich als eine Kraftwirkung auf das Flächenelement interpretieren. Man kann sich z.B. ein geschlossenes Gefäß vorstellen, in dem sich ein Gas befindet. Das Innere ist dann das Raumgebiet \(G\), und die dünne Gefäßwand ist der Rand \( \delta G \) des Raumgebietes. Schauen wir uns ein kleines Flächenelement auf der Gefäßwand mit Flächenelement-Normalenvektor \( \boldsymbol{dA} \) an. Die Gasmoleküle prallen auf die Gefäßwand, wodurch sich ihr Impuls ändert, d.h. es entsteht ein Impulsfluss durch die Wand. Dem entspricht eine Kraft auf die Wand, die genau der mittleren zeitlichen Änderung der Impulse der Gasmoleküle entspricht. Die Kraft pro Fläche ist gleich dem Impulsstrom pro Fläche. Daher können wir \[ \sum_{j} \, T^{ij} dA_{j} = \boldsymbol{\sigma}^{(i)} \, \boldsymbol{dA} \] auch interpretieren als i-te Komponente der Kraft, die auf das Flächenelement \(dA\) wirkt.
Man bezeichnet den 3-mal-3-Tensor \[ \sigma^{ij} = \boldsymbol{\sigma}^{(i),j} = T^{ij} \] auch als Spannungstensor. Mit ihm lassen sich die inneren Kräfte z.B. in Festkörpern oder Gasen beschreiben.
Wenn \( \sigma^{ij} \) diagonal ist mit identischen Diagonalelementen, so ist die Kraft immer parallel zum Flächenelement-Normalenvektor, also senkrecht zur Fläche. Das ist z.B. bei Gasen oder Flüssigkeiten der Fall, wenn man die Viskosität (Zähigkeit) vernachlässigt. Wenn wir in diesem Fall also \[ \sigma^{ij} =: p \, \delta^{ij} \] schreiben, so ist die Kraft \( \boldsymbol{F} \) auf ein Flächenelement mit Flächenelement-Normalenvektor \( \boldsymbol{dA} \) gegeben durch \( \boldsymbol{F} = p \, \boldsymbol{dA} \). Das ist für \(p\) genau die Definition des Drucks! Genau so hatten wir den Energie-Impulstensor für eine reibungsfreie Flüssigkeit (oder ein reibungsfreies Gas) oben aufgebaut, und nun wissen wir auch, warum \(p\) darin die Interpretation eines Drucks haben muss!
Es ist interessant, sich einmal die Analogien zwischen elektrischer Ladung und Energie bzw. Impuls klar zu machen – dann versteht man auch, warum man für Energie und Impuls einen Tensor braucht, für die elektrische Ladung dagegen nur einen Vierervektor:
|
Wir gehen zunächst einfach davon aus, dass wir für die relativistische Beschreibung elektrischer Ladungs- und Stromverteilungen einen Vierervektor \[ j = (j^{\mu}) = \begin{pmatrix} c\rho \\ \boldsymbol{j} \end{pmatrix} \] und für die relativistische Beschreibung von Energie- und Impulsverteilungen einen Tensor \[ T^{\mu\nu} \] benötigen. Es gelten die Kontinuitätsgleichungen \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \] \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} j^{\nu} = 0 \] Aufgrund dieser Kontinuitätsgleichungen kann man (wie weiter oben gezeigt) herleiten, dass die folgenden Größen zeitlich konstant sind: \[ c \, P^{\mu} := \int_{\mathbb{R}^{3}} \, T^{\mu0} \, d^{3}x \] \[ c \, Q := \int_{\mathbb{R}^{3}} \, j^{0} \, d^{3}x \] d.h. wir können \(j^{0}\) als die räumliche Dichte der Größe \( c \, Q \) und \(T^{\mu 0}\) für jedes \(\mu\) als die räumliche Dichte der Größe \( c \, P^{\mu} \) interpretieren. Jetzt sehen wir auch, warum wir für Energie und Impuls den Index \(\mu\) brauchen: nicht nur \(P^{0}\) ist erhalten, sondern auch \(P^{k}\). Und: Die Energie \(P^{0}\) ist anders als die Ladung \(Q\) kein Skalar, sondern die nullte Komponente eines Vierervektors, verhält sich also anders bei Bezugssystemwechseln (die Integrale rechts kann man auch invariant schreiben, indem man über einen raumartigen dreidimensionalen Schnitt durch die Raumzeit integriert). Gesamtenergie und Gesamtimpuls eines Systems müssen in der Relativitätstheorie einen zeitunabhängigen Vierervektor bilden (sofern keine äußeren Kräfte wirken)! Dies erklärt den ersten Index von \(T^{\mu\nu}\). Der zweite Index ist notwendig, wenn man zu den zeitunabhängigen Gesamt-Größen die entsprechenden zeitabhängigen räumlichen Dichten und Flächenstromdichten bilden möchte, so wie dies analog bei der elektrischen Stromdichte \(j^{\nu}\) der Fall ist. Dies zeigt der folgende Punkt:
Man kann aus der Kontinuitätsgleichung (wie weiter oben gezeigt)
die Gleichungen
\[
\frac{d}{d t} \, \int_{G} \,
T^{\mu0} \, d^{3}x =
\]
\[ = - c \,
\int_{\delta G} \,
\sum_{k} \,
T^{\mu k} \, dA_{k}
\]
So wie wir oben \(j^{0}\) als die räumliche Dichte der Größe \( c \, Q \) und \( T^{\mu 0} \) als die räumliche Dichte der Größe \( c \, P^{\mu} \) interpretieren, so können wir aufgrund dieser Gleichungen den räumlichen Vektor \( \boldsymbol{j} = (j^{k}) \) als Flächenstromdichte der Größe \( Q \) und den räumlichen Vektor \( \boldsymbol{T}^{(\mu)} := (T^{\mu k}) \) für jedes \( \mu \) als Flächenstromdichte der Größe \( P^{\mu} \) interpretieren.
|
Kommen wir noch einmal zurück zum Gesamt-Viererimpuls
\[
P^{\mu}
:= \frac{1}{c} \,
\int_{\mathbb{R}^{3}} \,
T^{\mu0} \, d^{3}x
\]
Diese Größe ist für eine Materie-Energie-Verteilung in einem gegebenen Inertialsystem
eindeutig und wegen
\[
\sum_{\nu} \, \frac{\partial}{\partial x^{\nu}}
T^{\mu\nu} = 0
\]
auch zeitunabhängig.
Es zeigt sich aber, dass verschiedene Energie-Impuls-Tensoren \( T^{\mu\nu} \) zum selben gesamt-Viererimpuls \( P^{\mu} \) führen können. Betrachten wir konkret den Tensor \[ (T ')^{\mu\nu} := T^{\mu\nu} + \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} \psi^{\mu\nu\sigma} \] mit Antisymmetrie in den beiden hinteren Indizes bei \(\psi\), also \[ \psi^{\mu\nu\sigma} = - \psi^{\mu\sigma\nu} \] Wir rechnen leicht nach, dass auch \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} (T ')^{\mu\nu} = 0 \] ist, denn wegen der Antisymmetrie von \(\psi^{\mu\sigma\nu}\) in den beiden hinteren Indices und der Vertauschbarkeit der Ableitungen ist \[ \sum_{\nu\sigma} \, \frac{\partial}{\partial x^{\nu}} \frac{\partial}{\partial x^{\sigma}} \psi^{\mu\nu\sigma} = 0 \] Außerdem ist der Gesamt-Viererimpuls von \(T^{\mu\nu}\) und \( (T ')^{\mu\nu} \) derselbe, wenn wir fordern, dass \(\psi^{\mu0\sigma}\) im räumlich Unendlichen (also dem unendlich fernen Rand \( \delta \mathbb{R}^{3} \)) so stark gegen Null geht, dass gilt (wegen der Antisymmetrie ist übrigens unten \( \psi^{\mu 0 0} = 0 \) ): \[ \int_{\mathbb{R}^{3}} \, \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} \psi^{\mu0\sigma} \, d^{3}x = \] \[ = \int_{\delta \mathbb{R}^{3}} \, \sum_{k = 1}^{3} \, \psi^{\mu 0 k} \, dA_{k} = 0 \] Woher kommt nun die Mehrdeutigkeit im Energie-Impuls-Tensor? Im Grunde reicht die Formel \[ P^{\mu} := \frac{1}{c} \, \int_{\mathbb{R}^{3}} \, T^{\mu0} \, d^{3}x \] nicht aus, um \( T^{\mu0} \, d^{3}x \) als Vierer-Impulskomponenten des Volumenelementes zu interpretieren.
Man weiß lediglich, dass die Terme über das gesamte Volumen aufintegriert den Gesamt-Viererimpuls ergeben. Wir können jedoch ein weiteres Objekt hinzunehmen; den vierdimensionalen Drehimpulstensor. Eine detaillierte Darstellung dazu findet man z.B. in Landau, Lifschitz: Lehrbuch der theoretischen Physik, Band II: Klassische Feldtheorie. Dort wird gezeigt, dass im vierdimensionalen Drehimpulstensor sich die Terme \( T^{\mu0} \, d^{3}x \) nur dann als Vierer-Impulskomponenten des Volumenelementes interpretieren lassen, wenn der Energie-Impuls-Tensor \(T^{\mu\nu}\) symmetrisch ist! Schauen wir uns das etwas genauer an:
In der speziellen Relativitätstheorie ist die Zeitunabhängigkeit des Gesamt-Viererimpulses \(P^{\mu}\) eine Folge davon, dass Verschiebungen der Raum- und Zeitkoordinate die Physik des Systems nicht ändern (Translationsinvarianz). Insgesamt muss aber die Physik in der speziellen Relativitätstheorie unter einer größeren Symmetriegruppe invariant sein: der Poincarégruppe. Neben Translationen der Raum-Zeit-Koordinaten gehören dazu die Lorentztransformationen, also die linearen Transformationen der Raum-Zeit-Koordinaten, so dass sich die Minkowskimetrik von Vierervektoren nicht ändert (siehe Kapitel 3.5 Die mathematische Struktur der Poincarégruppe ). Die Invarianz unter Lorentztransformationen führt zu einer weiteren zeitlich erhaltenen Größe: dem vierdimensionalen antisymmetrischen Drehimpulstensor. Bei einem System aus Massepunkten (Teilchen) lautet dieser Tensor: \[ M^{\mu\nu} := \sum_{n} \, ( x^{\mu}_{n} \, p^{\nu}_{n} - x^{\nu}_{n} \, p^{\mu}_{n} ) \] Dabei kennzeichnet der Index \(n\) das \(n\)-te Teilchen. Bei den räumlichen Komponenten erkennt man den dreidimensionalen Drehimpulsvektor \(\boldsymbol{L}\) wieder: \[ L^{3} = M^{12} \] usw.. Wenn wir nun zu einer kontinuierlichen Massenverteilung übergehen, so würden wir gemäß der Formel \[ P^{\mu} := \frac{1}{c} \, \int_{\mathbb{R}^{3}} \, T^{\mu0} \, d^{3}x \] gerne den Term \[ \frac{1}{c} \, T^{\mu0} \, d^{3}x \] als \(\mu\)-te Impulskomponente des Volumenelementes \( d^{3}x \) interpretieren. Wenn wir das tun und diesen Term für die Impulskomponenten \(p^\mu_n\) in der \(M^{\mu\nu}\)-Formel einsetzen sowie die Summe durch ein Raumintegral ersetzen, dann hätte \( M^{\mu\nu} \) die Form \[ M^{\mu\nu} = \frac{1}{c} \, \int_{\mathbb{R}^{3}} \, ( x^{\mu} T^{\nu0} - x^{\nu} T^{\mu0} ) \, d^{3}x \] Welche Bedingung muss der Integrand erfüllen, damit dieser Tensor zeitunabhängig ist? Vergleichen wir diesen Ausdruck mit dem zeitunabhängigen Viererimpuls \[ P^{\mu} := \frac{1}{c} \, \int_{\mathbb{R}^{3}} \, T^{\mu0} \, d^{3}x \] Wenn wir darin \( T^{\mu 0} \) durch \( ( x^{\mu} T^{\nu0} - x^{\nu} T^{\mu0} ) \) ersetzen, so erhalten wir den Drehimpulstensor \(M^{\mu\nu}\). Nun hatten wir oben gezeigt, dass die Kontinuitätsgleichung \[ \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} T^{\mu\sigma} = 0 \] zur Zeitunabhängigkeit von \(P^{\mu}\) führt. Analog fordern wir die Kontinuitätsgleichung \[ \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} ( x^{\mu} T^{\nu\sigma} - x^{\nu} T^{\mu\sigma} ) = 0 \] und können vollkommen analog zum Viererimpuls die Zeitunabhängigkeit nachrechnen. Diese Gleichung können wir weiter vereinfachen, wobei wir \( \frac{\partial}{\partial x^{\sigma}} x^{\mu} = \delta^{\mu}_{\sigma} \) sowie die Kontinuitätsgleichung \( \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} \, T^{\mu\sigma} = 0 \) verwenden: \[ \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} ( x^{\mu} T^{\nu\sigma} - x^{\nu} T^{\mu\sigma} ) = \] \[ = T^{\nu\mu} - T^{\mu\nu} = 0 \] d.h. der Energie-Impuls-Tensor muss symmetrisch sein. Halten wir fest:
|
Symmetrie des Energie-Impuls-Tensors: Wenn wir für den Gesamtimpuls und den vierdimensionalen Drehimpulstensor gleichzeitig die Ausdrücke \[ P^{\mu} := \frac{1}{c} \, \int_{\mathbb{R}^{3}} \, T^{\mu0} \, d^{3}x \] \[ M^{\mu\nu} = \frac{1}{c} \, \int_{\mathbb{R}^{3}} \, ( x^{\mu} T^{\nu0} - x^{\nu} T^{\mu0} ) \, d^{3}x \] verwenden wollen, so dass der Term \[ \frac{1}{c} \, T^{\mu0} \, d^{3}x \] als \(\mu\)-te Impulskomponente des Volumenelementes \(d^{3}x\) interpretiert werden kann, und wenn Gesamtimpuls und Drehimpulstensor zeitlich konstant sein sollen (also eine entsprechende Kontinuitätsgleichung erfüllen), so muss der Energie-Impuls-Tensor \( T^{\mu\nu} \) symmetrisch sein. |
Ein letztes Argument für die Symmetrie zumindest der räumlichen Komponenten
von \(T^{\mu\nu}\) ergibt sich, wenn man das Drehmoment, das auf ein Volumen wirkt,
einmal über die im Volumen wirkende Kraftdichte und einmal über die Kraft auf die
Oberfläche ausdrückt. Nur wenn die räumlichen Komponenten von \(T^{\mu\nu}\)
symmetrisch sind, stimmen die beiden Ausdrücke überein, so dass die Integranden
auch die beabsichtigte Interpretation haben können.
Man kann sich überlegen, dass man oben in \[ (T ')^{\mu\nu} := T^{\mu\nu} + \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} \psi^{\mu\nu\sigma} \] den freien Zusatzterm \( \psi^{\mu\nu\sigma} \) immer so wählen kann, dass der Energie-Impuls-Tensor symmetrisch wird, so dass wir den Vierervektor mit Komponenten \( T^{\mu0} \) wirklich als Vierer-Impulsdichte-Vektor der Verteilung interpretieren können. Auch die anderen Komponenten von \( T^{\mu\nu} \) haben dann erst die oben beschriebene Interpretation.
Schauen wir uns an, wie man ein passendes \( \psi^{\mu\nu\sigma} \) findet: Zunächst einmal kann man ein allgemeines (nicht unbedingt symmetrisches) \(T^{\mu\nu}\) aufteilen in einen symmetrischen und einen antisymmetrischen Anteil: \[ T^{\mu\nu} = \frac{1}{2} \, (T^{\mu\nu} + T^{\nu\mu}) + \frac{1}{2} \, (T^{\mu\nu} - T^{\nu\mu}) \] Wenn man nun den Term \[ \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} \psi^{\mu\nu\sigma} \] mit \( \psi^{\mu\nu\sigma} = - \psi^{\mu\sigma\nu} \) zu \(T^{\mu\nu}\) hinzuaddiert, so soll dieser den antisymmetrischen Anteil neutralisieren: \[ \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} \psi^{\mu\nu\sigma} = - \frac{1}{2} \, (T^{\mu\nu} - T^{\nu\mu}) \] Eine Lösung dieser Gleichung ist \[ \psi^{\mu\nu\sigma} = \frac{1}{2} \, ( x^{\mu} T^{\nu\sigma} - x^{\nu} T^{\mu\sigma} ) \] denn wir hatten oben beim Drehimpulstensor bereits die Gleichung \[ \sum_{\sigma} \, \frac{\partial}{\partial x^{\sigma}} ( x^{\mu} T^{\nu\sigma} - x^{\nu} T^{\mu\sigma} ) = \] \[ = T^{\nu\mu} - T^{\mu\nu} \] gezeigt.
Es ergibt sich eine sehr interessante Konsequenz, wenn wir die beiden räumlichen Vektoren mit Komponenten \( T^{i0} \) bzw. \( T^{0i} \) miteinander vergleichen (siehe oben):
| Aus der Symmetrie von \(T^{\mu\nu}\) folgt, dass ein Energiestrom immer mit einem Impuls verbunden ist! Der Energie-Stromflächendichte-Vektor ist gleich dem Impulsdichtevektor (mal \(c^{2}\)). |
Energie verhält sich also in diesem Sinne genau wie Masse (die hier auch als
Energie gerechnet wird). Man kann sich anhand von Beispielen leicht von der Richtigkeit
dieser Aussage überzeugen. Schauen wir uns beispielsweise in einem
gegebenem Inertialsystem einen Fluss von Teilchen der Masse \(m\) an, die sich alle
mit der Geschwindigkeit \(\boldsymbol{v}\) bewegen. Die Anzahldichte im Bezugssystem
(Teilchenzahl pro Volumeneinheit) bezeichnen wir mit \(n\), und Energie und Impuls eines
Teilchens bezeichnen wir mit \(E\) und \(\boldsymbol{p}\).
Dann sind die Energie-Flächenstromdichte \( \boldsymbol{j} \)
(Energiedurchfluss pro Zeiteinheit und Flächeneinheit)
und die Impulsraumdichte \(\boldsymbol{j'}\) (Impuls pro Volumeneinheit)
gegeben durch
\[
\boldsymbol{j} = n E \boldsymbol{v}
\]
\[
\boldsymbol{j'} = n \boldsymbol{p}
\]
Für Teilchen mit Masse \(m\) ist \( E = m c^{2} \gamma \)
(dabei ist \(\gamma\) der Lorentzfaktor) und
deshalb
\[
\boldsymbol{p} = m \gamma \boldsymbol{v} = E \boldsymbol{v} / c^{2}
\]
Auch für masselose Teilchen gilt \( \boldsymbol{p} = E \boldsymbol{v} / c^{2} \)
mit \( |\boldsymbol{v}| = c \).
Daher ist in beiden Fällen \( E \boldsymbol{v} = \boldsymbol{p} c^2 \)
und somit
\[
\boldsymbol{j} = n E \boldsymbol{v} = n \boldsymbol{p} c^{2}
= \boldsymbol{j'} c^{2}
\]
Einstein hat noch ein anderes schönes Argument für diesen Zusammenhang gegeben, das mit dem
Schwerpunkt eines geschlossenen Wagens zu tun hat, in dem eine Energie von einer Wand zur anderen Wand strömt.
Wer möchte, kann diesen Gedankengang beispielsweise nachlesen in
Feynman Vorlesungen über Physik, Band II Elektromagnetismus und Struktur der Materie.
Für den Energie-Impuls-Tensor einer reibungsfreien Flüssigkeit bzw. eines reibungsfreien Gases hatten wir oben bereits den Ansatz gemacht, dass im lokalen Ruhesystem der Flüssigkeit \(T^{\mu\nu}\) eine Diagonalmatrix ist mit \( T_{00} = \rho c^{2} \) (wie bei Staub) und \( T_{kk} = p \) (die Indexstellung ist hier egal). Die obige Diskussion hat gezeigt, dass wir \( \rho \) als Massendichte bzw. \( \rho c^{2} \) als Energiedichte der Flüssigkeit und \(p\) als den Druck interpretieren können, denn \( T^{ij} =: p \, \delta^{ij} \) ist diagonal mit identischen Diagonalelementen, so dass die Druckkraft immer senkrecht zur Fläche wirkt (es gibt also keine Viskosität (Zähigkeit) ). Die Kraft \( \boldsymbol{F} \) auf ein Flächenelement mit Flächenelement-Normalenvektor \( \boldsymbol{dA} \) ist dann gegeben durch \( \boldsymbol{F} = p \, \boldsymbol{dA} \), so wie das bei einem Druck der Fall sein muss.
Rechnen wir wieder die Massen-Energie-Dichte aus, die ein Testteilchen sieht, welches sich mit Vierergeschwindigkeit \( u = (\gamma c, \gamma \boldsymbol{v}) \) im lokalen Ruhesystem der Flüssigkeit oder des Gases bewegen: \[ \rho(u) = \frac{1}{c^4} \, T(u,u) = \] \[ = \frac{1}{c^4} \, T_{00} \, u^{0} u^{0} + \frac{1}{c^4} \, \sum_{k} \, T_{kk} \, u^{k} u^{k} = \] \[ = \rho \gamma^{2} + \frac{1}{c^4} \, p \gamma^{2} v^{2} = \] \[ = \rho \gamma^{2} + \frac{1}{c^2} \, p \, (\gamma^{2} - 1) \] denn beim Übergang zur letzten Zeile ist \[ \gamma^{2} \, (v/c)^{2} = \] \[ = \frac{(v/c)^2}{1 - (v/c)^2} = \] \[ = \frac{1 - (1 - ((v/c)^2)}{1 - (v/c)^2} = \] \[ = \frac{1}{1 - (v/c)^2} - 1 = \] \[ = \gamma^2 - 1 \] Wir haben also \[ \rho(u) = \frac{1}{c^4} \, T(u,u) = \] \[ = \rho \gamma^{2} + \frac{1}{c^2} \, p \, (\gamma^{2} - 1) \] Das bewegte Testteilchen nimmt also nicht nur (wie bei Staub) eine um \( \gamma^{2} \) verstärkte Energie-Massendichte \( \rho \) wahr, sondern auch der Druck \(p\) trägt zur wahrgenommenen Energiedichte bei.
Das kann man auch anschaulich verstehen: Zwar ruht die Flüssigkeit (das Gas) lokal in unserem Bezugssystem, d.h. die Komponenten \( T^{i0} \) und damit die Gesamtimpulse \( P^{i} \) sind Null. Dennoch aber bewegen sich natürlich die Moleküle statistisch und bauen so den Druck auf. Diese mikroskopischen Geschwindigkeiten verändern sich beim Bezugssystemwechsel und sorgen so für einen Energiedichte-Beitrag, der berücksichtigt werden muss.
Man kann über Lorentztransformationen nun den Energie-Impuls-Tensor in jedes andere Bezugssystem umrechnen, also z.B. den Energie-Impuls-Tensor einer sich gleichförmig bewegenden reibungsfreien Flüssigkeit (Gas) ausrechnen. Die Form des Energie-Impuls-Tensors im Ruhesystem der Flüssigkeit bestimmt zusammen mit dem Transformationsgesetz eindeutig den Energie-Impuls-Tensor in einem anderen Inertialsystem, denn man kann diesen ja über das Transformationsgesetz eindeutig ausrechnen. Wenn wir daher eine allgemeine Formel für den Energie-Impuls-Tensor angeben, die im lokalen Ruhesystem den korrekten Ruhe-Energie-Impuls-Tensor ergibt und die sich relativistisch richtig transformiert, so ist diese Formel eindeutig. Für den Energie-Impuls-Tensor einer reibungsfreien Flüssigkeit lautet diese allgemeine Formel:
|
Allgemeine Form des Energie-Impuls-Tensors einer reibungsfreien Flüssigkeit (Gas)
in einem beliebigen lokalen Inertialsystem: \[ T^{\mu\nu} = \left( \rho + \frac{1}{c^2} p \right) \, v^{\mu} v^{\nu} - p \, g^{\mu\nu} \] mit dem Vierer-Geschwindigkeitsvektor \( v = (v^{\mu}) \) der Flüssigkeit (Gas). Im Ruhesystem der Flüssigkeit (des Gases) ist \( v = (c, \boldsymbol{0}) \) und wir haben \[ T^{\mu\nu} = \left( \rho + \frac{1}{c^2} p \right) \, c^{2} \, \delta^{\mu 0} \delta^{\nu 0} - p \, g^{\mu\nu} \] d.h. \( T^{00} = \rho c^{2} \) und \( T^{kk} = p \) wie gefordert. Wir können daher \(v\) als die lokale Vierergeschwindigkeit der reibungsfreien Flüssigkeit (des Gases) interpretieren. |
Es gibt natürlich neben druckfreiem Staub und reibungsfreien Flüssigkeiten (Gasen) noch weitere
Materieformen, die i.a. auch andere Energie-Impuls-Tensoren aufweisen.
Ein Beispiel sind Festkörper oder auch viskose Flüssigkeiten, die auch
interene Kräfte parallel zu Schnittflächen aufweisen können (sogenannte Scherkräfte).
Zumeist sind diese Scherkräfte allerdings deutlich kleiner als Druck- oder Zugkräfte, so dass
man sie vernachlässigt.
Ein anderes Beispiel ist das elektromagnetische Feld, das ebenfalls einen Energie-Impuls-Tensor besitzt. Die konkrete Formel findet man in jedem Buch über Elektrodynamik oder auch im Internet (siehe z.B. Wikipedia: Energie-Impuls-Tensor). Wichtig ist, dass hier die Spur des Tensors Null ist: \[ \mathrm{Spur}_{g} T = \sum_{\mu\nu} \, g_{\mu\nu} \, T^{\mu\nu} = 0 \] Es ist interessant, dass innere Kräfte überhaupt einen Beitrag zur Energiedichte leisten, wenn man sie aus einem anderen Bezugssystem heraus betrachtet. Und dennoch müssen sie berücksichtigt werden, wenn man Energiedichten relativistisch korrekt beschreiben möchte. Ein schönes Beispiel dazu findet man in Feynman Vorlesungen über Physik, Band II Elektromagnetismus und Struktur der Materie, Kapitel 28 Elektromagnetische Masse. Dort wird eine kugelförmige statische negative Ladungsverteilung (also eine Ladungskugel) betrachtet, mit der man versuchsweise z.B. ein Elektron modellieren kann. Diese Ladungsverteilung erzeugt ein elektrisches Feld, das eine gewisse Energie aufweist. Beschleunigt man nun das Elektron und betrachtet Energie und Impuls, so stellt man fest, dass diese Größen sich nicht wie erwartet verhalten. Die Ursache dafür kennen wir nun: In einer kugelförmigen statischen negativen Ladungsverteilung stoßen sich die einzelnen Teile gegenseitig ab. Es muss daher Kräfte geben, die diese Abstoßung kompensieren und die Kugel zusammenhalten. Diese Kräfte muss man berücksichtigen, um das Verhalten für Energie und Impuls der Gesamtverteilung korrekt zu beschreiben.
In den meisten Fällen ist der Energie-Impuls-Tensor reibungsfreier Flüssigkeiten (also meist Gasen oder Plasma oder auch Staub, wenn man den Druck gleich Null setzt) für die Beschreibung von gravitationserzeugender Materie vollkommen ausreichend. Verschiedene Materieformen unterscheiden sich dabei durch eine jeweils charakteristische Zustandsgleichung der Materie, die im lokalen Ruhesystem den Druck \(p\) und die Energiedichte \(\rho\) miteinander verknüpft: \[ p = f(\rho) \] mit einer Materie- und Temperatur-abhängigen Funktion \(f\). Hier sind einige charakteristische Zustandsgleichungen:
|
Zustandsgleichungen: Die meisten reibungsfreien Flüssigkeiten (z.B. Gas): \[ p = k \rho \] mit einer Materie- und Temperatur-abhängigen Konstante \(k\). Staub (nichtrelativistische kollisionsfreie Materie, niedrige Temperatur): \[ p = 0 \] d.h. \( k = 0 \). Strahlung (inkohärentes Photonengas oder hochrelativistisches Gas mit sehr hoher Temperatur): \[ p = \frac{1}{3} \, \rho c^{2} \] d.h. \( k = \frac{1}{3} c^2 \). Es folgt, dass die Spur wie beim Energie-Impuls-Tensor des elektromagnetischen Feldes gleich Null ist (so muss es für elektromagnetische Strahlung ja auch sein): \[ \mathrm{Spur}_{g} T = \sum_{\mu\nu} \, g_{\mu\nu} T^{\mu\nu} = 0 \] |
Wir übertragen die obigen Energie-Impuls-Tensoren wie üblich in die gekrümmte Raumzeit, indem wir lokal in einem beliebigen Punkt \(p\) Riemannsche Normalkoordinaten einführen (also lokal ein frei fallendes Bezugssystem wählen) und dann fordern, dass bei ruhender Materie in diesem Punkt der Energie-Impuls-Tensor die obige Ruhesystem-Form annimmt.
Da wir das an jedem Punkt so machen können, sind zunächst keine Probleme zu erwarten. Auch für beliebige Bezugssysteme können wir den Energie-Impuls-Tensor angeben, denn die Formel \[ T^{\mu\nu} = \left( \rho + \frac{1}{c^2} p \right) \, v^{\mu} v^{\nu} - p \, g^{\mu\nu} \] ist tensoriell und macht daher auch in beliebigen Bezugssystemen Sinn. Interessanter wird es dann, wenn wir die Kontinuitätsgleichung \[ \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} T^{\mu\nu} = 0 \] und die damit zusammenhängende Interpretation des Energie-Impuls-Tensors in die gekrümmte Raumzeit übertragen wollen.
Als Verallgemeinerung der Kontinuitätsgleichung bietet sich die folgende tensorielle Gleichung an: \[ \sum_{\nu} \, D_{\nu} T^{\mu\nu} = 0 \] mit den kovarianten Ableitungen \[ D_{\nu} = D_{\frac{\partial}{\partial x^{\nu}}} \] Auf diese Weise ist gesichert, dass sich im Grenzfall verschwindender Gravitation in karthesischen Minkowskikoordinaten wieder die obige Kontinuitätsgleichung aus der speziellen Relativitätstheorie ergibt.
Man kann diese Kontinuitätsgleichung auch in die folgende Form bringen (siehe [MV] Kap. 4.6 ): \[ \frac{1}{|\det{g}|} \, \sum_{\nu} \, \frac{\partial}{\partial x^{\nu}} ( |\det{g}| \, T^{\mu\nu} ) = \] \[ = - \sum_{\nu\sigma} \, \Gamma^{\mu}_{\nu\sigma} T^{\nu\sigma} \] mit der Determinante \( \det{g} \) der metrischen Matrix. Die genaue Interpretation der Kontinuitätsgleichung im Sinne der Energie-Impuls-Erhaltung ist offenbar nicht ganz unproblematisch, wie diese komplizierte Gleichung vermuten lässt. Darin spiegelt sich wider, dass Materie und Gravitationsfeld Energie und Impuls austauschen können. Allgemein ist es keineswegs trivial, für ein System mit Gravitation überhaupt den Gesamt-Energie und -Impuls sauber zu definieren. Es gibt hierzu verschiedene Ansätze, die jeweils ihre Vor- und Nachteile haben.
Wenn wir uns das bisher Erreichte ansehen, so könnte man davon ausgehen, dass wir soweit bereits fertig sind: Wir haben oben als Ansatz für das verallgemeinertes Gravitationsgesetz die Gleichung \[ R_{\mu\nu} = \frac{4 \pi G_{N}}{c^{4}} \, T_{\mu\nu} \] gefunden, wir kennen den Ricci-Tensor auf der linken Seite und wir wissen, wie der Energie-Impuls-Tensor auf der rechten Seite aussieht und wie er (zumindest lokal bzw. im Grenzwert verschwindender Gravitation) interpretiert werden kann. Tatsächlich war auch Albert Einstein zu einem bestimmten Zeitpunkt dieser Meinung, bis sich herausstellte, dass er ein unscheinbares Detail übersehen hatte: Die Kontinuitätsgleichung!
Kehren wir noch einmal zurück zu unserer Gezeitenkräfte-Argumentation, die zu der obigen Gleichung geführt hatte: An einer Stelle hatten wir in Analogie zur nichtrelativistischen Gleichung \[ \mathrm{Spur} (K) = \] \[ = \mathrm{div} \, (\mathrm{grad} \, \phi) = 4 \pi G_{N} \, \rho \] die relativistische Gleichung \[ \mathrm{Ric}(u,u) = 4 \pi G_{N} \, \rho(u) \] aufgestellt, und für die Massen-Energiedichte \( \rho(u) \), die die benachbarten Testteilchen sehen, den einfachen tensoriellen Ansatz \[ \rho(u) \, c^{4} = T(u,u) \] mit dem Energie-Impuls-Tensor \( T(u,u) \) gemacht.
Das ist sicher zunächst die einfachste Möglichkeit. Im nichtrelativistischen Grenzfall ist die innere Teilchenbewegung der Materie klein und der Druck kann vernachlässigt werden, d.h. die Materie verhält sich wie Staub und wir haben \( \rho(u) = \rho \gamma^{2} \) (siehe weiter oben). Für kleine Geschwindigkeiten der Testteilchen ist dann \(\gamma\) ungefähr gleich 1 und es ergibt sich wie gewünscht \( \rho(u) = \rho \).
Aber: der naheliegende Ansatz \( \rho(u) \, c^{4} = T(u,u) \) ist nicht die einzige Möglichkeit, die den richtigen nichtrelativistischen Grenzwert ergibt. Hier ist ein anderer Kandidat: \[ \rho(u) \, c^{4} = \] \[ = \xi \, T(u,u) + (1 - \xi) \, T \, g(u,u) \] mit einer beliebigen reellen Zahl \(\xi\) sowie \[ T := \mathrm{Spur}_{g} T = \sum_{\mu\nu} \, g_{\mu\nu} \, T^{\mu\nu} \] (analog zum Ricci-Skalar) und \[ g(u,u) = c^{2} \] Für verschwindenden Druck und kleine Geschwindigkeiten ist sowohl \( T(u,u) = \rho c^{4} \) als auch \( T \, g(u,u) = \rho c^{4} \), so dass sich für beliebiges reelles \(\xi\) der richtige Grenzwert \( \rho(u) = \rho \) ergibt.
Aber welchen Wert für \(\xi\) sollen wir nun wählen? Für \(\xi=1\) würden wir unseren alten Ansatz zurückerhalten, aber diese Wahl scheint keineswegs zwingend zu sein. Der nichtrelativistische Grenzwert kann diese Frage nicht beantworten. Aber: die Kontinuitätsgleichung für den Energie-Impuls-Tensor kann es (da muss man natürlich erst einmal drauf kommen)!
Die Gleichung \[ \mathrm{Ric}(u,u) = 4 \pi G_{N} \, \rho(u) \] bedeutet in Komponenten ausgeschrieben mit unserem erweiterten Ansatz für \(\rho(u)\): \[ R_{\mu\nu} = \frac{4 \pi G_{N}}{c^{4}} \, ( \xi \, T_{\mu\nu} + (1 - \xi) \, T \, g_{\mu\nu} ) \] In Raumbereichen ohne Materie und Energie (also \( T_{\mu\nu} = 0 \) und deshalb auch \( T = 0 \)) ist demnach weiterhin \( R_{\mu\nu} = 0 \), so wie wir das auch weiter oben geraten hatten. Das ist schon mal gut so.
Bilden wir von dieser Gleichung mit Hilfe der Metrik die Spur (also \( \sum_{\mu\nu} \, g^{\mu\nu} \, ... \) ), sodass wir links den Ricci-Skalar \(R\) bekommen, so ergibt sich wegen \[ \sum_{\mu\nu} \, g^{\mu\nu} g_{\mu\nu} = \sum_{\mu} \delta^{\mu}_{\;\mu} = 4 \] die Gleichung \[ R = \frac{4 \pi G_{N}}{c^{4}} \, ( \xi \, T + 4 \, (1 - \xi) \, T) = \] \[ = \frac{4 \pi G_{N}}{c^{4}} \, (4 - 3 \xi) \, T \] Wir wollen hier nicht im Detail \( \xi \) ausrechnen, sondern einfach die Lösung angeben und diese dann rechtfertigen: der richtige Wert lautet \[ \xi = 2 \] Und hier kommt die Begründung: Mit \( \xi = 2 \) ergibt die obige Gleichung \[ R = \frac{4 \pi G_{N}}{c^{4}} \, (4 - 3 \xi) \, T = \] \[ = \frac{4 \pi G_{N}}{c^{4}} \, (-2) \, T = \] \[ = - \frac{8 \pi G_{N}}{c^{4}} \, T \] und die Gleichung \[ R_{\mu\nu} = \frac{4 \pi G_{N}}{c^{4}} \, ( \xi \, T_{\mu\nu} + (1 - \xi) \, T \, g_{\mu\nu} ) \] vereinfacht sich zu \[ R_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, ( T_{\mu\nu} - \frac{1}{2} \, T \, g_{\mu\nu} ) \] In diese Gleichung können wir \( R = - \frac{8 \pi G_{N}}{c^{4}} \, T \) einsetzen und erhalten \[ R_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, T_{\mu\nu} + \frac{1}{2} \, R \, g_{\mu\nu} \] oder umgestellt \[ R_{\mu\nu} - \frac{1}{2} \, R \, g_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, T_{\mu\nu} \] Den Tensor auf der linken Seite bezeichnet man auch als Einstein-Tensor: \[ G_{\mu\nu} := R_{\mu\nu} - \frac{1}{2} \, R \, g_{\mu\nu} \] d.h. unser Ansatz für das verallgemeinerte Gravitationsgesetz lautet nun \[ G_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, T_{\mu\nu} \] Die Begründung für \( \xi = 2 \) (das haben wir ja bereits verwendet) ergibt sich nun, wenn wir die vierdimensionale Divergenz bilden. Es gilt nämlich bei verschwindender Torsion und einer Metrik, die mit der kovarianten Ableitung verträglich ist, die sogenannte kontrahierte Bianchi-Identität (siehe z.B. [MV2] Kap. 6,7 ; man kann diese Identität aus der zweiten Bianchi-Identität (siehe Krümmung ) durch geeignete Spurbildung mit Hilfe der Metrik nachrechnen – wir überspringen dies hier): \[ \sum_{\nu} \, D_{\nu} G^{\mu\nu} = 0 \] Aus dem verallgemeinerten Gravitationsgesetz folgt damit automatisch die Gleichung \[ \sum_{\nu} \,D_{\nu} T^{\mu\nu} = 0 \] wie es für den Energie-Impuls-Tensor sein muss. Dieses Ergebnis erhalten wir nur für \( \xi = 2\). Wir sehen, mit welchen trickreichen Detail Einstein zu kämpfen hatte!
Es zeigt sich, dass das obige Gravitationsgesetz keine weiteren versteckten Fallstricke enthält. Außerdem hat es seit seiner Formulierung durch Einstein im Jahr 1915 alle experimentellen Tests ohne Probleme überstanden und gilt daher als das allgemein akzeptierte Gesetz zur relativistischen Beschreibung der Gravitation. Fassen wir dies noch einmal zusammen:
|
Das relativistische Gravitationsgesetz (die Einsteinschen Feldgleichungen): Der Energie-Impuls-Tensor \( T_{\mu\nu} \) der Materie und die Krümmung der vierdimensionalen Raumzeit sind über die sogenannten Einsteinschen Feldgleichungen miteinander verknüpft. Diese lauten: \[ G_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, T_{\mu\nu} \] Dabei verwenden wir:
Eine dazu gleichwertige Form ist \[ R_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, ( T_{\mu\nu} - \frac{1}{2} \, T \, g_{\mu\nu} ) \] mit \[ T := \sum_{\nu\sigma} \, g^{\nu\sigma} T_{\nu\sigma} \] denn es gilt \[ R = - \frac{8 \pi G_{N}}{c^{4}} \, T \] In Raumbereichen ohne Materie und Energie (also \( T_{\mu\nu} = 0 \)) ist demnach \( R_{\mu\nu} = 0 \), aber \( R^{\mu}_{\;\nu\mu\sigma} \) muss nicht Null sein (z.B. Gravitation in der leeren Umgebung eines Sterns). Aufgrund der kontrahierten Bianchi-Identität \[ \sum_{\nu} \, D_{\nu} G^{\mu\nu} = 0 \] erfüllt der Energie-Impuls-Tensor automatisch die Kontinuitäts-Gleichung \[ \sum_{\nu} \, D_{\nu} T^{\mu\nu} = 0 \] |
Man kann die obigen Einsteinschen Feldgleichungen auch noch über einen anderen Weg erhalten: über ein Variationsprinzip! Das ist sehr beruhigend, denn unser obiger Weg war ja nur ein intelligentes Raten, und wenn man dasselbe Ergebnis auch auf einem ganz anderen Weg erreichen kann, so verstärkt das sicher unser Vertrauen. Allerdings muss man auch bei diesem alternativen Weg raten, aber nur einmal, und zwar ganz am Anfang: man muss eine naheliegende Formel für das Wirkungsfunktional des Gravitationsfeldes finden!
Die Ableitung des verallgemeinerten Gravitationsgesetzes aus einem Wirkungsprinzip erfolgte nicht durch Albert Einstein, sondern durch den Mathematiker David Hilbert, der zu Anfang des zwanzigsten Jahrhunderts einer der berühmtesten Mathematiker war (siehe auch Die Grenzen der Berechenbarkeit, Kapitel 1 ).

Quelle:
Wikimedia File:David Hilbert 1886.jpg, dort gemeinfrei
Das Variationsprinzip (auch Wirkungsprinzip oder
Prinzip der kleinsten Wirkung genannt) habe ich in
Quantenfeldtheorie und Eichfelder, Kapitel 3:
Die Quantisierung der klassischen Mechanik und für Felder in
Quantenfeldtheorie und Eichfelder, Kapitel 4:
Die kanonische Quantisierung des freien elektromagnetischen Feldes
ausführlich behandelt. Ich möchte mich deshalb hier relativ kurz fassen:
Man startet mit einem Wirkungsfunktional, das den dynamischen Feldern (Variablen) der Theorie reelle Zahlen zuordnet. Genauer: Man setzt bestimmte Randbedingungen für die Felder in Raum und Zeit voraus (die Felder müssen zumeist im Unendlichen in Raum und Zeit hinreichend schnell verschwinden) und betrachtet anschließend irgendwelche beliebigen (stetig-differenzierbaren) Felder als Funktion von Raum und Zeit, die diese Randbedingungen erfüllen (sie müssen aber noch keinerlei Bewegungsgleichung erfüllen). Das Wirkungsfunktional ordnet nun jeder dieser denkbaren Feldfunktionen über ein Raumzeit-Integral eine reelle Zahl zu – die sogenannte Wirkung.
Das Prinzip der kleinsten Wirkung besagt nun, dass die physikalischen Feldfunktionen genau diejenigen sind, bei denen das Wirkungsfunktional einen minimalen (genauer: einen stationären, d.h. in erster Ordnung konstanten) Wert für die Wirkung ergibt. Diese Felder erfüllen dann die Euler-Lagrange-Gleichungen – das sind dann die Bewegungsgleichungen der Felder, auch Feldgleichungen genannt.
Wie kommt es, dass ein solches Variationsprinzip möglich ist? Die Quantentheorie gibt dafür eine Begründung an: In der Feynman'schen Pfadintegralformulierung trägt jede denkbare Feldkonfiguration (nennen wir die \(A\) ) mit einem Summanden (genauer: Integralbeitrag) \[ \mathcal{D}A \; e^{ \frac{i}{\hbar} \, S[A] } \] zur Gesamt-Wahrscheinlichkeitsamplitude eines Messergebnisses bei. Dabei ist \( \mathcal{D}A \) ein geeigntetes Integrationsmaß (die Details dazu sind recht kompliziert) und \(S[A]\) ist die Wirkung der Feldkonfiguration \(A\) (d.h. \(A\) ist eine Funktion der Raumzeit, die Werte (Vektoren) im n-dimensionalen reellen Raum (die Feldwerte) liefert; ein Beispiel für \(A\) sind die elektromagnetischen Potentiale).
Wenn nun \( S[A] \) relativ groß im Vergleich zum Planchschen Wirkungsquantum \( \hbar \) ist ( → klassischer Grenzfall), so löschen sich die wild oszillierenden Quantenamplituden \( e^{ \frac{i}{\hbar} \, S[A] } \) der vielen denkbaren Feldkonfigurationen gegenseitig aus, außer bei den Feldern, die fast identische Wirkungen haben, d.h. bei denen \( S[A] \) sich kaum mit \(A\) ändert.
Das ist beispielsweise bei einem Minimum der Fall. Die Felder in der Nähe des Minimums von \(S[A]\) haben damit die größte Wahrscheinlichkeit, und im klassischen Grenzfall ist es dann gerade das Minimum von \(S[A]\), das übrig bleibt. Details dazu siehe Quantenfeldtheorie und Eichfelder, Kapitel 5: Pfadintegral-Quantisierung des freien elektromagnetischen Feldes.
Man sieht also, dass aus Sicht der Quantentheorie die Wirkung das zentrale Element der Theorie ist. Alleine deswegen ist es wichtig, ein Wirkungsfunktional für die Gravitation zu kennen, das die Einsteinschen Feldgleichungen reproduziert. Hier ist es:
|
Falls Sie Quantenfeldtheorie und Eichfelder, Kapitel 4:
Die kanonische Quantisierung des freien elektromagnetischen Feldes gelesen haben,
dann ist Ihnen vielleicht Folgendes aufgefallen:
Wir hatten dort vorausgesetzt, dass der Integrand der Wirkung nur die dynamischen Felder und deren ersten Ableitungen nach Raum und Zeit enthalten darf. Damit ist garantiert, dass die Feldgleichungen nur maximal zweite Ableitungen der Felder nach Raum und Zeit enthalten. Nun enthält der Ricci-Skalar \(R\) aber auch zweite Ableitungen der metrischen Matrixelemente! Man kann aber zeigen, dass hier diese zweiten Ableitungen für das Variationsprinzip irrelevant sind, so dass dennoch in den Feldgleichungen nur maximal zweite Ableitungen der Metrik auftreten. Details dazu findet man beispielsweise in Landau, Lifschitz: Lehrbuch der theoretischen Physik, Band II: Klassische Feldtheorie, §93 Die Wirkungsfunktion für das Gravitationsfeld.
Die minimale Wirkung findet man nun wie üblich, indem man für die metrischen Matrixelemente \( g_{\mu\nu} \) in der Wirkung \(S[g]\) den Ansatz \[ g_{\mu\nu} + \epsilon \eta_{\mu\nu} \] macht. Darin ist \( g_{\mu\nu} \) nun die metrische Matrix, für die die Wirkung minimal ist, und \( \epsilon \eta_{\mu\nu} \) ist die beliebige Abweichung (die Variation) davon. Das Minimum suchen wir über die Gleichung \[ \frac{d}{d \epsilon} S[g + \epsilon\eta] \bigg|_{\epsilon = 0} = 0 \] Aus Quantenfeldtheorie und Eichfelder, Kapitel 4 wissen wir, dass dies gerade die Funktionalableitung von \(S\) ist. Physiker verwenden auch gerne die formale Schreibweise \[ \frac{d}{d \epsilon} S[g + \epsilon\eta] \bigg|_{\epsilon = 0} = \] \[ =: \int \, d^{4}x \, \sum_{\mu\nu} \, \frac{\delta S}{\delta g^{\mu\nu}} \, \eta^{\mu\nu} = \] \[ =: \int \, dV \frac{1}{\sqrt{|\det{g}|}} \, \sum_{\mu\nu} \, \frac{\delta S}{\delta g^{\mu\nu}} \, \eta^{\mu\nu} \] Die konkrete (trickreiche) Rechnung möchte ich mir hier ersparen. Man findet sie z.B. in Landau, Lifschitz: Lehrbuch der theoretischen Physik, Band II: Klassische Feldtheorie, Kapitel XI Die Gleichungen des Gravitationsfeldes, oder auch in Sean M. Carroll: Lecture Notes on General Relativity, Kapitel 4 Gravitation sowie in G. 't Hooft: Introduction to General Relativity, Kapitel 8 The Action Principle. Das Ergebnis lautet: \[ \frac{d}{d \epsilon} S_{H}[g + \epsilon\eta] \bigg|_{\epsilon = 0} = \] \[ = \int \, dV \, \sum_{\mu\nu} \, G_{\mu\nu} \, \eta^{\mu\nu} \]
Der Vergleich mit oben ergibt \[ \frac{1}{\sqrt{|\det{g}|}} \, \frac{\delta S_H}{\delta g^{\mu\nu}} = G_{\mu\nu} \] Wir definieren nun den Energie-Impulstensor \(T_{\mu\nu}\) über die Gleichung: \[ \frac{d}{d \epsilon} S_{M}[g + \epsilon\eta] \bigg|_{\epsilon = 0} = \] \[ =: \int \, dV \, \sum_{\mu\nu} \, T_{\mu\nu} \, \eta^{\mu\nu} \] oder anders geschrieben \[ \frac{1}{\sqrt{|\det{g}|}} \, \frac{\delta S_M}{\delta g^{\mu\nu}} =: T_{\mu\nu} \] Damit ergibt \( \frac{d}{d \epsilon} S[g + \epsilon\eta] \big|_{\epsilon = 0} = 0 \) mit \( S[g] = \frac{c^{4}}{8 \pi G_{N}} S_{H}[g] + S_{M}[g] \) gerade die Einsteinschen Feldgleichungen \[ G_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, T_{\mu\nu} \] Übrigens ist die obige Gleichung \[ \frac{1}{\sqrt{|\det{g}|}} \, \frac{\delta S_M}{\delta g^{\mu\nu}} =: T_{\mu\nu} \] in der allgemeinen Relativitätstheorie eine ganz allgemeine Vorschrift, um aus einem Wirkungsfunktional für Materie den zugehörigen Energie-Impuls-Tensor zu definieren, der automatisch symmetrisch ist. Dass sich so die bekannten Energie-Impuls-Tensoren ergeben, kann man nachweisen. Wichtig ist, dass der Energie-Impuls-Tensor nur positive Energien (Massen) repräsentieren darf, d.h. in einem lokalen Inertialsystem muss \(T_{00}\) positiv sein. Negative Energien erlauben alle möglichen exotischen Lösungen für die Einsteinschen Feldgleichungen, z.B. Wurmlöcher oder Warp-Blasen – Star Treck Fans sind sicher begeistert, aber in der physikalischen Realität führen solche Lösungen zu großen Problemen, und außer in sehr extremen Situationen (Urknall, Quanten-Gravitation) sollten sie nicht vorkommen. ???
Die Einsteinschen Feldgleichungen \[ G_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, T_{\mu\nu} \] sind zunächst bei vorgegebenem Energie-Impuls-Tensor \( T_{\mu\nu} \) Gleichungen für 16 Matrixelemente \( G_{\mu\nu} \), die wiederum Funktionen der metrischen Matrix und ihrer ersten Ableitungen sind (die wiederum Funktionen von Raum und Zeit sind).
Da es sich um symmetrische Matrizen handelt, bleiben nur \( 4 + 3 + 2 + 1 = 10 \) unabhängige Gleichungen übrig. Da zusätzlich die 4 Gleichungen \[ \sum_{\nu} \, D_{\nu} G^{\mu\nu} = 0 \] gelten, haben wir schließlich nur 6 unabhängige Differentialgleichungen für die 10 Komponenten der metrischen Matrix.
Es bleiben also 4 Freiheitsgrade in der metrischen Matrix, die nicht durch die Einsteinschen Feldgleichungen festgelegt werden. Und das ist auch gut so, denn diese 4 Freiheitsgrade brauchen wir, um Koordinatenwechsel und damit Bezugssystemwechsel der 4 Raum-Zeit-Koordinaten zu ermöglichen. Es soll nämlich nicht die metrische Matrix selbst, sondern die Metrik \( g(u,v) \) in beliebigen Koordinaten bestimmbar sein. Analog ändert sich auch oben die Wirkung \( S[g] \) nicht, wenn man \(g\) nur in anderen Koordinaten ausdrückt. Das gesuchte Minimum von \( S[g] \) ist also eher ein Tal, das in Richtung der \(g\)'s verläuft, die durch Koordinatenwechsel ineinander umwandelbar sind.
Tatsächlich kann man zeigen, dass die Einsteinschen Feldgleichungen ein wohldefiniertes Anfangswertproblem für die Metrik ergeben. Dazu gibt man zunächst eine raumartige 3-dimensionale Hyperfläche in der Raumzeit vor. Raumartig bedeutet, dass man in jedem Punkt immer ein lokales Inertialsystem wählen kann, so dass die unmittelbaren Nachbarpunkte als gleichzeitig angesehen werden können (den Begriff der Gleichzeitigkeit hatten wir oben bereits näher betrachtet). Auf dieser Hyperfläche soll nun die Metrik und die Ableitung der Metrik in eine nicht-tangentiale Richtung zur Hyperfläche vorgegeben sein – das sind die Anfangsbedingungen. Die Veränderung der Metrik in Richtung weg von der Hyperfläche entspricht in gewissen lokalen Bezugssystemen der zeitlichen Entwicklung. Diese zeitliche Entwicklung lässt sich nun mit Hilfe von 6 der 10 Einsteinschen Feldgleichungen bestimmen.
Die übrigen 4 Gleichungen dagegen dienen als Nebenbedingungen, die das Bezugssystem auf der Hyperfläche einschränken – das braucht man, um eine Zeitkoordinate identifizieren zu können, denn man kann nicht beliebige Kombinationen von metrischer Matrix und deren Ableitungen auf der Hyperfläche vorgeben. Der Formalismus weist große Ähnlichkeiten mit dem Lagrange-Formalismus bei Eichtheorien auf, bei dem auch nicht alle Lagrange-Gleichungen eine zeitliche Entwicklung von Funktionen beschreiben (siehe Quantenfeldtheorie und Eichfelder, Kapitel 4: Die kanonische Quantisierung des freien elektromagnetischen Feldes, man betrachte dort insbesondere die kanonisch konjugierte Impulskomponente \( \pi^{0} \)). Die Freiheit, das Koordinatensystem und damit das Raum-Zeit-Bezugssystem zu wechseln, entspricht der Eichfreiheit bei Eichtheorien wie dem Elektromagnetismus.
Man kann hier noch sehr viel weiter ins Detail gehen, doch das würde den Rahmen dieses Kapitels sprengen. Stattdessen wollen wir noch auf zwei Veranschaulichungen der Einsteinschen Feldgleichungen eingehen, die ihren physikalischen Inhalt verdeutlichen.
Die erste Veranschaulichung stammt von Richard Feynman. Man findet sie in Feynmans Vorlesungen über Physik, Band II Elektromagnetismus und Struktur der Materie in Kapitel 42 Der gekrümmte Raum sowie in The Feynman Lectures on Gravitation (Westview Press, Boulder, Colorado, 2002). Feynman legt dabei den Schwerpunkt auf die Krümmung des Raumes (und nicht der Raumzeit):
|
Anschauliche Formulierung des Einsteinschen Gravitationsgesetzes nach Richard Feynman: Greifen wir in einem materieerfüllten Raumgebiet eine Kugel heraus, die genügend klein ist, so dass die Dichte \(\rho\) der gravitationserzeugenden Materie-Energie-Verteilung innerhalb praktisch konstant ist. Dann ist der sogenannte Exzessradius für die Kugel proportional zur in ihr enthaltenen Masse bzw. Energie (über den Druck sagt Feynman hier nichts). Der Exzessradius \( r_{e} \) ist dabei der Unterschied zwischen dem Radius \( r \), den man aufgrund der gemessenen Kugeloberfläche \( A \) nach der euklidischen Formel \[ A = 4 \pi r^{2} \] berechnet, und dem tatsächlich gemessenen Kugelradius \( r_{g} \), also \[ r_{e} = r - r_{g} \] Damit beschreibt der Exzessradius die Abweichung der tatsächlichen räumlichen Geometrie von der gewohnten euklidischen Geometrie. Es gilt \[ r_{e} = \frac{G_{N}}{3 c^{2}} \, M \] mit der Masse \( M \) innerhalb der Kugel. Der Exzessradius der Erde beträgt beispielsweise 1,5 Millimeter, der der Sonne etwa einen halben Kilometer. Diese Formulierung ist gleichwertig zum Einsteinschen Gravitationsgesetz, wenn man sie für Kugeln beliebiger Geschwindigkeit (unterhalb von \(c\)) voraußetzt. |
Eine zweite sehr schöne Veranschaulichung inklusive Herleitung, die den Fokus auf die
Krümmung der Raum-Zeit (nicht nur des Raumes) legt, findet man in
John Baez, Emory Bunn: The Meaning of Einstein's Equation, arXiv:gr-qc/0103044:
Man startet mit einer sehr kleinen (infinitesimalen) kugelförmigen Anordnung von frei beweglichen winzigen Staubpartikeln. Die Staubpartikel sollen eine so geringe Masse haben, dass ihr Gravitationsfeld vernachlässigt werden kann. Das Volumen dieser Anordnung zum Zeitpunkt \(t\) wollen wir mit \( V(t) \) bezeichnen.
Zum Startzeitpunkt \( t = 0 \) sollen sich die Staubpartikel relativ zueinander
nicht bewegen, d.h.
\[
\frac{d}{dt} V(t) \bigg|_{t = 0} = 0
\]
Diese Aussage macht nur Sinn, weil wir von sehr
kleinen Anfangs-Abständen zwischen den Staubpartikeln ausgehen, so dass sich die Geschwindigkeiten
in eindeutiger Weise in erster Ordnung
über infinitesimale Parallelverschiebungen miteinander vergleichen lassen.
Bei größeren Abständen ist ein solcher Vergleich ja wegen der Wegabhängigkeit der Parallelverschiebung
nicht möglich.
Nach einer kurzen (infinitesimalen) Zeitspanne wird sich die Position der Staubpartikel
relativ zueinander verändern, sofern ein Gravitationsfeld vorhanden ist.
Im Gravitationsfeld der Erde werden beispielsweise die weiter unten liegenden Staubpartikel
etwas stärker angezogen als die weiter oben liegenden. Die Staubpartikel beschleunigen
relativ zueinander. Das ist genau die Gezeitenwirkung der Gravitation,
die wir oben im Zusammenhang mit der equation of geodesic deviation
bei der Motivation der Einsteinschen Feldgleichungen betrachtet hatten.
Man kann sagen, dass letztlich in dieser equation of geodesic deviation
der physikalische Kern des Einsteinschen Gravitationsgesetzes steckt.
Es wundert daher nicht, dass wir mit dieser Gleichung als Ausgangspunkt wieder zu einer
Beschreibung der Gravitation gelangen werden, die gleichwertig zum Einsteinschen Gravitationsgesetz ist.
Durch die Beschleunigung der Staubpartikel zum Startzeitpunkt verändert sich auch das Volumen \(V(t)\) der kugelförmigen Anordnung der Staubpartikel. Die Volumenänderung zum Startzeitpunkt ist zwar Null, da die Staubpartikel zu diesem Zeitpunkt sich relativ zueinander nicht bewegen, aber die zeitliche Änderung dieser Volumenänderung (also die zweite zeitliche Ableitung des zeitabhängigen Volumens) ist nicht Null, denn die Staubpartikel beschleunigen relativ zueinander. Mit Hilfe der equation of geodesic deviation kann man herleiten:
|
Anschauliche Formulierung des Einsteinschen Gravitationsgesetzes nach John Baez und Emory Bunn: Für eine infinitesimale kugelförmige Anordnung (eine Wolke) winziger Testpartikel, die sich im kugelförmigen Volumen \(V(t)\) in einem äußeren Gravitationsfeld befinden und die sich zum Startzeitpunkt \( t = 0 \) relativ zueinander in Ruhe befinden, sodass \[ \frac{d}{dt} V(t) \bigg|_{t = 0} = 0 \] ist, gilt folgende Gleichung für die Änderung des Volumenwachstums (oder der Volumenschrumpfung) zur Startzeit Null: \[ \frac{d^{2}}{dt^{2}} V(t) \bigg|_{t = 0} = \] \[ = - \frac{4 \pi G_{N}}{c^{4}} \, V(0) \, \sum_{\mu} T^{\mu\mu} \] Da wir \(T^{00}\) als Energie-Massen-Dichte und \(T^{kk}\) als k-Komponente der Flächenstromdichte der k-ten Impulskomponente (also als Druck in k-Richtung) interpretieren können, besagt diese Gleichung in Worten:
Die Test-Kugelwolke selbst soll so leicht sein, dass sie praktisch kein Gravitationsfeld erzeugt. Die gravitationserzeugende Materie-Energie-Verteilung im Kugelvolumen soll ausschließlich über die Gravitation auf die Wolke der Testpartikel einwirken, also keine direkten Zusammenstöße oder Ähnliches. Diese Formulierung ist gleichwertig zum Einsteinschen Gravitationsgesetz, wenn man sämtliche kleinen Kugelwolken mit allen möglichen Anfangsgeschwindigkeiten in Betracht zieht, also alle in allen möglichen lokalen Inertialsystemen ruhenden Kugelwolken.
|
Das negative Vorzeichen zeigt, dass eine positive Energie-Massendichte und ein positiver Druck
ein Schrumpfen der Kugelwolke bewirken – Gravitation ist eine anziehende Kraft.
Beim Druck kommt uns das merkwürdig vor, aber es geht hier um die rein gravitative Wirkung
des Drucks. Die Testpartikel der Kugelwolke sollen nicht direkt durch den Druck der
gravitationserzeugenden Materie beeinflusst werden, sondern nur durch deren Gravitationskraft!
Normalerweise spielt der Druck für die Gravitation keine Rolle. In extremen Situationen oder auch bei Strahlung ist das anders. In einem Neutronenstern ist beispielsweise der Druck aufgrund des Pauliprinzips enorm groß – nur so kann er den endgültigen Kollaps des Sterns verhindern. Der Druck erzeugt hier einen wesentlichen Anteil der Gesamtgravitation des Sterns!
Im leeren (aber nicht gravitationsfreien) Raum, z.B. außerhalb eines Sterns, ist die rechte Seite der Gleichung gleich Null. Somit ist auch \[ \frac{d^{2}}{dt^{2}} V(t) \bigg|_{t = 0} = 0 \] d.h. das Volumen der kleinen Test-Kugelwolke ändert sich nicht (denn \( \frac{d}{dt} V(t) \bigg|_{t = 0} \) war ja ebenfalls Null). Die Wolke kann aber immer noch aufgrund lokal unterschiedlich starker Gravitationskräfte verzerrt werden, z.B. in einer Richtung gedehnt und in den beiden anderen Richtungen gestaucht werden, so dass ein volumengleicher Ellipsoid entsteht – man spricht von Gezeitenkräften (engl.: tidal forces).
Die obige Überlegung ermöglicht es auch, im Krümmungstensor den Anteil des Ricci-Tensors und den des Weyl-Tensors (siehe oben) anschaulich zu unterscheiden: Im Einsteinschen Gravitationsgesetz steht der Ricci-Tensor, der für die Volumenänderung unserer kleinen Testwolke verantwortlich ist. Diese Volumenänderung wird durch Energiedichte und Druck am Ort der Wolke bewirkt – genau das sagt das Einsteinschen Gravitationsgesetz. Der Weyl-Tensor dagegen besagt, wie sich die Testwolke bei konstantem Volumen im Gravitationsfeld aufgrund der Gezeitenkräfte verformt. In materiefreien Raumbereichen ist der Ricci-Tensor Null, nicht aber der Weyl-Tensor!
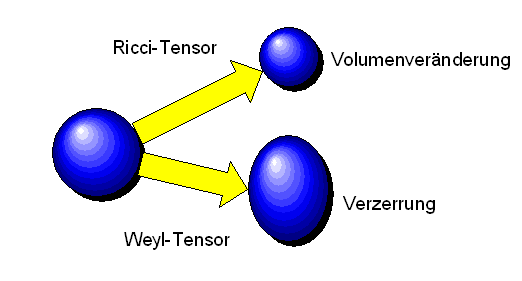
Zum Abschluss wollen wir noch einen Zusatz diskutieren, den man in den Einsteinschen Feldgleichungen anbringen kann: die kosmologische Konstante \( \Lambda \). Mit kosmologischer Konstante lauten die Einsteinschen Feldgleichungen: \[ G_{\mu\nu} = \frac{8 \pi G_{N}}{c^{4}} \, T_{\mu\nu} + \Lambda \, g_{\mu\nu} \] Man kann sich vorstellen, dass zum Energie-Impuls-Tensor \( T_{\mu\nu} \) ein Term \[ \frac{c^{4}}{8 \pi G_{N}} \, \Lambda \, g_{\mu\nu} \] hinzukommt. Diesen Term kann man als Energie-Impuls-Tensor des Vakuums interpretieren. Demnach besitzt das Vakuum eine Energiedichte \[ \frac{c^{4}}{8 \pi G_{N}} \, \Lambda \] und einen negativen Druck \[ - \frac{c^{4}}{8 \pi G_{N}} \, \Lambda \] (das negative Vorzeichen stammt von den räumlichen Diagonalelementen der metrischen Matrix).
Die Formel \[ \frac{c^{4}}{8 \pi G_{N}} \, \Lambda \, g_{\mu\nu} \] für den Energie-Impuls-Tensor des Vakuums garantiert, dass unter den lokalen Inertialsystemen keines als ruhend ausgezeichnet ist, denn in allen gleichförmig gegeneinander bewegten lokalen Ruhe-Inertialsystemen hat der Vakuum-Energie-Impuls-Tensor dieselbe Form (ein Boost verändert ja die Minkowski-Metrik nicht).
Setzen wir den Vakuum-Energie-Impuls-Tensor in unsere obige anschauliche Formulierung des Gravitationsgesetzes mit Hilfe der kleinen Test-Kugelwolke ein, so erhalten wir für das Volumen dieser Wolke \[ \frac{d^{2}}{dt^{2}} V(t) \bigg|_{t = 0} = \] \[ = - \frac{4 \pi G_{N}}{c^{4}} \, V(0) \, \sum_{\mu} T^{\mu\mu} = \] \[ = - \frac{4 \pi G_{N}}{c^{4}} \, V(0) \, (- 2) \, \frac{c^{4}}{8 \pi G_{N}} \, \Lambda = \] \[ = \Lambda \, V(0) \] Das Kugelvolumen wächst also bei positiver kosmologischer Konstante, d.h. der Vakuum-Energie-Impuls-Tensor wirkt abstoßend! Das liegt daran, dass der negative Druck des Vakuums zwar denselben Betrag wie die positive Vakuum-Energiedichte hat, aber wegen der drei Raumdimensionen auch dreimal gezählt wird und so die positive Energiedichte mehr als kompensiert.
Jede kleine Kugel aus Testteilchen dehnt sich bei einer positiven kosmoligischen Konstanten letztlich beschleunigt aus. Man kann dies so interpretieren, dass sich der Raum insgesamt beschleunigt ausdehnt; ein immer schneller expandierendes Universum ist die Folge, sofern die Wirkung der kosmologischen Konstante gegenüber dem Energie-Impuls-Tensor der Materie dominiert.
Seit 1998 hat man aufgrund der Messung von Helligkeit und Rotverschiebung weit entfernter thermonuklearer Sternexplosionen (sogenannte Supernovae vom Typ Ia) klare Hinweise darauf, dass sich unser Universum tatsächlich beschleunigt ausdehnt. Es ist also sehr wahrscheinlich, dass die kosmologische Konstante in unserer Welt tatsächlich positiv ist und der leere Raum tatsächlich eine entsprechende Energiedichte und negativen Druck besitzt. Man spricht auch von der Dunklen Energie, die den Raum gleichförmig durchdringt. Ursache könnten sogenannte Vakuum-Quantenfluktuationen sein, aber ob das so ist, bleibt unklar, denn Abschätzungen der Energie dieser Vakuum-Quantenfluktuationen liefern viel zu große Werte. Die Dunkle Energie ist damit eines der großen ungelösten Mysterien unseres Universums.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 08 September 2023