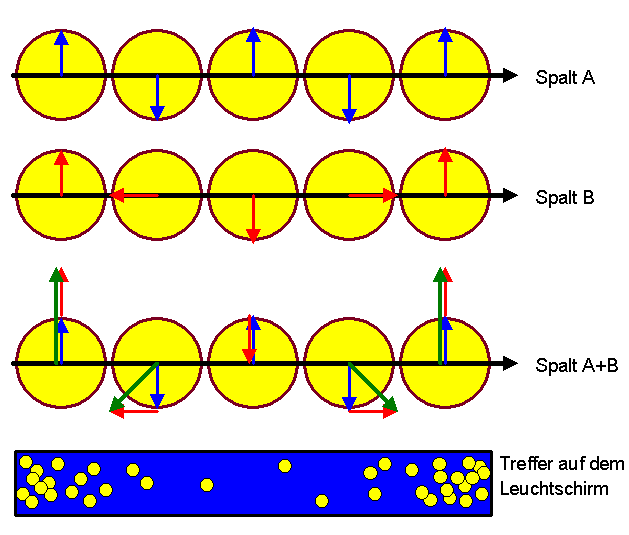
Zusammenfassung des Buchkapitels:
In der Quantenfeldtheorie müssen wir Wahrscheinlichkeitspfeile (beispielsweise für die Streumatrix) berechnen. Für den Umgang mit Wahrscheinlichkeits-Pfeilen gelten die folgenden Regeln, die wir bereits in Kapitel 2.3 kurz angesprochen hatten:
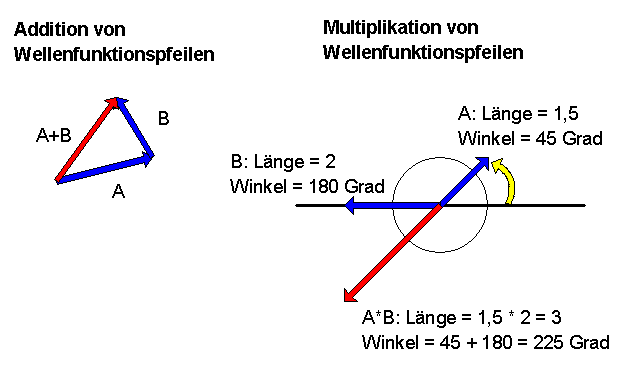
Dort, wo wir normalerweise einzelne Wahrscheinlichkeiten addieren würden, werden in der Quantentheorie statt dessen also Pfeils aufaddiert.

Dort, wo wir normalerweise einzelne Wahrscheinlichkeiten multiplizieren würden, werden in der Quantentheorie statt dessen Pfeils multipliziert. Die Pfeilmultiplikation entspricht dabei der Multiplikation komplexer Zahlen, also einer Drehstreckung: Die Pfeillängen werden multipliziert und die Drehwinkel zur x-Achse werden addiert:
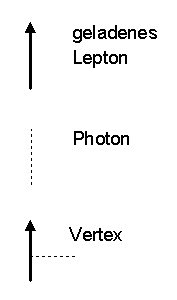
Welche Teilschritt-Typen möglich sind, hängt von der betrachteten
Wechselwirkung ab. In der Quantenfeldtheorie der elektromagnetischen Wechselwirkung
(Quantenelektrodynamik QED) treten nur die folgenden
drei grundlegenden Teilschritt-Typen auf:
Wir wollen diese drei Teilschritt-Grundtypen durch die folgenden graphischen Symbole darstellen (die Zeit soll dabei nach oben laufen; der Pfeil für Anti-Lepton-Linien zeigt gegen die Zeitrichtung):
Die Teilschritt-Typen lassen sich nun zu komplizierteren
Diagrammen zusammensetzen. Die so
entstehenden Diagramme werden Feynmangraphen genannt,
zu Ehren des Physikers Richard P. Feynman (1918 bis 1988), der sie erfunden hat.

Quelle:
Wikipemia Commons File:RichardFeynman-PaineMansionWoods1984 copyrightTamikoThiel bw.jpg, Copyright Tamiko Thiel 1984,
CC BY-SA 3.0 DEED
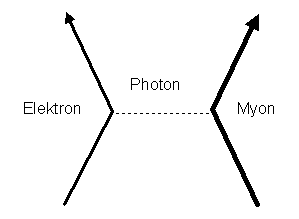
Hier ist als Beispiel der einfachste Feynmangraph
für die elastische Elektron-Myon-Streuung,
bei der ein Elektron und ein Myon aufeinander zufliegen, ein virtuelles Photon austauschen
und wieder auseinanderfliegen:
Bei dem ein- und auslaufenden Elektron und Myon
stehen Energie \(E\) und Impuls \(\boldsymbol{p}\) in
einer festen Beziehung miteinander, so wie es die Formel
\[
E^{2} = (mc^{2})^{2} + (\boldsymbol{p}c)^{2}
\]
angibt.
Diese Formel gilt allgemein für reelle Teilchen (d.h. Teilchen, deren Energie und Impuls messbar ist,
da sie lange genug leben).
Für das virtuelle Photon gilt diese Energie-Impuls-Beziehung nicht (denn das virtuelle Photon lebt nur kurz, so dass die Energie-Zeit-Unschärfe Abweichungen erlaubt)! Im Schwerpunktsystem wäre beispielsweise die Energie des Photons gleich Null, da es in diesem Bezugssystem keine Energie zwischen Elektron und Myon überträgt (Elektron und Myon behalten im Schwerpunktsystem ihre Energie). Sein Impuls wäre aber ungleich Null, da Elektron und Myon nachher in andere Richtungen fliegen als vorher und das Photon demnach Impuls zwischen ihnen überträgt.
Zu jedem der drei Teilschritt-Typen gehört ein Wahrscheinlichkeitspfeil. Wenn wir den Spin weglassen, so gehört zu einer inneren Linie (wie der obigen virtuellen Photonlinie) im Wesentlichen ein Faktor, nämlich \[ \frac{1}{E^{2} - (\boldsymbol{p}c)^{2} - (mc^{2})^{2}} \] Dieser Term hat etwas mit der Klein-Gordon-Wellengleichung zu tun, die die Fortbewegung von relativistischen Teilchen beschreibt (mehr dazu siehe unten bei den Zusatzinformationen). Dabei ist der Term \[ E^{2} - (\boldsymbol{p}c)^{2} \] in der speziellen Relativitätstheorie unabhängig vom Bezugssystem, obwohl \(E\) und \(\boldsymbol{p}\) einzeln vom Bezugssystem abhängen. Der Faktor einer inneren Linie ist damit umso größer, je genauer Energie und Impuls des entsprechenden virtuellen Teilchens die Beziehung \( E^{2} = (mc^{2})^{2} + (\boldsymbol{p}c)^{2} \) erfüllen, wie sie für ein freies Teilchen gilt.
Zu einem Vertex gehört (ohne Spin) ebenfalls im Wesentlichen ein Faktor, nämlich die elektrische Ladung des Teilchens (das das Photon aussendet) in natürlichen Einheiten. Das Quadrat der elektrischen Elementarladung \(e\) lautet in natürlichen Einheiten \[ \alpha := k \frac{e^{2}}{\hbar c} \] mit \[ k = \frac{1}{4 \pi \epsilon_{0}} \] Man nennt \(\alpha\) auch die Kopplungskonstante (Feinstrukturkonstante) der elektromagnetischen Wechselwirkung. Entsprechend ist \(\alpha\) eine dimensionslose Zahl. Sie ist ein Maß für die Stärke der Wechselwirkung und hat ungefähr den Wert \[ \alpha \approx \frac{1}{137} \] Damit ist sie deutlich kleiner als Eins. Das ist die Grundvoraussetzung dafür, dass wir Störungstheorie anwenden und damit Feynmangraphen benutzen können.
Es gibt noch unendlich viele weitere Graphen (entsprechend unendlich vieler virtueller Teilchen) für die obige Wechselwirkung von Elektron und Myon. Hier zwei Beispiele:
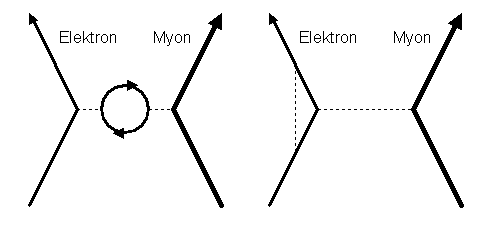
Dabei ist der Impuls der virtuellen Teilchen nicht unbedingt durch
das ein- und auslaufende Elektron und Myon festgelegt, und es muss
über alle möglichen Impulse der virtuellen Teilchen summiert (integriert) werden.
Das Problem dabei ist, dass sich so ein Summenpfeil unendlicher Länge ergibt.
Erst im Jahr 1948 konnte dieses Problem durch
Julian Schwinger, Sin-Hiro Tomonaga
und Richard P. Feynman gelöst werden (mehr dazu
in Kapitel 6.3).
Da bei der elektromagnetischen Wechselwirkung jeder Vertex einen Faktor \[ \sqrt{\alpha} \approx 0,085 \] beiträgt, sind kompliziertere Graphen mit vielen Vertices stark unterdrückt, so dass oft schon der einfachste Graph ausreicht. Bei der starken Wechselwirkung wird das anders sein!
Nun können wir die Frage lösen, warum gewisse Reaktionen möglich sind, andere dagegen nicht:
Ein weiteres Beispiel ist das Aufeinandertreffen eines Elektrons und eines Positrons:
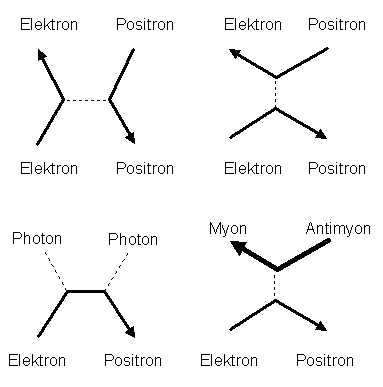
Einige mögliche Feynmangraphen für die elektromagnetische
Wechselwirkung zwischen einem Elektron (Pfeil in Zeitrichtung, also nach oben) und einem Positron
(Pfeil gegen die Zeitrichtung, also nach unten). Elektron und Positron können elastisch aneinander streuen, zu zwei
Photonen zerstrahlen oder (bei genügend Energie) andere Teilchen-Antiteilchen-Paare erzeugen.
Es ist aber nicht möglich, dass
sich Elektron und Positron vernichten und
daraus ein Elektron plus ein Antimyon entsteht, denn es gibt keinen elektromagnetischen Vertex
zwischen einem Elektron, einem Myon und einem Photon.
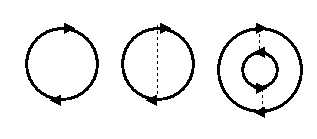
Noch ist noch ein Beispiel: die Feynmangraphen für das Vakuum,
also für den fluktuierender See aus virtuellen Teilchen-Antiteilchen-Paaren und
virtuellen Photonen.
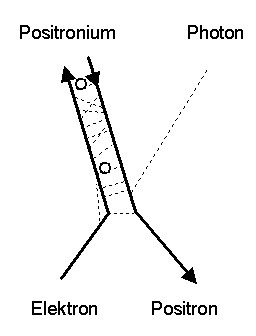
Ein weiteres Beispiel:
die Bildung von Positronium, bei dem
Elektron und Positron einen atomähnlichen Bindungszustand eingehen,
der im Mittel nach \(1,25 \cdot 10^{-10}\) Sekunden zerstrahlt, da sich Elektron und Positron schließlich
gegenseitig vernichten:
Mit unserem obigen Bausatz für Feynmangraphen
können wir die elektromagnetische Wechselwirkung
von geladenen Fermionen und Photonen sehr präzise beschreiben
(die entsprechende Quantenfeldtheorie heißt
Quantenelektrodynamik (QED)). Nun gilt es, den Bausatz zu erweitern
und auch die starke und schwache Wechselwirkung einzubeziehen.
a) über die elektromagnetischen Kopplungskonstante α
b) Potentiale und Propagatoren
Da \( \sqrt{\alpha} \) die Wahrscheinlichkeitsamplitude für den Vertex-Teilschritt in Feynmangraphen ist, kann man \(\alpha\) als die Wahrscheinlichkeit dafür interpretieren, dass ein Teilchen mit einer Elementarladung ein Photon aussendet. Je größer diese Wahrscheinlichkeit ist, umso stärker wird beispielsweise die elektrische Kraft zwischen zwei statischen Ladungen sein. Das wird deutlich, wenn wir das Coulombsche Kraftgesetz entsprechend umschreiben: \[ F = k \, \frac{q_{1} q_{2}}{r^{2}} = \] \[ = k \, \frac{e^{2}}{\hbar c} \, \frac{\hbar c}{e^{2}} \, \frac{q_{1} q_{2}}{r^{2}} = \] \[ = \alpha \, \frac{q_{1} q_{2}}{e^{2}} \, \frac{\hbar c}{r^{2}} \] Wenn wir hier den Abstand \(r\) in Fermi angeben und verwenden, dass \( \hbar c \) ungefähr 200 MeV fm ist, so ergibt der Term \( \frac{\hbar c}{r^{2}} \) eine Kraft in der Einheit MeV/fm. Diese Kraft wird nun noch mit zwei dimensionslosen Vorfaktoren multipliziert: mit der Größe der elektrischen Ladungen, angegeben als Vielfache der Elementarladung \( q_{1}/e \) und \( q_{2}/e \), sowie mit dem Vorfaktor \( \alpha \approx 1/137 \), der die allgemeine Stärke der elektromagnetischen Wechselwirkung bestimmt.
Auch das Newtonsche Gravitationsgesetz kann man ähnlich schreiben, wenn man die Planckmasse verwendet – mehr dazu in Kapitel 7.2 (Zusatzinfos).
(für fortgeschrittene Leser mit mathematisch-physikalischem Hintergrundwissen)
Zu einer inneren Teilchenlinie in einem Feynmangraph gehört die Wahrscheinlichkeitsamplitude \[ \frac{1}{E^{2} - (\boldsymbol{p}c)^{2} - (mc^{2})^{2}} \] (siehe oben), wobei wir Komplikationen aufgrund des Teilchenspins hier weglassen. Woher kommt dieser sogenannte Propagatorterm?
Der Propagatorterm hat seinen Ursprung in der Klein-Gordon-Gleichung, die wir in den Zusatzinfos zu Kapitel 5.1 bereits kennengelernt haben (die Bedeutung der relativistischen Vierervektor-Schreibweise ist dort und in Kapitel 3.2 erklärt): \[ g(\hat{P},\hat{P}) \, \phi(x) = (mc)^{2} \, \phi(x) \] mit dem Raum-Zeit-Punkt \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} \] sowie \[ g(\hat{P},\hat{P}) = - \hbar ^{2} \, g(D,D) = \] \[ = - \hbar ^{2} \left( \frac{1}{c^2} \frac{d^2}{dt^2} - \frac{d^2}{d\boldsymbol{x}^2} \right) \] Wie bei der Klein-Gordon-Gleichung üblich schreiben wir hier \(\phi(x)\) statt \(\psi;(x)\). Wichtig war, dass bei einer ebenen Welle \[ \phi_{p}(x) := e^{- \frac{i}{\hbar} \, g(p,x)} \] die Beziehung \[ \hat{P} \, \phi_p(t,\boldsymbol{x}) = p \, \phi_p(t,\boldsymbol{x}) \] gilt. Die ebene Welle ist daher eine Lösung der Klein-Gordon-Gleichung, wobei sich \( g(p,p) = (mc)^{2} \) ergibt, so wie das bei einem freien Teilchen auch sein muss.
Im Folgenden wollen wir die Schreibweise etwas vereinfachen und zur üblichen Teilchenphysik-Schreibweise übergehen, indem wir alle dimensionsbehafteten Größen wie Energien, Massen, Impulse, Längen etc. in Energieeinheiten (z.B. MeV) angeben, so dass wir \(\hbar\) und \(c\) in den Formeln weglassen können (siehe Kapitel 3.3 über natürliche Maßeinheiten). Mit \(\hbar\) und \(c\) können wir die Größen dann jederzeit von MeV in Größen wie fm etc. umrechnen.
Außerdem ist es üblich, die Minkowski-Metrik \(g(a,b)\) zweier Vierervektoren einfach kurz als \( a b \) zu schreiben. Der Propagatorterm lautet dann einfach \[ \frac{1}{p^{2} - m^2} = \frac{1}{E^{2} - \boldsymbol{p}^{2} - m^2} \] und für freie Teilchen gilt \[ p^{2} = E^{2} - \boldsymbol{p}^{2} = m^{2} \] Die freie Klein-Gordon-Gleichung lautet entsprechend \[ \hat{P}^{2} \, \phi(x) = m^{2} \, \phi(x) \] mit \[ \hat{P}^{2} = - \left( \frac{d^2}{dt^2} - \frac{d^2}{d\boldsymbol{x}^2} \right) \] (d.h. der Differentialoperator \(\hat{P}\) leitet nach den Raumzeit-Koordinaten \(x\) ab).
Für die folgende Diskussion ist es nützlich, nicht die freie Klein-Gordon-Gleichung zu betrachten, sondern die Klein-Gordon-Gleichung mit einer von außen vorgegebenen Quelle \( j(x) \). Diese Gleichung lautet
|
Klein-Gordon-Gleichung mit äußerer Quelle: \[ \left( -\hat{P}^{2} + m^{2} \right) \, \phi(x) = j(x) \] |
Eine Gleichung diesen Typs (mit Masse \(m = 0\)) erhält man beispielsweise für die
Komponenten \(A^{\mu}(x)\) des elektromagnetischen
Vierer-Potentials in der Lorentz-Eichung bei von außen vorgegebenem Viererstrom.
Insbesondere ergibt sich eine solche Gleichung für das elektrische Potential \(\phi(x)\),
wobei dann \(j(x)\) die elektrische Ladungsdichte ist (siehe
Zusatzinfos zu Kapitel 1.4 sowie
Quantenfeldtheorie und Eichfelder, Kapitel 4).
Die obige Gleichung ist also zunächst eine klassische Gleichung für ein skalares Potential,
das von einer Ladungsdichte \(j(x)\) erzeugt wird.
Die Verbindung zur Quantentheorie ergibt sich dann über die Teilcheninterpretation ebener Wellen.
In der Gleichung oben steht links schon fast so etwas wie der Kehrwert des Propagatorterms \[ \frac{1}{p^{2} - m^2} \] und tatsächlich hat der Propagatorterm etwas mit dem formalen Invertieren des Operators links zu tun – was gleichbedeutend damit ist, die Gleichung formal zu lösen. Genau das wollen wir jetzt tun. Dazu verwenden wir, dass jede Lösung der obigen linearen Differentialgleichung in der folgenden Form geschrieben werden kann:
| \[ \phi(x) = \varphi(x) + \int d^{4}x' \, G(x - x') \, j(x') \] |
Dabei ist \( G(x - x') \) irgendeine noch zu bestimmende Funktion
(auch Green'sche Funktion genannt) und
\( \varphi(x) \) ist eine Lösung der freien Klein-Gordon-Gleichung ohne Quelle \(j(x)\), d.h.
es ist
\[
\left( -\hat{P}^{2} + m^{2} \right) \, \varphi(x) = 0
\]
Setzen wir die obige Darstellung für \(\phi(x)\) in die Klein-Gordon-Gleichung
mit Quelle \(j(x)\) ein, so ergibt sich
die Bedingung
\[
j(x) =
\left( -\hat{P}^{2} + m^{2} \right) \, \phi(x) =
\]
\[ =
\left( -\hat{P}^{2} + m^{2} \right)
\]
\[
\left[
\varphi(x) +
\int d^{4}x' \, G(x - x') \, j(x')
\right]
=
\]
\[ =
\int d^{4}x' \,
\left[
\left( -\hat{P}^{2} + m^{2} \right) \,
G(x - x') \right] \, j(x')
\]
Mit Hilfe der vierdimensionalen Delta-Funktion \( \delta(x - x') \) können wir diese Bedingung
an die Funktion \( G(x - x') \) auch schreiben als
| \[ \left( -\hat{P}^{2} + m^{2} \right) \, G(x - x') = \delta(x - x') \] |
wobei \( \delta(x - x') \) die Bedingung
\[
\int d^{4}x' \, \delta(x - x') \, j(x') = j(x)
\]
erfüllt.
Man kann sich die Delta-Funktion als sehr schmalen und hohen Berg um \( x - x' = 0 \) herum vorstellen,
der das Raumzeit-Volumen 1 umfasst. Der Grenzfall des unendlich schmalen und hohen Berges ergibt die obige Formel.
Mathematiker sprechen hier genauer von Distributionen. Mehr dazu in
Quantenfeldtheorie und Eichfelder, Kapitel 4.
Die obige Gleichung für \(G\) entspricht der Klein-Gordon-Gleichung mit der ganz speziellen Ladungsverteilung \[ j(x) = \delta(x) \] (wir können \(x' = 0\) setzen, indem wir die Ladungsverteilung entsprechend verschieben; \(\hat{P}^{2}\) wirkt ja nur auf \(x\)).
Das bedeutet anschaulich, dass für einen winzigen Moment zur Zeit \(t = 0\) eine punktförmige Ladung am Ort \(\boldsymbol{x} = 0\) gleichsam aufblitzt und wieder verschwindet.
Dieses Aufblitzen der Ladung wird Wellen auslösen, so wie man Wellen auf einer Wasseroberfläche auslöst, indem man einen Stein hineinwirft. Die Funktion \(G(x)\) beschreibt die Ausbreitung dieser Wellen in Raum und Zeit, die wir auch als Elementarwellen bezeichnen können, da sich durch ihre Überlagerung alle anderen Lösungen der Gleichung zusammensetzen lassen.
Also beschreibt \(G(x - x')\) die Ausbreitung von Elementarwellen, die durch das Aufblitzen einer Ladung zur Zeit \(t'\) am Ort \(\boldsymbol{x}'\) entstanden sind. Man sagt auch, \(G(x - x')\) beschreibt die Propagation der bei \(x'\) entstandenen Elementarwelle zum Raumzeitpunkt \(x\) hin. Entsprechend nennt man \(G\) auch den Propagator.
Um den Propagator \(G\) auszurechnen, schreiben wir ihn in Form eines Fourierintegrals: \[ G(x - x') = N \int d^{4}p \, \tilde{G}(p) \, e^{- i p (x - x')} \] mit dem Normierungsfaktor \[ N = \frac{1}{(2 \pi )^{4}} \] und setzen ihn in die Propagatorgleichung \[ \left( -\hat{P}^{2} + m^{2} \right) \, G(x - x') = \delta(x - x') \] ein, wobei wir beachten, dass der Operator \(\hat{P}^{2}\) nach \(x\) ableitet: \[ \left( -\hat{P}^{2} + m^{2} \right) \, G(x - x') = \] \[ = N \int d^{4}p \, \tilde{G}(p) \, \left( -\hat{P}^{2} + m^{2} \right) \, e^{- i p (x - x')} = \] \[ N \int d^{4}p \, \tilde{G}(p) \, \left( -p^2 + m^{2} \right) \, e^{- i p (x - x')} = \] \[ = \delta(x - x') = \] \[ = N \int d^{4}p \, e^{- i p (x - x')} \] wobei wir im letzten Schritt die bekannte Fourierdarstellung der vierdimensionalen Delta-Funktion verwendet haben (siehe Wikipedia: Delta-Distribution). Da die Fouriertransformierte eindeutig ist, muss demnach für die Integranden gelten: \[ \left( -p^2 + m^{2} \right) \, \tilde{G}(p) = 1 \] Man könnte nun formal einfach
| \[ \tilde{G}(p) = - \frac{1}{p^{2} - m^{2}} \] |
schreiben, wenn wir mögliche Probleme bei \( p^{2} = m^{2} \) ignorieren.
Das geht beispielsweise für virtuelle Teilchen, wenn \( p^{2} \lt m^{2} \) ist.
Der obige Term ist dann genau (bis auf das irrelevante Vorzeichen)
die Impulsamplitude für die Propagation von Elementarwellen, und das ist auch die
Bedeutung der inneren Linien in Feynmangraphen. Die Herkunft dieses Terms
für innere Linien wäre damit geklärt.
Es lohnt sich jedoch, noch etwas genauer hinzusehen:
statischer Fall (Yukawa-Potential):
Betrachten wir zunächst den statischen Fall, bei dem die Ladungsverteilung \(j(x)\) und auch die Lösung \(\phi(x)\) nicht von der Zeit \(t\) abhängen. Die Zeitableitungen fallen hier weg und es ergibt sich aus der Differentialgleichung \( (-\hat{P}^{2} + m^{2}) \, \phi(x) = j(x) \) die Gleichung \[ \left ( \frac{d^2}{d\boldsymbol{x}^{2}} + m^{2} \right) \, \phi(\boldsymbol{x}) = j(\boldsymbol{x}) \] Für eine Punktladung ist das Yukawa-Potential eine Lösung dieser Differentialgleichung (siehe auch unten). Im masselosen Fall \(m=0\) entspricht diese Gleichung der Poisson-Gleichung für das statische elektrische Potential einer Ladungsverteilung, so dass für eine Punktladung das Coulomb-Potential als Lösung herauskommt.
Da die Zeitableitungen fehlen, lautet der Propagator hier \[ \tilde{G}(0,\boldsymbol{p}) = \frac{1}{\boldsymbol{p}^{2} + m^{2}} \] Es erfolgt also keine Energieübetragung zwischen Ladungsverteilung und Feld, sondern nur ein Impulsübertrag, ähnlich wie bei einem elastischen Stoß an einer massiven Wand. Hier gibt es (zumindest bei positiver Masse \(m\)) keine Probleme mit irgendwelchen Polen und wir können die Fouriertransformation für den statischen Fall ausrechnen: \[ G(x - x') = \] \[ = N \int d^{4}p \, \tilde{G}(0,\boldsymbol{p}) \, e^{- i p (x - x')} = \] \[ = N \int d^{3}p \, \frac{1}{\boldsymbol{p}^{2} + m^{2}} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')} \, \int dE \, e^{- i E (t - t')} = \] \[ = \frac{1}{(2 \pi )^{3}} \, \int d^{3}p \, \frac{1}{\boldsymbol{p}^{2} + m^{2}} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')} \, \delta(t - t') = \] \[ = \frac{1}{4 \pi} \, \frac{ e^{- m \, |\boldsymbol{x} - \boldsymbol{x}'|} }{ |\boldsymbol{x} - \boldsymbol{x}'| } \, \delta(t - t') \] Die etwas längliche Berechnung des Impulsintegrals beim letzten Gleichheitszeichen haben wir übersprungen – man muss hier im Impulsraum Kugelkoordinaten einführen und kann dann die Winkelintegration und die Impulsbetrags-Integration einzeln ausrechnen. Eingesetzt in die Gleichung \[ \phi(x) = \varphi(x) + \int d^{4}x' \, G(x - x') \, j(x') \] ergibt sich dann \[ \phi(t,\boldsymbol{x}) = \varphi(t,\boldsymbol{x}) \, + \] \[ + \int d^{4}x' \, \frac{1}{4 \pi} \, \frac{ e^{- m \, |\boldsymbol{x} - \boldsymbol{x}'|} }{ |\boldsymbol{x} - \boldsymbol{x}'| } \, \delta(t - t') \, j(t',\boldsymbol{x}') \] Das Zeitintegral über \(dx^0 = dt'\) können wir mit der Deltafunktion leicht ausführen. Außerdem lassen wir die Lösung \( \varphi(t,\boldsymbol{x}) \) der freien Wellengleichung weg, denn wir interessieren uns ja nur für statische Lösungen: \[ \phi(t,\boldsymbol{x}) = \int d^{3}x' \, \frac{1}{4 \pi} \, \frac{ e^{- m \, |\boldsymbol{x} - \boldsymbol{x}'|} }{ |\boldsymbol{x} - \boldsymbol{x}'| } \, j(t,\boldsymbol{x}') \] Auch dieser Ausdruck macht nur für statische Lösungen Sinn, denn er impliziert eine instantane Reaktion von \(\phi\) auf die Ladung \(j\). Genau das passiert also, wenn wir im Propagator \(E = 0\) setzen: physikalische Einflusse wirken dann ohne jede Zeitverzögerung, was nur im statischen Fall sinnvoll ist, da es dann keine Rolle spielt. Wir lassen also \(t\) weg und schreiben für die statische Lösung endgültig: \[ \phi(\boldsymbol{x}) = \int d^{3}x' \, \frac{1}{4 \pi} \, \frac{ e^{- m \, |\boldsymbol{x} - \boldsymbol{x}'|} }{ |\boldsymbol{x} - \boldsymbol{x}'| } \, j(\boldsymbol{x}') \] Wenn wir hier für die Ladungsverteilung eine Punktladung im Ursprung wählen, also \( j(\boldsymbol{x}') = q \, \delta(\boldsymbol{x}') \) setzen, so ergibt sich das Yukawa-Potential
| Yukawa-Potential: \[ \phi(\boldsymbol{x}) = \frac{q}{4 \pi} \, \frac{e^{- m |\boldsymbol{x}|} }{ |\boldsymbol{x}| } \] |
Für den masselosen Fall \(m = 0\) geht das Yukawa-Potential dabei in das Coulomb-Potential über.
Damit haben wir den Zusammenhang zwischen Teilchenmasse \( m \)
und der Reichweite eines statischen Potentials \( \phi(\boldsymbol{x}) \)
hergeleitet.
Startpunkt war dabei eine klassische Diffentialgleichung für \(\phi\), die sowohl ebene Wellen als auch statische Lösungen zulässt (analog zu den Gleichungen für die elektromagnetischen Potentiale).
Die ebenen Wellen können wir in der Quantenmechanik mit Teilchen in Verbindung bringen, welche die Masse \(m\) aufweisen und für die \( p^{2} = m^{2} \) gilt. Entsprechend haben wir oben den Wellenzahl-Vierervektor \(p\) teilweise direkt als Viererimpuls und den Parameter \(m\) als Teilchenmasse interpretiert, was nur über die Verbindung zur Quantenmechanik Sinn macht.
Wir haben die Wellenbeschreibung dann erweitert und Elementarwellen (Propagatoren) eingeführt, die durch eine aufblitzende Punktladung erzeugt werden. Mit Hilfe dieser Elementarwellen können wir jede Lösung der Diffentialgleichung durch Überlagerung zusammenbauen.
In Analogie zu den ebenen Wellen wollen wir die Elementarwellen ebenfalls als Teilchenamplituden interpretieren, wobei diesmal allerdings nicht \( p^{2} = m^{2} \) gilt, sondern die zugehörige Impulsamplitude die Form \[ \tilde{G}(p) = - \frac{1}{p^{2} - m^{2}} \] hat. Daher sprechen wir hier auch von virtuellen Teilchen. Virtuelle Teilchen sind nicht direkt messbar, genauso wie Elementarwellen nicht direkt messbar sind. Erst ihre summierte Wirkung (das Integral) ergibt einen messbaren Effekt. Im statischen Fall ergibt diese summierte Wirkung gerade das Yukawa-Potential, wobei die virtuellen Teilchen (Elementarwellen) hier keine Energie übertragen, sondern nur Impuls.
allgemeiner Fall (Feynman-Propagator):
(nur der Vollständigkeit halber für daran interessierte Leser)
Im allgemeinen dynamischen Fall müssen wir uns die Pole bei bei \( p^{2} = m^{2} \) im Propagator \[ \tilde{G}(p) = - \frac{1}{p^{2} - m^{2}} \] genauer ansehen, wenn wir das Fourier-Integral für \( G(x - x') \) ausführen wollen. Letztlich läuft es darauf hinaus, dass wir kausale zeitliche Randbedingungen formulieren müssen, um dem Fourierintegral eine definierte Bedeutung zu geben.
Im vorherigen Kapitel 5.1 hatten wir in den Zusatzinfos die Feynman-Stückelberg-Interpretation für negative Energien kennengelernt, die letztlich eine Forderung ist und für die Stabilität des Vakuums sorgt. Die Kernaussage lautet:
|
Feynman-Stückelberg-Interpretation:
|
Um konsistent mit dieser Interpretation bzw. Forderung zu sein,
geht man im Energie-Fourierintegral für \(G(x - x')\) so vor:
Man fasst die Energie \(E\) als komplexe Variable auf, verschiebt die beiden Energie-Pole in \( \tilde{G}(p) \) um einen winzigen positiven reellen Betrag \(\epsilon\) entlang der imaginären Achse nach oben bzw. unten und wertet dann das Energie-Integral dann mit Hilfe des Residuensatzes für \(\epsilon\) gegen Null aus. Wichtig ist dabei, dass durch das infinitesimale Verschieben der Pole je nach Vorzeichen von \( t - t' \) der richtige Energiepol relevant wird.
Der folgende Ansatz (Feynman-Propagator genannt) funktioniert, wie wir gleich sehen werden:
| Feynman-Propagator im Impulsraum: \[ \tilde{G}(p) = - \frac{1}{p^{2} - m^{2} + i \epsilon} \] |
Den Nenner schreiben wir etwas um, um die Polstruktur in der Energie besser zu sehen,
wobei wir die Abkürzung
\[
E_{p} := + \sqrt{\boldsymbol{p}^{2} + m^{2}}
\]
verwenden und quadratische Terme in \(\epsilon\) (das ja gleich noch gegen Null gehen soll) vernachlässigen:
\[
p^{2} - m^{2} + i \epsilon = \]
\[ =
E^{2} - \boldsymbol{p}^{2} - m^{2} + i \epsilon =
\]
\[ =
E^{2} - E_{p}^{2} + i \epsilon =
\]
\[ =
E^{2} - \left( E_{p} - i \frac{\epsilon}{2E_{p}} \right)^{2} =
\]
\[ =
[E + (E_{p} - i \epsilon')] \cdot
[E - (E_{p} - i \epsilon')]
\]
mit der winzigen positiven reellen Zahl
\[
\epsilon' := \frac{\epsilon}{2E_{p}}
\]
Es gibt also in der komplexen E-Ebene zwei Pole bei
\[
\pm (E_{p} - i \epsilon')
\]
Da wir \(E\) als komplexe Variable auffassen, können die \(E\)-Integration im Fourierintegral
\[
G(x - x') = N \int d^{4}p \, \tilde{G}(p) \, e^{- i p (x - x')}
\]
mit Hilfe des Residuensatzes ausführen. Dazu brauchen wir einen geschlossenen Weg in der komplexen \(E\)-Ebene.
Im Integrationsweg nehmen wir daher zu der Integration über reelle \(E\)
noch eine Integration über einen (unendlich groß werdenden)
Halbkreis hinzu, der den Integrationsweg schließt.
Den Halbkreis legen wir je nach dem Wert von \( t - t' \) so, dass der Imaginärteil von \(E\) auf diesem Halbkreis in \( e^{- i E (t - t')} \) einen exponentiellen Abfall bewirkt und der Halbkreis keinen Beitrag zum Integral liefert.
Für positives \( t - t' \) muss der Imaginärteil \(\mathrm{Im}(E)\) auf dem Halbkreis also negativ sein, so dass \[ e^{- i \, (i \, \mathrm{Im}(E) \, (t - t')} = e^{\mathrm{Im}(E) (t - t')} \] mit wachsendem negativen \( \mathrm{Im}(E) \) exponentiell abfällt. In diesem Fall legen wir den Halbkreis also unter die reelle \(E\)-Achse. Bei negativem \( t - t' \) machen wir es genau umgekehrt.

Die Pole des Feynman-Propagators in der komplexen \(E\)-Ebene.
Der rote Integrationsweg (ins Unendliche ausgedehnt) wird für den Fall \(t \gt t'\) verwendet.
Im anderen Fall \(t' \gt t\) muss man den Integrationsweg in der oberen Halbebene schließen.
Der Residuensatz sagt nun in diesem speziellen Fall
(siehe Wikipedia: Residuensatz):
\[
\int_{\gamma} dE \, \frac{f(E)}{E-a} = \pm 2 \pi \, i \, f(a)
\]
wobei \(\gamma\) ein einfach geschlossener Weg in der komplexen \(E\)-Ebene ist, der den Pol \(a\)
einmal umrundet, wobei das Vorzeichen rechts aussagt, ob der Weg entgegen oder im Uhrzeigersinn um den Pol \(a\)
herumgeht. Die Funktion \(f(E)\) muss dabei im Bereich des Weges und auch im davon umschlossenen Gebiet
holomorph sein, also eine komplexe Ableitung besitzen und ohne Pole sein (zum Begriff der komplexen
Ableitung siehe auch Die Grenzen der Berechenbarkeit, Kapitel 5.2).
Für positives \( t - t' \) hatten wir den Weg unten herum geschlossen, so dass der Weg im Uhrzeigersinn den Pol \( + (E_{p} - i \epsilon') \) umschließt. Es gilt daher nach dem Residuensatz für \(\epsilon'\) gegen Null \[ G(x - x') \, \theta(t - t') = \] \[ = \theta(t - t') \, N \int d^{4}p \, \tilde{G}(p) \, e^{- i p (x - x')} = \] \[ = \theta(t - t') \, N \int dE \, d^{3}p \] \[ \frac{- \, e^{- i E (t - t')} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')}} { [E + (E_{p} - i \epsilon')] \, [E - (E_{p} - i \epsilon')] ] } = \] \[ = \theta(t - t') \, 2 \pi \, i \, N \int \frac{d^{3}p}{2E_{p}} \, e^{- i E_{p} (t - t')} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')} \] wobei das Minuszeichen aufgrund des Umlaufsinns des Weges weggefallen ist. Konsistent mit der Feynman-Stücklberg-Interpretation wurde also für positives \( t - t' \) der Pol bei \( + E_{p} \) herausgegriffen.
Für negatives \( t - t' \) hatten wir den Weg oben herum geschlossen, so dass der Weg gegen den Uhrzeigersinn den Pol \( - (E_{p} - i \epsilon') \) umschließt. Also erhalten wir für \( \epsilon' \) gegen Null \[ G(x - x') \, \theta(t' - t) = \] \[ = \theta(t' - t) \, N \int d^{4}p \, \tilde{G}(p) \, e^{- i p (x - x')} = \] \[ = \theta(t' - t) \, N \int dE \, d^{3}p \] \[ \frac{- e^{- i E (t - t')} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')}} { [E + (E_{p} - i \epsilon')] \, [E - (E_{p} - i \epsilon')] } = \] \[ = \theta(t' - t) \, 2 \pi \, i \, N \int \frac{d^{3}p}{2E_{p}} \, e^{+ i E_{p} (t - t')} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')} \] Diesmal ist das Vorzeichen aufgrund des negativen Nenners in \( (- 1) / [-2 E_{p}] \) weggefallen. Konsistent mit der Feynman-Stücklberg-Interpretation wurde also für negatives \( t - t' \) (Wellen, die in die Vergangenheit reisen) der Pol bei der negantiven Energie \( - E_{p} \) herausgegriffen.
Zusammengefasst ergeben beide Terme für beliebiges \( t - t' \)
| Feynman-Propagator (Raum-Zeit-Abhängigkeit): \[ G(x - x') = \] \[ = \frac{i}{(2 \pi )^{3}} \int \frac{d^{3}p}{2E_{p}} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')} \] \[ \left[ \theta(t - t') \, e^{- i E_{p} (t - t')} + \theta(t' - t) \, e^{+ i E_{p} (t - t')} \right] = \] \[ = \frac{i}{(2 \pi )^{3}} \int \frac{d^{3}p}{2E_{p}} \, e^{- i E_{p} |t - t'|} \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')} \] |
Dabei ist \( \frac{d^{3}p}{2E_{p}} \) das relativistische (d.h. Poincaré-invariante)
Integrationsmaß im Impulsraum
(siehe Die Symmetrie der Naturgesetze, Kapitel 4.10).
Für \(t \gt t'\) haben wir es also mit dem Term \[ e^{- i E_{p} (t - t')} \] zu tun, also mit einer Teilchen-Welle positiver Energie, die sich vorwärts in der Zeit von \(t'\) nach \(t\) bewegt, und für \(t' \gt t\) gilt der Term \[ e^{+ i E_{p} (t - t')} = e^{- i (- E_{p}) (t - t')} = e^{- i E_{p} (t' - t)} \] also eine Welle negativer Energie, die sich rückwärts in der Zeit von \(t'\) nach \(t\) bewegt und die gleichbedeutend ist mit einer Antiteilchen-Welle positiver Energie, die sich vorwärts in der Zeit von \(t\) nach \(t'\) bewegt. Je nachdem, wie \(t\) und \(t'\) zueinander liegen, beschreibt \( G(x - x') \) also die Ausbreitung einer Teilchen- oder Antiteilchen-Welle vom kleineren Zeitpunkt zum größeren Zeitpunkt hin.
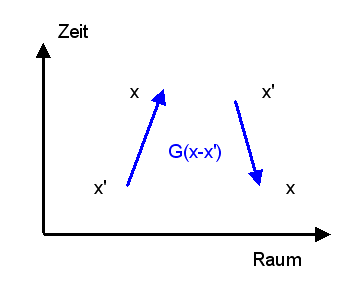
Im Feynmangraph stellt man \( G(x - x') \) meist durch eine Pfeil von \(x'\) nach \(x\) dar (siehe das Bild unten). Wenn \(t \gt t'\) ist, so zeigt dieser Pfeil in die positive Zeitrichtung und kann als Teilchen-Amplitude mit positiver Energie interpretiert werden. Ist dagegen \(t' \gt t\) so zeigt der Pfeil in die negative Zeitrichtung und kann entweder als formale Teilchenamplitude mit negativer Energie interpretiert werden, die in negativer Zeitrichtung läuft, oder als Antiteilchenamplitude mit positiver Energie, die in positiver Zeitrichtung läuft. Das verdeutlicht die Bedeutung der Pfeilrichtung in den Feynmangraphen.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 21 January 2024