
Quelle: Wikimedia Commons File:Dirac.gif,
Copyright abgelaufen.
Zusammenfassung des Buchkapitels:
Die Quarks im Inneren der Hadronen haben mittlere Geschwindigkeiten von der Größenordnung der Lichtgeschwindigkeit. Das ist eine Folge der extrem starken Kräfte, die die Quarks auf sehr kleinem Raum zusammenketten. Für die Quarkstruktur der Hadronen muss man also neben Quanteneffekten auch die spezielle Relativitätstheorie berücksichtigen.
Eine Quantentheorie, die die spezielle Relativitätstheorie berücksichtigt, nennt man eine relativistische Quantenfeldtheorie. Die nichtrelativistische Schrödingergleichung muss dazu in einem ersten Schritt durch andere relativistische Gleichungen ersetzt werden. Die zwei prominentesten Vertreter sind die Klein-Gordon-Gleichung für Teilchen mit Spin Null und die Diracgleichung für Fermionen (siehe Zusatzinfos unten).

Quelle:
Wikimedia Commons File:Dirac.gif,
Copyright abgelaufen.
Betrachten wir als Beispiel die Diracgleichung, die für Fermionen (also Spin 1/2) gilt.
Sie liefert die korrekte Beziehung zwischen relativistischer Gesamtenergie \(E\)
und Impuls \(p\):
\[
E^{2} = (mc^{2})^{2} + (pc)^{2}
\]
Was sie nicht liefert, ist die Zusatzbedingung, dass \(E\) positiv sein muss, denn
auch negative Energien erfüllen die obige Gleichung,
was physikalisch sinnlos ist.
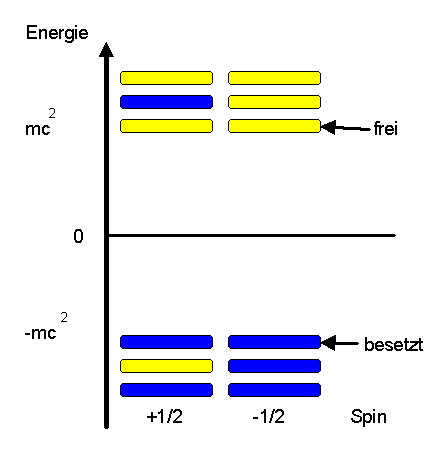
Paul Dirac kam nun auf folgende Idee: Der niedrigste Energiezustand ist derjenige, bei dem alle negativen Energiezustände bereits besetzt sind (sie können nach dem Pauliprinzip ja nur mit je einem Fermion besetzt werden). Also identifizieren wir diesen Gesamtzustand mit dem physikalischen Vakuum, der aus physikalischer Sicht ebenfalls der Zustand mit der niedrigsten möglichen Energie ist.
Was geschieht nun, wenn man einen einzigen negativen Energiezustand nicht besetzt? Der See aus Fermionen mit negativer Energie würde gleichsam ein Loch bekommen. Dieses Loch kann man als Antiteilchen interpretieren. Bei Elektronen wäre ein solches Elektronen-Loch ein Anti-Elektron, auch Positron genannt. Das Positron trägt dabei eine positve Elementarladung, da durch das Loch ja eine negative Elementarladung fehlt.
Man kann durch Energiezufuhr auch ein Elektron aus einem negativen Energieniveau in ein positives Energieniveau anheben. Das würde physikalisch bedeuten, dass sich allein durch Zufuhr von Energie aus dem Vakuum ein Elektron und ein Positron hervorzaubern lassen, die sich umgekehrt auch wieder unter Abgabe von Energie gegenseitig vernichten können, was dem Zurückfallen des Elektrons in sein negatives Energieniveau entsprechen würde.
Das von Dirac vorhergesagte Positron wurde tatsächlich im
Jahre 1932 von Anderson in der kosmischen Höhenstrahlung entdeckt.
Auch zu jedem weiteren Teilchen ist seitdem
ein entsprechendes Antiteilchen gefunden worden.
Streng genommen ist die Idee des Diracsees aus heutiger Sicht etwas überholt, und bei Bosonen funktioniert sie auch nicht, da hier das Pauliprinzip nicht gilt. Eine Alternative bietet die Feynman-Stückelberg-Interpretation, die unten in den Zusatzinfos dargestellt wird.
Nach Steven Weinberg folgt die Existenz von Antiteilchen aus dem Zusammenspiel von Quantentheorie und spezieller Relativitätstheorie (Lorentz-Invarianz) sowie der Tatsache, dass weit voneinander entfernte Vorgänge sich gegenseitig nicht kausal beeinflussen (Cluster Decomposition Principle). Mehr dazu siehe Die Symmetrie der Naturgesetze, Kapitel 4.15 Aufbau der Quantenfeldtheorie nach Steven Weinberg. In jeder Quantenfeldtheorie erzwingt also das Zusammenspiel von spezieller Relativitätstheorie und Quantentheorie die Existenz von Antiteilchen.
Es ist nicht einfach, in einer Quantenfeldtheorie die Wechselwirkung zwischen Teilchen korrekt zu beschreiben. Wenn diese Wechselwirkung nicht allzu stark ist, dann kann man die sogenannte Störungsrechnung anwenden und die Wechselwirkung schrittweise immer genauer in die Rechnung mit einbeziehen. Dabei geht man analog zur Reihenentwicklung in der Mathematik vor, wie man sie beispielsweise von der Formel \[ R = \frac{1}{1 - q} \] kennt: Für kleine \(q\) kann man \(R\) als geometrische Reihe schreiben \[ R = 1 + q + q^{2} + q^{3} + q^{4} + \, ... \] und näherungsweise dann nur einige wenige Summanden berücksichtigen, da diese schnell immer kleiner werden. Das Ergebnis dieser Störungsrechnung werden die Feynmangraphen sein, die wir im nächsten Kapitel kennenlernen werden.
In einer relativistischen Quantenfeldtheorie kann Energie in Teilchen umgewandelt werden und umgekehrt. Aus der Energie-Zeit-Unschärferelation \[ \Delta E \cdot \Delta t \gt \frac{\hbar}{2} \] (siehe Kapitel 2.5) folgt, dass für sehr kurze Zeiten die Energie eines Teilchens die Beziehung \[ E^{2} = (mc^{2})^{2} + (pc)^{2} \] verletzen darf, und zwar umso mehr, je kürzer die Zeitspanne ist. Man kann sich vorstellen, dass dadurch für kurze Zeiten im Vakuum virtuelle Teilchen-Antiteilchenpaare entstehen und auch wieder vergehen. Das Vakuum ist also in diesem Sinn keineswegs leer, sondern eine wabernde Suppe aus virtuellen Teilchen, die ständig entstehen und vergehen. Diese wabernde Suppe hat reale physikalische Auswirkungen. Ein Beispiel ist der Casimir-Effekt, der besagt, dass zwischen zwei dicht benachbarten metallischen Platten im Vakuum eine winzige anziehende Kraft wirkt.
Der Einfluss virtueller Teilchen ist bei allen physikalischen Vorgängen in der Quantenfeldtheorie präsent. So ist ein frei durch den Raum fliegendes Elektron ständig von einer fluktuierenden Wolke aus virtuellen Teilchen-Antiteilchen-Paaren umgeben. Dabei werden die positiv geladenen virtuellen Positronen vom negativ geladenen Elektron angezogen, während die negativ geladenen virtuellen Elektronen abgestoßen werden. Man sagt, das Vakuum wird durch die Anwesenheit des Elektrons polarisiert. Ein physikalisches Elektron ist daher immer mit einer virtuellen Teilchenwolke umgeben, die seine physikalischen Eigenschaften wie Masse und elektrisches Feld mitbestimmt.
Die relativistische Quantenfeldtheorie erlaubt die Beschreibung
physikalischer Phänomene mit einer bisher unübertroffenen Präzision.
So lässt sich der Einfluss der Polarisationswolke auf das
gut messbare magnetische Moment des Elektrons (beschrieben durch den
sogenannten g-Faktor) sehr genau berechnen.
Hier der Vergleich zwischen Messung und Berechung:
| Berechnung: | \( g_e = 2,002 \, 319 \, 304 \, 363 \, 22(46) \) |
| Messung: | \( g_e = 2,002 \, 319 \, 304 \, 362 \, 56(35) \) |
(siehe z.B. Wikipedia: Landé-Faktor). In Klammern ist dabei jeweils die Unsicherheit in den letzten Dezimalstellen angegeben. Besser geht es kaum!
Man kann auch beim Myon den g-Faktor sehr genau berechnen und experimentell bestimmen. Dabei reagiert der Myon-g-Faktor sehr viel empfindlicher auf schwere virtuelle Teilchen als der Elektron-g-Faktor. Der experimentell ermittelte Myon-g-Faktor beträgt \[ g_\mu = 2,002 \, 331 \, 841 \, 10(48) \] der im Rahmen des Standardmodells berechnete Myon-g-Faktor beträgt \[ g_\mu = 2,002 \, 331 \, 836 \, 20(86) \] d.h. es gibt anscheinend eine kleine Abweichung, die oft als Hinweis auf eine Physik jenseits des Standardmodells gedeutet wird.
Es stellt sich heraus, dass der Begriff Ort eines Teilchens in der Quantenfeldtheorie nur noch sehr beschränkt einen Sinn ergibt. Die Ortsunschärfe ist in der Quantenfeldtheorie durch die Beziehung \[ \Delta x \gt \frac{\hbar}{E} \] gegeben, wobei für ruhende massive Teilchen die relativistische Energie \(E\) durch \(E = mc^{2}\) gegeben ist.
Im Buchkapitel finden Sie eine Tabelle mit einigen typischen Ortsunschärfen. Die Ursache für die Ortsunschärfe liegt darin, dass man für eine sehr genaue Ortsmessung sehr viel Energie auf kleinem Raum konzentrieren muss, was zur Bildung störender Teilchen-Antiteilchen-Paaren führt. Deshalb findet man in der Quantenfeldtheorie auch keine Wellenfunktionen mit dem Ort als Messgröße (für den Impuls funktioniert es dagegen). Mehr zum Ort in der Quantenfeldtheorie finden Sie unten in den Zusatzinfos.
Welche Größen sind im Prinzip gleichzeitig messbar? Es sind die Impulse und Spinkomponenten der freien Teilchen vor und nach einer Teilchenkollision oder dem Teilchenzerfall! Diese Größen können wir analog zu einer Wellenfunktion in einer Quanten-Tabelle eintragen und im Rahmen der relativistischen Quantenfeldtheorie die entsprechenden Wahrscheinlichkeitspfeile berechnen. Man bezeichnet eine solche Tabelle auch als Streumatrix (S-Matrix).
In der Quantenfeldtheorie werden auch Wechselwirkungen und Kraftfelder durch Teilchen (Feldquanten) beschrieben. Licht besteht, wie wir wissen, aus einzelnen Photonen, sobald man genauer hinschaut! Aber auch alle anderen elektromagnetischen Felder werden in der Quantenfeldtheorie durch Photonen beschrieben.
Allgemein findet man, dass die Beschreibung einer Wechselwirkung durch Kraftfelder dann nicht mehr ausreicht, wenn diese Felder sehr schwach werden oder sehr schnell veränderlich sind. Die Feldbeschreibung wird dann durch eine Beschreibung mit reellen und virtuellen Feldquanten (also Teilchen) ersetzt. Von der Beschreibung durch Teilchen kann man wieder zu einer Beschreibung durch Kraftfelder zurückkehren, wenn sehr viele nicht zu energiereiche Feldquanten kohärent an einem betrachteten physikalischen Prozess beteiligt sind.
Die starke Wechselwirkung zwischen den Quarks in einem Hadron kann nicht mehr gut durch ein klassisches Kraftfeld beschrieben werden. Sie muss durch virtuelle Feldquanten beschrieben werden, die man Gluonen nennt.
Anders als Photonen, die auch als freie Teilchen existieren, gibt es Gluonen nur innerhalb der Hadronen. Ein Gluon transportiert nämlich starke Farbladungen zwischen den Quarks hin und her und ist deshalb kein weißes Teilchen (ein Photon transportiert dagegen keine elektrische Ladung – es ist elektrisch neutral). Nach dem Prinzip des Confinement können aber nur weiße Objekte als freie Teilchen existieren. Da Gluonen Farbladungen tragen, können sie auch direkt miteinander wechselwirken, anders als Photonen.
When you combine quantum mechanics with relativity you increase its [i.e. quantum mechanics] logical fragility. You find that unless you arrange the theory in just the right way you get nonsense, like effects preceding causes, or infinite probabilities.
(Steven Weinberg: A Designer Universe?)
a) Klein-Gordon-Gleichung
b) Diracgleichung
c) Negative Energien und Antiteilchen (Feynman-Stückelberg-Interpretation)
d) Über den Aufenthaltsort eines freien spinlosen Teilchens in der relativistischen Quantenfeldtheorie
e) Felder und Feldquanten
f) Relativistische Ortsunschärfe und Comptonwellenlänge
Weitere Informationen zum g-Faktor und dem magnetischen Dipolmoment des Elektrons und Myons
gibt es in den Zusatzinfos zu Kapitel 2.8.
Für Fortgeschrittene:
Einige Grundlagen der relativistischen Quantenfeldtheorie habe ich in
Die Symmetrie der Naturgesetze, Kapitel 4: Die Quantentheorie
sowie im Webbuch
Quantenfeldtheorie und Eichfelder dargestellt.
Am Besten hat nach meiner Meinung Steven Weinberg
den konsistenten Aufbau der Quantenfeldtheorie in seinem Buch
The Quantum Theory of Fields (Vol. 1) beschrieben.
Eine Übersicht der wesentlichen Schritte habe ich in
Die Symmetrie der Naturgesetze, Kapitel
4.15 Aufbau der Quantenfeldtheorie nach Steven Weinberg zusammengestellt.
In Kapitel 2.3 hatten wir eine Motivation für die nichtrelativistische Schrödingergleichung gegeben. Ganz analog kann man auch die Klein-Gordon-Gleichung motivieren:
Wie bei der Schrödingergleichung in Kapitel 2.3 gehen wir wieder von der Energie-Impuls-Beziehung und der ebenen Welle aus. Die ebene Welle ist auch relativistisch gegeben durch \[ \psi(t,\boldsymbol{x}) = e^{- \frac{i}{\hbar} \, (E t - \boldsymbol{p x})} \] (wobei \(E\) hier die relativistische Gesamtenergie ist und \(\boldsymbol{p}\) der Impuls) und es gelten daher wieder die Gleichungen \[ i \hbar \, \frac{d}{dt} \, \psi(t,\boldsymbol{x}) = E \, \psi(t,\boldsymbol{x}) \] \[ \frac{\hbar}{i} \, \frac{d}{d\boldsymbol{x}} \, \psi(t,\boldsymbol{x}) = \boldsymbol{p} \, \psi(t,\boldsymbol{x}) \] Was sich im Vergleich zur nichtrelativistischen Theorie ändert, ist die Beziehung zwischen Energie \(E\) und Impuls \(\boldsymbol{p}\). Diese ist in der relativistischen Theorie gegeben durch \[ E^{2} = (mc^{2})^{2} + (\boldsymbol{p} c)^{2} \] Damit diese Gleichung erfüllt ist, muss für die ebene Welle die Gleichung
| \[ \left(i \hbar \, \frac{d}{dt}\right)^{2} \, \psi(t,\boldsymbol{x}) = \] \[ = \left[ (mc^{2})^{2} + c^{2} \left( \frac{\hbar}{i} \, \frac{d}{d\boldsymbol{x}} \right)^{2} \right] \, \psi(t,\boldsymbol{x}) \] |
gelten. Das ist die Klein-Gordon-Gleichung. Die ebene Welle oben ist eine Lösung dieser Gleichung, und jede andere Lösung lässt sich aus ebenen Wellen zusammensetzen.
Die Klein-Gordon-Gleichung ist eine relativistische Verallgemeinerung der Schrödingergleichung für freie Teilchen, d.h. hier gibt es keinen Wechselwirkungsterm wie beispielsweise ein Potential. Natürlich kann man noch Potentiale in die Gleichung einfügen, aber das würde hier zu weit führen.
Es ist praktisch, auf die übliche Schreibweise mit Vierervektoren überzugehen (siehe Zusatzinfos zu Kapitel 3.2). Wir fassen also die Zeit \(t\) (mal Lichtgeschwindigkeit \(c\)) und die drei Raumkoodinaten \(\boldsymbol{x}\) zu einem Vierervektor \(x\) zusammen: \[ x = \begin{pmatrix} ct \\ \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} \] mit \(x^0 = ct\) (die Indizes schreiben wir hier oben).
Analog fassen wir die relativistische Gesamtenergie \(E\) und den räumlichen Impuls \(\boldsymbol{p}\) zum Viererimpuls p zusammen (\(p\) nicht verwechseln mit dem oben benutzten Betrag des räumplichen Impulses \(|\boldsymbol{p}|\), den wir ebenfalls \(p\) genannt haben): \[ p = \begin{pmatrix} p^0 \\ \boldsymbol{p} \end{pmatrix} = \begin{pmatrix} E/c \\ \boldsymbol{p} \end{pmatrix} \] Wechselt man das Bezugssystem, d.h. die Raumzeitkoordinaten werden mit der Lorentzmatrix \(\Lambda\) umgerechnet: \[ x' = \Lambda \, x \] so wird auch \(p\) entsprechend umgerechnet: \[ p' = \Lambda \, p \] d.h. sowohl \(x\) als auch \(p\) sind Vierervektoren. Die Minkowski-Metrik \(g(u,w)\) zweier Vierervektoren \(u\) und \(w\) ändert sich dabei nicht, d.h. es gilt \[ g(u,w) = g(\Lambda u, \Lambda w) \] mit \[ g(u,w) := u^{0} w^{0} - \boldsymbol{u w} = \] \[ = u^{0} w^{0} - (u^{1} w^{1} + u^{2} w^{2} + u^{3} w^{3}) \] Die Energie-Impuls-Beziehung \[ E^{2} = (mc^{2})^{2} + (\boldsymbol{p}c)^{2} \] können wir damit etwas umschreiben: \[ (E/c)^{2} - \boldsymbol{p}^{2} = (mc)^{2} \] Links steht die Minkowski-Metrik \(g(p,p)\), d.h. die Energie-Impuls-Beziehung lautet in dieser Schreibweise einfach \[ g(p,p) = (mc)^{2} \] Oft schreibt man auch \(p^{2}\) statt \(g(p,p)\) und \(p x \) statt \(g(p,x)\), was wir hier vermeiden, um keine Verwechselungen zu produzieren.
In der Vierervektor-Schreibweise sieht auch die ebene Welle ganz einfach aus: \[ \psi(x) = e^{- \frac{i}{\hbar} \, g(p,x)} \] Wir wollen noch einen Ableitungs-Vierervektor \( D \) definieren, und zwar so, dass \[ i \hbar \, D \, \psi(t,\boldsymbol{x}) = p \, \psi(t,\boldsymbol{x}) \] ist. Das sind vier Gleichungen, nämlich \[ i \hbar \, D^{\mu} \, \psi(t,\boldsymbol{x}) = p^{\mu} \, \psi(t,\boldsymbol{x}) \] mit \( p = (E/c, \boldsymbol{p}) \) und dem Raumzeit-Index \(\mu = 0, 1, 2, 3\).
Vergleichen wir das mit den obigen Gleichungen, so sehen wir, dass \[ D = \begin{pmatrix} \frac{1}{c} \frac{d}{dt} \\ - \frac{d}{d\boldsymbol{x}} \end{pmatrix} \] sein muss.
Auch für \(D\) können wir die Minkowski-Metrik bilden: \[ g(D,D) = \frac{1}{c^2} \frac{d^2}{dt^2} - \frac{d^2}{d\boldsymbol{x}^2} \] wobei \[ \frac{d^2}{d\boldsymbol{x}^2} = \frac{d^2}{(dx^1)^2} + \frac{d^2}{(dx^2)^2} + \frac{d^2}{(dx^3)^2} \] der Laplace-Operator ist. Die Klein-Gordon-Gleichung lautet dann \[ (i \hbar)^{2} \, g(D,D) \, \psi(x) = (mc)^{2} \, \psi(x) \] Manchmal bildet man aus \(D\) auch den Viererimpulsoperator \[ \hat{P} := i \hbar D \] so dass einfach \[ \hat{P} \, \psi(t,\boldsymbol{x}) = p \, \psi(t,\boldsymbol{x}) \] ist. Die Klein-Gordon-Gleichung lautet dann sehr intuitiv \[ g(\hat{P},\hat{P}) \, \psi(x) = (mc)^{2} \, \psi(x) \] passend zu der Energie-Impuls-Beziehung \( g(p,p) = (mc)^{2} \).
Oft wird die Klein-Gordon-Gleichung auch in Komponentenschreibweise mit Hilfe der Einsteinschen Summenkonvention geschrieben (Summation über doppelte Indices sowie Hoch- und Herunterziehen der Indices mit Hilfe der metrischen Matrix (siehe Zusatzinfos zu Kapitel 3.2). Dabei verwendet man die Raum-Zeit-Ableitungen \[ \partial_{\mu} := \frac{\partial}{\partial x^{\mu}} \] und \[ D^{\mu} = \partial^{\mu} = g^{\mu\nu} \, \partial_{\mu} \] (mit Summe über den doppelten Index \(\nu\) inbegriffen). Die Klein-Gordon-Gleichung lautet dann \[ (i \hbar)^{2} \, \partial_{\mu} \partial^{\mu} \, \psi(x) = (mc)^{2} \, \psi(x) \] In natürlichen Einheiten (in denen man \(\hbar\) und \(c\) in den Formeln weglassen kann) wird daraus einfach
| \[ (\partial_{\mu} \partial^{\mu} + m^{2}) \, \psi(x) = 0 \] |
Bei der Schrödingergleichung kann man \( \psi(t,\boldsymbol{x}) \) direkt als Wahrscheinlichkeitsamplitude für den Teilchenort interpretieren. Das ist bei der Klein-Gordon-Gleichung nicht der Fall!
Außerdem gibt es neben Lösungen zu positiver Energie auch Lösungen mit negativer Energie. Wie man diese Probleme angehen kann, finden Sie in Die Symmetrie der Naturgesetze, Kapitel 4.12: Spin 0 und die Klein-Gordon-Gleichung (nur für Fortgeschrittene!).
Insgesamt kann man sagen: Bei der Klein-Gordon-Gleichung ist \( \psi(x) \) keine Wellenfunktion, sondern ein relativistisches Feld, und man muss die Verbindung zu den Quantenzuständen (Wellenfunktionen) und dem Skalarprodukt (Wahrscheinlichkeitsamplituden) erst noch herstellen. Dabei findet man, dass die entsprechenden Quantenzustände Spin Null aufweisen und dass negative Energien etwas mit Antiteilchen zu tun haben.
Historisch war es so, dass man aufgrund dieser Probleme nach einer anderen Gleichung suchte, die ebenfalls die korrekte relativistische Energie-Impuls-Beziehung ergibt und die zugleich einige dieser Probleme nicht aufweist. So kam man auf die Diracgleichung.
Man vermutete, dass einige Probleme der Klein-Gordon-Gleichung daher kamen, dass in ihr die zweite Ableitung nach der Zeit auftrat. In der Schrödingergleichung tritt dagegen nur die erste Ableitung nach der Zeit auf. Also suchte man nach einer relativistischen Gleichung, die auch nur die erste Ableitung nach der Zeit enthält.
Nun hängt die Zeitableitung aber bei der ebenen Welle mit der Energie zusammen, und die tritt nun einmal quadratisch in der relativistischen Energie-Impuls-Beziehung \( E^{2} = (mc^{2})^{2} + (pc)^{2} \) auf.
Nun kann man natürlich die Wurzel ziehen: \[ E = \sqrt{(mc^{2})^{2} + (pc)^{2}} \] Nur wie macht man daraus eine Wellengleichung? Einfach analog die Wurzel in der Klein-Gordon-Gleichung zu ziehen ergibt keine sinnvolle Gleichung, die beispielsweise ebene Wellen erlaubt. Wie zieht man also sinnvoll die Wurzel in der Klein-Gordon-Gleichung?
Paul Dirac kam im Jahr 1928 auf folgende Idee: Er zog gleichsam die Wurzel aus der Klein-Gordon-Gleichung \[ g(\hat{P},\hat{P}) \, \psi(x) = (mc)^{2} \, \psi(x) \] indem er folgenden Ansatz machte: \[ \gamma(\hat{P}) \, \psi(x) = mc \, \psi(x) \] mit dem Viererimpulsoperator \[ \hat{P} := i \hbar D = i \hbar \, \begin{pmatrix} \frac{1}{c} \frac{d}{dt} \\ - \frac{d}{d\boldsymbol{x}} \end{pmatrix} \] wobei wie oben bei ebenen Wellen \[ \hat{P} \, \psi(t,\boldsymbol{x}) = p \, \psi(t,\boldsymbol{x}) \] sein soll. Und das ist sie auch schon: die berühmte Diracgleichung \( \gamma(\hat{P}) \, \psi(x) = mc \, \psi(x) \).
Nur was ist dabei \( \gamma(\hat{P}) \)?
Es soll analog zu \( \hat{P} \) ein linearer Operator sein, den man auf \(\psi(x)\) anwenden kann. Um zur Energie-Impuls-Beziehung vorzudringen, kann man \( \gamma(\hat{P}) \) ein zweites mal auf die Diracgleichung \( \gamma(\hat{P}) \, \psi(x) = mc \, \psi(x) \) anwenden: \[ \gamma(\hat{P}) \, \gamma(\hat{P}) \, \psi(x) = mc \, \gamma(\hat{P}) \, \psi(x) \] Rechts kann man \( \gamma(\hat{P}) \, \psi(x) \) nach der Diracgleichung durch \( mc \, \psi(x) \) ersetzen und erhält: \[ \gamma(\hat{P}) \, \gamma(\hat{P}) \, \psi(x) = (mc)^{2} \, \psi(x) \] Wenn man nun \[ \gamma(\hat{P}) \, \gamma(\hat{P}) = g(\hat{P},\hat{P}) \] fordert, so erhält man daraus wieder die Klein-Gordon-Gleichung und damit die relativistische Energie-Impuls-Beziehung. Man wird also die Klein-Gordon-Gleichung nicht wirklich los, aber man hat zusätzlich die Diracgleichung erhalten, die nur die erste zeitliche Ableitung enthält.
Was für ein Objekt ist also \(\gamma(\hat{P})\)?
Wir wollen es etwas allgemeiner angehen und jedem Vierervektor \(u\) (und damit auch dem Vierer-Impulsoperator \(\hat{P}\)) ein solches Objekt \(\gamma(u)\) zuordnen, so dass \[ \gamma(u) \, \gamma(w) = g(u,w) \] ist. Dabei soll \(\gamma(u)\) linear von \(u\) abhängen, d.h. \[ \gamma(u + w) = \gamma(u) + \gamma(w) \] \[ \gamma(\lambda u) = \lambda \, \gamma(u) \] für komplexe Zahlen \(\lambda\).
Offenbar muss man dafür \(\gamma(u)\) und \(\gamma(w)\) addieren und mit komplexen Zahlen multiplizieren können (d.h. sie bilden einen Vektorraum), und man muss sie auch miteinander multiplizieren können, d.h. sie bilden eine sogenannte Algebra.
Wegen der Zusatzbedingung \( \gamma(u) \, \gamma(w) = g(u,w) \) spricht man von einer Clifford-Algebra. Mehr dazu finden Sie in Die Symmetrie der Naturgesetze, Kapitel 4.11: Clifford-Algebren und Spingruppen.
Konkret kann man \(\gamma(u)\) durch eine komplexwertige 4-mal-4-Matrix darstellen. Da \(\gamma(u)\) linear in \(u\) sein soll, kann man vier Basismatrizen \( \gamma_{\mu} \) (mit \(\mu\) von 0 bis 3) einführen und \[ \gamma(u) = \sum_{\mu} \gamma_{\mu} \, u^{\mu} = \] \[ = \gamma_{0} \, u^{0} + \gamma_{1} \, u^{1} + \gamma_{2} \, u^{2} + \, \gamma_{3} u^{3} \] schreiben (analog für den Operator \(\gamma(\hat{P})\)).
Die Bedingung \( \gamma(u) \, \gamma(w) = g(u,w) \) führt dann auf die Bedingung \[ \gamma_{\mu} \, \gamma_{\mu} = g_{\mu\nu} \] mit der metrischen Diagonalmatrix \[ g = (g_{\mu\nu}) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \] Die vier Basismatrizen \( \gamma_{\mu} \) nennt man auch Diracmatrizen. Es gibt mehrere Möglichkeiten, solche Matrizen konkret aufzustellen.
Damit können wir die Diracgleichung auch explizit ausschreiben: \[ \frac{1}{c} \gamma_{0} \, i \hbar \frac{d}{dt} \, \psi(x) + \sum_{k=1}^{3} \, \gamma_{k} \, \frac{\hbar}{i} \frac{\partial}{\partial x^{k}} \, \psi(x) = \] \[ = mc \, \psi(x) \] Die Diracgleichung ist dann eine Matrix-Differentialgleichung (denn die \(\gamma_{\mu}\) sind komplexwertige 4-mal-4-Matrizen) und \(\psi(x)\) besitzt entsprechend vier komplexe Komponenten.
Die obige Matrixgleichung können wir mit Hilfe der Einsteinschen Summenkonvention auch schreiben als \[ i \hbar \gamma_{\mu} \partial^{\mu} \psi(x) = mc \, \psi(x) \] Meist bringt man mit Hilfe der metrischen Matrix noch die Indices nach oben bzw. unten, wobei \( \gamma_{\mu} \partial^{\mu} = \gamma^{\mu} \partial_{\mu} \) ist: \[ i \hbar \gamma^{\mu} \partial_{\mu} \psi(x) = mc \, \psi(x) \] In natürlichen Einheiten können wir \(\hbar\) und \(c\) wieder weglassen und haben:
| \[ (i \gamma^{\mu} \partial_{\mu} - m) \, \psi(x) = 0 \] |
Die folgende ebene Welle ist eine Lösung der Diracgleichung: \[ \psi(x) = u(p) \, e^{- \frac{i}{\hbar} \, g(p,x)} \] Dabei tritt noch der Vorfaktor \(u(p)\) auf. Setzt man diese ebene Welle in die Diracgleichung \( \gamma(\hat{P}) \, \psi(x) = mc \, \psi(x) \) ein, so ist \[ \gamma(\hat{P}) \, \psi(x) = \gamma(p) \, \psi(x) \] und es folgt \[ \gamma(p) \, u(p) = mc \, u(p) \] d.h. \(u(p)\) hat analog zu \(\psi(x)\) vier Komponenten und ist Lösung dieser Matrixgleichung.
Wie bei der Klein-Gordon-Gleichung ist auch bei der Diracgleichung \(\psi(x)\) ein relativistisches Feld. Man spricht auch vom Dirac-Spinor. Wieder muss man die Verbindung von \(\psi(x)\) zu den Quantenzuständen (Wellenfunktionen) und dem Skalarprodukt (Wahrscheinlichkeitsamplituden) erst noch herstellen und auch die Lösungen mit negativer Energie entsprechend zuordnen. Dabei stellt man fest, dass die entsprechenden Quantenzustände zu Spin 1/2 gehören, also zu Fermionen, und dass Lösungen mit negativer Energie mit Antiteilchen zusammenhängen.
Es wird dabei auch deutlich, warum \(u(p)\) vier Komponenten hat:
Die Wellenfunktion hat zunächst nur zwei Komponenten (je eine für die Spinkomponente + 1/2 und - 1/2), aber es lassen sich daraus zwei verschiedene Felder bilden: ein rechtshändiges und ein linkshändiges Feld.
Diese Felder werden uns bei der schwachen Wechselwirkung wieder begegnen, denn die W-Bosonen wirken nur auf linkshändige Fermionfelder. Rechts- und linkshändiges Feld unterscheiden sich in ihrem Verhalten bei Boosts (Geschwindigkeitstransformationen), denn einmal wird die positive und einmal die negative Helizität verstärkt.
Da aber rechts- und linkshändiges Feld aus derselben Wellenfunktion gebildet werden, müssen sie miteinander zusammenhängen. Genau diesen Zusammenhang stellt die Diracgleichung her. Mehr dazu in Die Symmetrie der Naturgesetze, Kapitel 4.13: Spin 1/2, Dirac- und Weyl-Gleichung sowie Kapitel 4.13 b: Spin 1/2, Helizität versus Chiralität.
Im Buchkapitel (siehe oben) hatten wir das Problem negativer Energien angesprochen und sind auf die Lösung dieses Problems durch den Dirac-See eingegangen, bei dem alle negativen Energiezustände besetzt sind. Löcher in diesem See entsprechen dann Antiteilchen.
Leider weist dieser Lösungsversuch einige Probleme auf. Er funktioniert insbesondere nicht bei Bosonen, da bei diesen Teilchen das Pauli-Prinzip nicht gilt und negative Energiezustände daher mit beliebig vielen Teilchen besetzt werden können, ohne jemals voll zu sein.
Es gibt jedoch eine andere Lösungsmöglichkeit, die auf Feynman und Stückelberg zurückgeht und die wir hier kurz plausibel machen wollen (siehe dazu auch mein Buch Feynman und die Physik, Kap. 3.2: Das Meisterstück: Feynman-Diagramme und Antiteilchen).
Zur Vereinfachung der Schreibweise verwenden wir dabei natürliche Einheiten (siehe Kapitel 3.3), d.h. wir messen Energien, Impulse, Zeiten und Abstände in Energieeinheiten und lassen deshalb die Umrechungsfaktoren \(\hbar\) und \(c\) weg. Außerdem schreiben wir \[ p x := g(p,x) = E t - \boldsymbol{p x} \] Die Klein-Gordon-Gleichung (und ebenso die Dirac-Gleichung) besitzen als Lösungen ebene Wellen der Form \[ e^{- i px} \] (impulsabhängige Vorfaktoren lassen wir vereinfacht weg). Dabei ergibt sich aus der Klein-Gordon-Gleichung oder Diracgleichung die Bedingung \[ p^{2} = E^{2} - \boldsymbol{p}^{2} = m^{2} \] (mit \(p^2 := g(p,p)\), siehe oben). Freigestellt nach \(E\) bedeutet das: \[ E =\pm \sqrt{m^{2} + \boldsymbol{p}^{2}} \] d.h. die Energie \(E\) in der ebenen Welle kann sowohl positive als auch negative Werte aufweisen.
Bei positiver Energie \(E\) haben wir kein Problem, denn wir können ebene Wellen \[ e^{- i px} = e^{- i \, (E t - \boldsymbol{p x})} \] mit positiver Energie \(E\) problemlos mit Teilchen in Verbindung bringen, die sich mit Impuls \(\boldsymbol{p}\) von kleineren zu größeren Zeiten \(t\) hin kausal bewegen.
Negative Energien \(E\) sind für ebene Wellen zunächst auch kein Problem, denn das bedeutet nur, dass sich bei negativer Energie die Wellenamplitude an jedem Ort mit wachsender Zeit \(t\) genau umgekehrt dreht wie bei positiver Energie.
Das Problem entsteht erst dann, wenn wir dieses negative \(E\) direkt mit einer Teilchenenergie identifizieren, denn es können nun im Vakuum unter Energieabgabe beliebig viele Teilchen negativer Energie entstehen und das Vakuum wäre instabil.
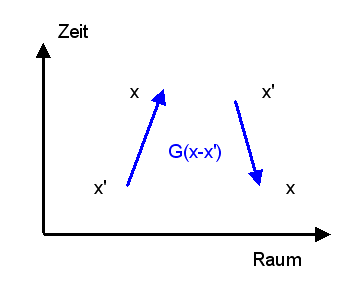
Bei negativem \(E\) müssen wir also \( -E \) als Teilchenenergie auffassen, oder genauer: als Antiteilchen-Energie. Wegen \[ e^{- i E (-t)} = e^{- i (-E) t} \] entspricht eine Welle, die sich mit negativer Energie E rückwärts in der Zeit (also mit \(-t\) bei wachsendem \(t\)) ausbreitet, einer Welle mit positiver Energie \(-E\), die sich vorwärts in der Zeit \(t\) ausbreitet. Wir verlangen daher, dass sich Wellen negativer Energie immer rückwärts in der Zeit ausbreiten müssen, Wellen positiver Energie dagegen vorwärts in der Zeit. Man spricht hier von der Feynman-Stückelberg-Interpretation:
|
Feynman-Stückelberg-Interpretation:
|
Warum identifiziert man negative Energien mit Antiteilchen?
Wenn eine Welle eine Ladung \(q\) von A nach B transportiert, so transportiert die
rückwärts in der Zeit laufende Welle die Ladung \(q\) von B nach A, was sich genauso auswirkt
wie der Transport der Gegenladung \(-q\) von A nach B.
Wellen negativer Energie transportieren dieselbe Ladung \(q\) wie Wellen positiver Energie
(da für die dieselbe Gleichung gilt), nur rückwärts in der Zeit, was sich wie der Transport
der Gegenladung \(-q\) vorwärts in der Zeit auswirkt. Daher ist es naheliegend, von Antiteilchen zu sprechen.
Formal sauber kann man die Feynman-Stückelberg-Interpretation mit Hilfe von Propagatoren (siehe Zusatzinfos zu Kapitel 5.2) oder mit Hilfe des Vielteilchen-Quantenformalismus darstellen. Die Idee dabei ist, dass man eine Welle mit positiver oder negativer Energie zu einem Zeitpunkt \(t'\) erzeugt und zu einem anderen Zeitpunkt \(t\) vernichtet und nun abhängig vom Energievorzeichen festlegt, wie die zeitliche Reihenfolge von \(t\) und \(t'\) aussieht.
Bei positiver Energie stellt man die Bedingung \(t \gt t'\), d.h. diese Welle wird erst erzeugt und später wieder vernichtet.
Bei negativer Energie stellt man dagegen die Bedingung \(t' \gt t\), d.h. die Welle wird zu einem späteren Zeitpunkt \(t'\) erzeugt und zu einem früheren Zeitpunkt \(t\) vernichtet – sie läuft formal rückwärts in der Zeit.
Das ist auch der Grund dafür, warum man in den Feynmangrafen Antiteilchen mit einem Pfeil kennzeichnet, der rückwärts in der Zeit gerichtet ist. Nach der Feynman-Stückelberg-Interpretation ist eine solche rückwärts in der Zeit laufende Teilchenwelle negativer Energie gleichwertig zu einer Antiteilchen-Welle positiver Energie, die zur Zeit \(t\) erzeugt und zur späteren Zeit \(t'\) wieder vernichtet wird. Im Diracsee-Bild könnte man auch analog sagen, die Welle negativer Energie wird zunächst zur Zeit \(t\) vernichtet (so dass ein Loch entsteht) und später zur Zeit \(t'\) wieder erzeugt (so dass das Loch verschwindet).
Die Feynman-Stückelberg-Interpretation löst das Problem der negativen Energien
in der Klein-Gordon-Gleichung und in der
Dirac-Gleichung, denn es können nun keine Wellen negativer Energie mehr erzeugt werden, die in die Zukunft laufen – solche
Wellen laufen immer in die Vergangenheit.
Daher bleibt das Vakuum stabil, ganz analog zum Diracsee.
Dabei kommt man ohne den Diracsee aus, der nur bei Fermionen funktioniert,
ist aber andererseits auch konsistent mit der Idee des Diracsees.
Ich gebe allerdings zu, dass ich mit Wellen, die sich rückwärts in der Zeit ausbreiten, anschaulich manchmal meine Probleme habe. Klarer wird mir die Situation immer dann, wenn ich mir den Diracsee dazu vorstelle, denn dann ist es auch kein Problem mehr, eine Welle negativer Energie zur Zeit t zu vernichten und sie erst zur späteren Zeit t' wieder zu erzeugen – es entsteht eben in der Zwischenzeit ein Loch im Diracsee. Außerdem ist die Antiteilchen-Natur direkt klar, denn ein Loch muss genau die entgegengesetzten Größen (Ladung, Impuls, Energie, ...) haben wie das dort fehlende Teilchen. Deshalb habe ich im Buch zur Veranschaulichung den Diracsee verwendet, auch wenn er aus heutiger Sicht streng genommen veraltet ist.
In der modernen Formulierung der Quantenfeldtheorie verzichtet man meist ganz auf die Diskussion negativer Energien und arbeitet direkt mit Teilchen- und Antiteilchen-Zuständen (bzw. entsprechenden Erzeugungsoperatoren), die immer positive Energie haben. Der Zusammenhang zwischen Teilchen und Antiteilchen ist dann allerdings anschaulich nicht immer ganz transparent. Daher sind sowohl der Diracsee als auch die Feynman-Stückelberg-Interpretation für die Anschauung weiterhin nützlich, und letztlich spiegeln sie sich auch in der modernen Formulierung der Quantenfeldtheorie wider.
(für Leser mit mathematisch-physikalischem Hintergrundwissen)
Im Buchkapitel habe ich erwähnt, dass der Ort eines Teilchens in der relativistischen Quantenfeldtheorie nur noch eine untergeordnete Rolle spielt, da er sich nicht mehr beliebig genau messen lässt: Man muss zur genauen Ortsmessung Wellen mit immer kürzerer Wellenlänge und immer mehr Energie verwenden, so dass diese Energie irgendwann zur Bildung neuer Teilchen-Antiteilchen-Paare führt und eine weitere Steigerung der Messgenauigkeit verhindert.
Ist es dennoch möglich, zumindest im Prinzip auch in der Quantenfeldtheorie eine Wahrscheinlichkeitsamplitude für den Teilchenort zu definieren, analog zur nichtrelativistischen Wellenfunktion? Das wollen wir uns hier anschauen. Dabei wollen wir uns auf freie Teilchen ohne Spin beschränken, da bei wechselwirkenden Teilchen sofort virtuelle Teilchen ins Spiel kommen, und da wir uns die technischen Komplikationen des Spins hier ersparen wollen.
Für den Teilchenimpuls ist die Definition einer Impuls-Wahrscheinlichkeitsamplitude problemlos möglich. Im Detail geht das so:
Wir beginnen mit einer impulsabhängigen komplexwertige Funktion \( \phi(p) \) mit dem Viererimpuls \[ p = \begin{pmatrix} p^0 \\ \boldsymbol{p} \end{pmatrix} = \begin{pmatrix} E \\ \boldsymbol{p} \end{pmatrix} \] die eine Lösung der Klein-Gordon-Gleichung im Impulsraum mit positiver Energie sein soll, so dass \[ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}} \] (in natürlichen Einheiten) gilt (siehe oben sowie Die Symmetrie der Naturgesetze, Kapitel 4.12: Spin 0 und die Klein-Gordon-Gleichung ). Letztlich hängt also \(p\) und damit \( \phi(p) \) nur vom räumlichen Impuls \( \boldsymbol{p} \) ab, da \(p^{0}\) ja damit bereits festgelegt ist.
Bei einer Drehung oder einem Boost (Geschwindigkeitstransformation) des Teilchen-Quantenzustandes mit der 4-mal-4-Lorentzmatrix \( \Lambda \) wird der dadurch veränderte Quantenzustand durch eine neue Funktion
| \[ \phi'(p') := \phi(p) \] mit \[ p' = \Lambda p \] |
beschrieben, d.h. die neue Funktion \( \phi' \) hat beim veränderten Impuls \( p' = \Lambda p \) denselben Wert wie die alte Funktion \( \phi \) beim ursprünglichen Impuls \(p\). Wir haben hier also anschaulich eine aktive Transformation vor uns, bei der gleichsam das Wellenpaket geboostet oder gedreht wird. Dieses Transformationsgesetz passt dazu, dass wenn die Funktion \(\phi\) eine Lösung der Klein-Gordon-Gleichung ist, dann auch die neue Funktion \(\phi'\) eine Lösung der Klein-Gordon-Gleichung sein soll. Übrigens kann man die obige Gleichung auch in der Form \[ \phi'(p) = \phi(\Lambda^{- 1}p) \] schreiben.
Wenn \( \phi(p) \) bereits eine Wahrscheinlichkeitsamplitude für den Teilchenimpuls wäre, so müsste \[ \int_{G} d^{3}p \, |\phi(p)|^{2} \] die Wahrscheinlichkeit dafür sein, dass der Impuls \(\boldsymbol{p}\) im Wertebereich \(G\) liegt, denn das Betragsquadrat der Amplitude soll ja die Wahrscheinlichkeit (hier genauer die Wahrscheinlichkeitsdichte) dafür angeben, dass der entsprechende Wert gemessen wird.
Bei einer Lorentztransformation, die aus den Impulsen \( p \) die Impulse \( p' = \Lambda p \) und aus \(\phi\) die Funktion \(\phi'\) macht, sollte die Wahrscheinlichkeit, den Impuls nun im Gebiet \( G' = \Lambda G \) zu finden, genauso groß sein wie die Wahrscheinlichkeit, den Impuls zuvor im Gebiet \( G \) zu finden: \[ \int_{G'} d^{3}p' \, |\phi'(p')|^{2} = \int_{G} d^{3}p \, |\phi(p)|^{2} \] Nun ist bereits \( \phi'(p') = \phi(p) \), d.h. wir bräuchten im Integral rechts nur noch über \( p' = \Lambda p \) die Integrationsvariable von \(p\) nach \(p'\) zu wechseln und wenn dabei \( d^{3}p' = d^{3}p \) gilt, so wäre die geforderte Gleichung erfüllt.
Das Problem ist nur: bei Drehungen gilt diese Beziehung für das Integrationsmaß noch, nicht aber bei Boosts (Geschwindigkeitstransformationen). Zur Probe führen wir einen Boost in z-Richtung durch, wie er durch die folgenden Formeln beschrieben wird (siehe z.B. Die Symmetrie der Naturgesetze, Kapitel 3.3 sowie Kapitel 4.10 ): \[ (p^{0})' = \gamma p^{0} + \gamma u p^{3} \] \[ (p^{3})' = \gamma u p^{0} + \gamma p^{3} \] (Raumzeit-Indices hochgestellt geschrieben) mit dem Betrag der räumlichen Boostgeschwindigkeit \( u = |\boldsymbol{u}| \) (also hier kein Vierervektor!) und \[ \gamma = \sqrt{\frac{1}{1 - u^{2}}} \] sowie \[ p^{0} = \sqrt{m^{2} + (p^{3})^{2}} \] \[ (p^{0})' = \sqrt{m^{2} + (p^{3})'^{ 2}} \] Dabei wählen wir unser Bezugssystem so, dass die Impulse \(p^{1}\) und \(p^{2}\) gleich Null sind – sie werden beim Boost in z-Richtung ohnehin nicht verändert und spielen daher keine Rolle.
Wie wirkt sich das nun auf das Integrationsmaß des Impulses p^{3} aus? Wegen der Beziehung \[ \frac{dp^{0}}{dp^{3}} = \frac{d}{dp^{3}} \sqrt{m^{2} + (p^{3})^{2}} = \] \[ = \frac{1}{2 \, \sqrt{m^{2} + (p^{3})^{2}}} \, 2 p^{3} = \frac{p^{3}}{p^{0}} \] gilt: \[ (dp^{3})' = \frac{(dp^{3})'}{dp^{3}} \, dp^{3} = \] \[ = \left( \gamma u \frac{dp^{0}}{dp^{3}} + \gamma \frac{dp^{3}}{dp^{3}} \right) \, dp^{3} = \] \[ = \left( \gamma u \frac{p^{3}}{p^{0}} + \gamma \right) \, dp^{3} = \] \[ = \frac{ \gamma u p^{3} + \gamma p^{0} }{p^{0}} \, dp^{3} = \] \[ = \frac{(p^{0})'}{p^{0}} \, dp^{3} \] Division durch \( (p^{0})' \) ergibt \[ \frac{(dp^{3})'}{(p^{0})'} = \frac{dp^{3}}{p^{0}} \] Da außerdem für einen Boost in z-Richtung (3-Richtung) \( (dp^{1})' = dp^{1} \) und \( (dp^{2})' = dp^{2} \) ist, gilt für das Volumen-Integrationsmaß \( d^{3}p = dp^{1} dp^{2} dp^{3} \) bei Lorentztransformationen (oder allgemeiner Poincaré-Transformationen, wenn man Raum-Zeit-Translationen hinzunimmt) die Beziehung \[ \frac{d^{3}p'}{(p^{0})'} = \frac{d^{3}p}{p^{0}} \] Das ist also das Poincaré-invariante (oder auch Lorentz-invariante oder relativistisch invariante) Integrationsmaß für Impulse. Halten wir fest:
| Poincaré-invariantes Integrationsmaß für die Integration über Impulse p:
\[ \frac{d^3p}{2p^0} \] mit \[ p^0 = \sqrt{m^2 + \boldsymbol{p}^2} \] (den Faktor 2 kann man auch weglassen; er ist manchmal jedoch recht nützlich, weshalb wir ihn hinzugefügt haben) |
Dieses Ergebnis kann man auch sehr schön aus dem Poincaré-invarianten Integrationsmaß
\[
d^{4}p \; \delta(p^2 - m^2) \, \theta(p^0) =
\]
\[
= dp^{0} \, dp^{1} \, dp^{2} \, dp^{3} \;
\delta(p^2 - m^2) \, \theta(p^0)
\]
herleiten, wobei in der \(\delta\)-Funktion das Viererimpulsquadrat
\(p^2 = (p^0)^2 - \boldsymbol{p}^2\) steht,
was zusammen mit der \(\Theta\)-Funktion dafür sorgt, dass bei der Integration die Bedingung
\( p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}} \)
eingehalten wird –
siehe dazu Die Symmetrie der Naturgesetze, Kapitel 4.10,
dort nach Poincaré-invariantes Integrationsmaß suchen.
Wir wissen also jetzt, dass die folgende Beziehung für die Impulsintegrale bei Lorentztransformationen \(p' = \Lambda p\) gültig ist: \[ \int_{G'} \frac{d^{3}p'}{2(p^0)'} \, |\phi'(p')|^{2} = \int_{G} \frac{d^{3}p}{2p^0} \, |\phi(p)|^{2} \] wenn für \(\phi(p)\) das einfache Transformationsgesetz \[ \phi'(p') = \phi(p) \] mit \( p' = \Lambda p \) gilt. Wir wollen also \[ \frac{\phi(p)}{\sqrt{2p^0}} \] mit \( p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}}\) als Wahrscheinlichkeitsamplitude für den Impuls interpretieren (Impuls-Wellenfunktion) in dem Sinn, dass dann
| Impuls-Wahrscheinlichkeit: \[ \int_{G} d^{3}p \, \left| \frac{\phi(p)}{\sqrt{2p^0}} \right|^{2} = \int_{G} \frac{d^{3}p}{2p^0} \, |\phi(p)|^{2} \] |
in jedem Bezugssystem die Wahrscheinlichkeit dafür angibt, dass der Impuls im Bereich \(G\) liegt.
Man muss also die ursprüngliche Funktion \(\phi(p)\), die das naheliegende Transformationsverhalten
\( \phi'(p') = \phi(p) \) besitzt,
noch mit dem Faktor \( 1 / \sqrt{2p^0} \)
normieren, so dass sie bezüglich des Maßes \( d^{3}p \)
in jedem Bezugssystem als Wahrscheinlichkeitsamplitude funktioniert.
Versuchen wir nun, auch bezogen auf den Ort eine passende Wahrscheinlichkeitsamplitude zu formulieren. Dazu bietet es sich an, in einem ersten Schritt die Lösung \(\phi(p)\) der Impulsraum-Klein-Gordon-Gleichung per Fouriertransformation in eine Lösung \(\psi(x)\) der üblichen Klein-Gordon-Differentialgleichung umzurechnen, wobei wir aber das Poincaré-invariante Maß im Impulsraum verwenden, um ein einfaches Lorentz-Transformationsverhalten sicherzustellen:
| \[ \psi(x) := N \, \int \frac{d^{3}p}{2p^0} \, \phi(p) \, e^{- i p x} \] mit \[ p^{0} = \sqrt{m^{2} + \boldsymbol{p}^{2}} \] \[ p x = g(p,x) = p^{0} x^{0} - \boldsymbol{p x} \] \[ N = (2 \pi)^{- 3/2} \] |
Für das Transformationsverhalten von \(\psi(x)\) rechnen wir mit \( x' := \Lambda x \)
und \( p' := \Lambda p \) sowie \( p' x' = p x \)
leicht nach:
\[
\psi'(x') :=
\]
\[
= N \,\int \frac{d^{3}p'}{2(p^0)'} \, \phi(p') \, e^{- i p' x'} =
\]
\[
= N \, \int \, \frac{d^{3}p}{2p^0} \, \phi(p) \, e^{- i p x} =
\]
\[
= \psi(x)
\]
also
| \[ \psi'(x') = \psi(x) \] mit \( x' = \Lambda x \). |
d.h. die neue Funktion \( \psi' \) hat am neuen Raumzeitpunkt \( x' = \Lambda x \)
denselben Wert wie die alte Funktion \( \psi \) beim ursprünglichen Raumzeitpunkt \(x\).
Das entspricht wieder der anschaulichen Vorstellung von einer aktiven Transformation, bei der man
beispielsweise das Objekt auf einen fahrenden Zug setzt.
Die Umkehrung der obigen Fouriertransformation lautet: \[ \frac{\phi(p)}{2p^0} = N \, \int d^{3}x \, \psi(x) \, e^{i p x} \] Um zu einer Orts-Wahrscheinlichkeitsamplitude zu gelangen, wollen wir das Impulsraum-Wahrscheinlichkeits-Integral \[ \int \frac{d^{3}p}{2p^0} \, |\phi(p)|^{2} \] durch \(\psi(x)\) ausdrücken, wobei wir über alle Impulse integrieren wollen: \[ \int \frac{d^{3}p}{2p^0} \, |\phi(p)|^{2} = \] \[ = \int d^{3}p \, 2p^0 \, \frac{\phi(p)^{*}}{2p^0} \, \frac{\phi(p)}{2p^0} = \] \[ = \int d^{3}p \, 2p^0 \] \[ N \, \int d^{3}y \, \psi(y)^{*} \, e^{- i p y} \] \[ N \, \int d^{3}x \, \psi(x) \, e^{i p x} = \] \[ = \int d^{3}y \, \int d^{3}x \, \psi(y)^{*} \, \psi(x) \] \[ N^{2} \, \int d^{3}p \,2p^0 \, e^{- i p (y - x)} \] Wäre der Faktor \( 2p^0 \) nicht da, so ergäbe das Impulsintegral im Wesentlichen einfach die Deltafunktion \( \delta^{3}(\boldsymbol{y} - \boldsymbol{x}) \) und für gleiche Zeiten \(x^{0} = y^{0}\) bekäme man als Ergebnis das Integral \[ \int d^{3}x \, |\psi(x)|^{2} \] heraus, in dem man \( \psi(x) \) als Wahrscheinlichkeitsamplitude für den Ort interpretieren könnte. Unser Ergebnis sieht aber anders aus: Es besteht aus einem Faltungsintegral \[ \int \frac{d^{3}p}{2p^0} \, |\phi(p)|^{2} = \] \[ = \int d^{3}y \, \int d^{3}x \, \psi(y)^{*} \, \psi(x) \, d(y - x) \] mit der Funktion \[ d(y - x) = N^{2} \, \int \, d^{3}p \, 2p^0 \, e^{- i p (y - x)} \] die wie eine Verschmierung zwischen den Raumzeitpunkten \(x\) und \(y\) wirkt, da der Faktor \( 2p^0 \) verhindert, dass eine Deltafunktion entsteht – es entsteht eine verschmierte Deltafunktion, also eine Art Glockenfunktion mit endlicher Breite. Diese Verschmierungsfunktion \( d(y - x) \) ist dabei nicht lorentzinvariant, denn auch die Integrationsmaße \(d^{3}y\) und \(d^{3}x\) sind nicht lorentzinvariant, das Gesamtintegral dagegen schon, da das ursprüngliche Impulsintegral lorentzinvariant ist.
Wir können das Feld \( \psi(x) \) also nicht direkt als Orts-Wahrscheinlichkeitsamplitude interpretieren, obwohl es anschaulich das passende Transformationsverhalten hätte. Es tritt eine Orts-Verschmierung auf, die durch die Funktion \( d(y - x) \) dargestellt wird.
Man könnte den Versuch machen, die Fouriertransformation vom Impulsraum zum Ortsraum etwas anders zu definieren, so dass der störende Faktor \( 2p^0 \) darin absorbiert wird:
| \[ \Psi(x) := N \, \int \, \frac{d^{3}p}{\sqrt{2p^0}} \, \phi(p) \, e^{- i p x} \] |
Hier steht im Nenner nur noch die Wurzel von \(2p^0\), so dass wir
\[
\int \frac{d^{3}p}{2p^0} \, |\phi(p)|^{2}
= \int d^{3}x \,
|\psi(x)|^{2}
\]
erhalten, d.h. man könnte \( \Psi(x) \) als Orts-Wahrscheinlichkeitsamplitude interpretieren.
Allerdings hat dieses \( \Psi(x) \) nun kein einfaches Transformationsverhalten mehr,
d.h. bei einem Boost
ist die neue Amplitude am geboosteten Punkt (ach ja, die Sprache ...)
nicht mehr einfach gleich der Amplitude am vorherigen Punkt,
sondern sie ergibt sich aus den Amplituden aus einem verschmierten
Bereich um den ursprünglichen Punkt herum, was die Interpretation
als Wahrscheinlichkeitsamplitude etwas trübt.
Das hängt auch damit zusammen, dass das Raumintegral \( \int d^{3}x \, ... \) für eine feste Zeit ausgewertet werden muss, also in der vierdimensionalen Raumzeit einen Unterraum gleichzeitiger Raumzeitpunkte erfasst. Nach einem Boost ist dieser Unterraum nicht mehr derselbe, da nun andere Ereignisse als gleichzeitig angesehen werden.
Wir können einen Zusammenhang zwischen dem Ortsamplituden-Kandidaten \( \Psi(x) \) und dem einfach transformierbaren Feld \( \psi(x) \) herstellen, wobei wir die Formel \[ \delta^{3}(\boldsymbol{p}' - \boldsymbol{p}) = N^{2} \int d^{3}x' \, e^{i (\boldsymbol{p}' - \boldsymbol{p}) \boldsymbol{x}'} \] verwenden und die Zeit gleich Null setzen: \[ \Psi(0, \boldsymbol{x}) = N \, \int \frac{d^{3}p}{\sqrt{2p^0}} \, \phi(p) \, e^{i \boldsymbol{p x}} = \] \[ = N \, \int \frac{d^{3}p}{2p^0} \, \int d^{3}p' \, \delta^{3}(\boldsymbol{p}' - \boldsymbol{p}) \, \sqrt{2(p^0)'} \, \phi(p) \, e^{i \boldsymbol{p x}} = \] \[ = N \, \int \frac{d^{3}p}{2p^0} \, \phi(p) \, \, \int d^{3}p' \] \[ N^{2} \int d^{3}x' \, e^{i (\boldsymbol{p}' - \boldsymbol{p}) \boldsymbol{x}'} \, \sqrt{2(p^0)'} \, e^{i \boldsymbol{p x}} = \] \[ = N^{3} \, \int d^{3}x' \, \int \frac{d^{3}p}{2p^0} \, \phi(p) \, e^{i \boldsymbol{p} (\boldsymbol{x} - \boldsymbol{x}')} \] \[ \int d^{3}p' \, e^{i \boldsymbol{p}' \boldsymbol{x}'} \, \sqrt{2(p^0)'} = \] \[ = N^{2} \, \int d^{3}x' \, \psi(0, \boldsymbol{x} - \boldsymbol{x}') \, \int d^{3}p' \, e^{i \boldsymbol{p}' \boldsymbol{x}'} \, \sqrt{2(p^0)'} = \] \[ = N \, \int d^{3}x' \, \psi(0, \boldsymbol{x} - \boldsymbol{x}') \, D(\boldsymbol{x}') \] mit der Verschmierungsfunktion \[ D(\boldsymbol{x}') := N \, \int d^{3}p' e^{i \boldsymbol{p}' \boldsymbol{x}'} \, \sqrt{2(p^0)'} \] die ähnlich zur Funktion \( d \) oben eine verschmierte Deltafunktion ist, analog zu einer Glockenkurve. Unser Ortsamplituden-Kandidat \( \Psi(x) \) entsteht also aus dem Feld \( \psi(x) \) über ein Faltungsintegral, das eine Verschmierung von \( \psi(x) \) bewirkt.
Fazit:
Das Klein-Gordon-Feld \( \psi(x) \) hat ein einfaches Transformationsverhalten, kann aber nicht direkt als Ortsamplitude interpretiert werden.
Über ein Faltungsintegral kann man daraus die Funktion \( \Psi(x) \) erzeugen, die man als Kandidaten für eine Ortsamplitude ansehen kann, die aber kein einfaches Transformationsverhalten mehr hat, was diese Interpretation einschränkt: Um die Aufenthaltswahrscheinlichkeit an einem Ort aus einem neuen Bezugssystem heraus zu beurteilen, braucht man die Aufenthaltswahrscheinlichkeiten des alten Bezugssystems aus einem ganzen Bereich um diesen Ort herum, was die Aufenthaltswahrscheinlichkeit zu einem verschmierten, nichtlokalen Phänomen macht.
Wäre ein Teilchen in einem Bezugssystem laut \( \Psi(x) \) scharf an einem bestimmten Ort lokalisiert, so wäre das in einem anderen Bezugssystem nicht der Fall. Letztlich steckt dahinter, dass man nie nur einen Punkt betrachten kann, sondern immer infinitesimale Raumbereiche \(d^{3}x\) betrachten muss, und \(d^{3}x\) ist nun einmal kein lorentzinvariantes Raummaß, da der Begriff der Gleichzeitigkeit vom Bezugssystem abhängt.
Zugegeben: das Thema ist nicht ganz einfach, aber zum Trost sei gesagt, dass sich bereits viele Physiker mit diesem Thema befasst haben, ohne je zu einer allgemein akzeptierten Definition für die Ortsamplitude durchgedrungen zu sein, was die damit verbundenen Schwierigkeiten verdeutlicht. Mehr dazu siehe z.B. Mir-Kasimov: Newton-Wigner postulates and commutativity of position operators.
Im Buch ist an vielen Stellen von Feldern und Feldquanten die Rede. So sind Photonen die Feldquanten des elektromagnetischen Feldes. Schauen wir uns etwas genauer an, wie Feldquanten und Felder zusammenhängen und wann man zu einer klassischen Beschreibung durch Felder übergehen kann.
Beim Übergang von Feldern zu Teilchen spielen ebene Wellen eine entscheidende Rolle. Jedes Feld kann man als Überlagerung ebener Wellen schreiben, und bei einer ebenen Welle können wir deren Frequenz und Wellenlänge wie gewohnt über das Planck'sche Wirkungsquantum in die Energie und den Impuls von Teilchen übersetzen – diese Teilchen sind dann die Feldquanten.
In einem klassischen Feld tragen die verschiedenen ebene Wellen mit unterschiedlichen Stärken (Fourieramplituden) zum Gesamtfeld bei. In der Quantenbeschreibung werden diese kontinuierlichen Amplituden ebener Wellen durch eine diskrete Anzahl (Besetzungszahl) an Feldquanten ersetzt, die den entsprechenden Wert für Energie und Impuls aufweisen, wie ihn die ebene Welle angibt. Aus den Fourieramplituden ebener Wellen werden also Besetzungszahlen für bestimmte Energie-Impuls-Werte. Man kann sich vorstellen, dass die in einer ebenen Welle enthaltene Energie dadurch quantisiert wird, da ja jedes Feldquant denselben Energiewert dazu beiträgt.
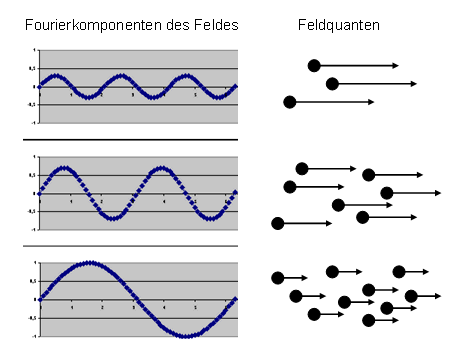
Diese Quantenzustände mit bestimmten Besetzungszahlen für die einzelnen Energie-Impuls-Werte
müssen für Bosonen symmetrisch und für Fermionen antisymmetrisch sein, so dass
man der Ununterscheidbarkeit identischer Teilchen Rechnung trägt
und das Pauli-Prinzip respektiert.
Diese Quantenzustände bilden nun eine
Basis für die insgesamt möglichen Quantenzustände, die eine beliebige quantenmechanische
Überlagerung der Basiszustände darstellen können (man denke an Wellenpakete und entsprechende Wellenfunktionstabellen)
– Quantenzustände können also sehr komplex werden.
Das klassische Feld wird in diesem Sinne durch quantenmechanische
Vielteilchenzustände ersetzt.
Wenn wir von einem freien Feld ohne Wechselwirkung mit irgendwelchen Ladungen oder Selbstwechselwirkungen ausgehen, also beispielsweise von einer elektromagnetischen Welle, dann sind die Feldquanten reelle, messbare Teilchen. Bei anderen Feldern (z.B. dem statischen elektrischen Feld einer Ladung) bekommt man es dagegen mit virtuellen Teilchen zu tun, die beispielsweise nur Impuls, aber keine Energie transportieren, da die Frequenzen der Fourierkomponenten Null sind, nicht aber die Wellenlängen (die Wellen sind also zeitlich eingefroren, schwingen also nur räumlich). Wir wollen im Folgenden im Zweifelsfall von einem freien Feld und reellen Feldquanten ausgehen.
In bestimmten Fällen kann man von der komplexen Beschreibung durch Feldquanten wieder zu der viel einfacheren Beschreibung durch klassische Felder zurückkehren. Wenn beispielsweise die Energie eines Feldquants sehr viel geringer ist als die insgesamt in der zugehörigen ebenen Welle enthaltene Feldenergie, dann spielt das einzelne Feldquant keine große Rolle mehr und der Einfluss der vielen Feldquanten summiert sich zu einer Gesamtwirkung analog der eines klassischen Feldes auf. Mit anderen Worten: Bei großen Besetzungszahlen für die einzelnen Energie-Impuls-Werte kann man zu einer klassischen Feldbeschreibung übergehen.
Bei energiearmen Feldquanten ist das meist kein Problem, aber was ist mit den hochfrequenten Feldanteilen, die zu hochenergetischen Feldquanten gehören? Hier muss die Zahl der Feldquanten zu hohen Frequenzen hin irgendwann klein werden, da ansonsten die Gesamtenergie aller Feldquanten immer weiter ansteigen würde, je höhere Frequenzen man hinzunimmt. In Landau-Lifschitz: Lehrbuch der theoretischen Physik, Band IV: Quantenelektrodynamik, Kap. I §5 findet man dazu die folgende Abschätzung:
Wenn man den Einfluss von Feldquanten auf ein Messergebnis sinnvoll durch ein klassisches Feld beschreiben will, so muss man ihren Einfluss über ein für den betrachteten Prozess typisches Zeitintervall \( \Delta t \) mitteln, in dem sich das klassische Feld nur wenig ändert.
Sehr hochenergetische Feldquanten gehören nun zu hochfrequenten Wellen, die in diesem Zeitintervall viele Schwingungen ausführen, so dass sich die einzelnen Schwingungen gegenseitig wegmitteln. Daher werden nur solche Frequenzen bei der Mittelung relevant bleiben, die nur zu wenigen Schwingungen im Zeitintervall \( \Delta t \) führen. Die Zahl der Schwingungen bei Frequenz \( f \) im Zeitintervall \( \Delta t \) ist gleich \( f \, \Delta t \). Diese Zahl soll in der Größenordnung von Eins oder weniger liegen. Meist multipliziert man noch mit \(2 \pi \) und schreibt \( \omega := 2 \pi f \) (Kreisfrequenz genannt). Die Bedingung lautet dann \[ \omega \, \Delta t \lt 1 \] oder gleichwertig \[ \omega_{max} = \frac{1}{\Delta t} \] (ist nur eine grobe Abschätzung – ein Faktor 10 ist da immer drin). Nur wenn die Feldquanten diese Bedingung erfüllen, werden sie bei der Mittelung über \( \Delta t \) nennenswert beitragen.
Damit haben wir eine Obergrenze für die Energie bzw. Frequenz der relevanten Feldquanten festgelegt. Nun müssen wir noch formulieren, dass wir bis zu dieser Obergrenze pro möglichem Teilchenimpuls (also pro Schwingungsmode) sehr viele Feldquanten brauchen, um bei dieser Schwingungsmode zu einem klassischen Feld übergehen zu können. Doch welche Teilchenimpulse sind möglich?
Um die Zahl der möglichen Teilchenimpulse quantifizieren zu können, betrachten wir ein würfelförmiges Raumvolumen \(V\) (das wir später beliebig groß machen können, da es bei unserer Betrachtung wieder wegfallen wird) und zählen die darin möglichen Frequenzen stehender Wellen (auch Moden genannt) bis zu dieser Energiegrenze. Dabei fordern wir, dass die Wellenamplituden an der Würfeloberfläche gleich Null werden, analog zu den Schwingungen einer eingespannten Gitarrensaite. Da man eine stehende Welle immer durch Überlagerung zweier gegenläufiger ebener Wellen gleicher Frequenz erzeugen kann, zählen wir mit den stehenden Wellen zugleich auch die möglichen ebenen Wellen (mal 2).
Quelle:
Wikimedia Commons File:Standing wave 2.gif, dort gemeinfrei
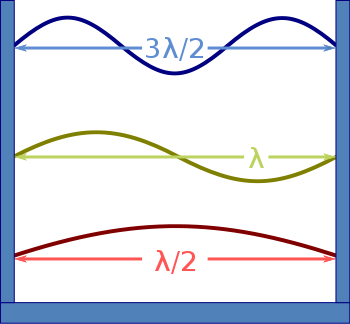
Quelle:
Wikimedia Commons File:Waves in Box.svg, Urheber: Wikipedia-User Badseed,
CC BY-SA 3.0 DEED
Die Wellenlänge \(\lambda\) einer stehenden Welle in einer Kantenrichtung
muss so sein, dass \(n\) halbe Wellenlängen \(\lambda/2\) die Kantenlänge \(L\) ergeben:
\[
n \, \frac{\lambda}{2} = L
\]
mit einer
beliebigen natürlichen Zahl \(n\).
Wir beschränken uns weiter auf masselose Feldquanten, beispielsweise Photonen,
für die
\[
c = \lambda f
\]
(\(c\) ist die Lichtgeschwindigkeit) gilt, so dass
\[
n = \frac{2 L}{\lambda} = \frac{2 L f}{c} = \frac{2 L \omega}{2 \pi c}
\]
ist.
Wir können nun die Zahl \(n\) der halben Wellenlängen auf der Strecke \(L\)
und die zugehörige Kreisfrequenz \(\omega\)
schrittweise bis zur oben festgelegten Obergrenze hochzählen, so dass das maximal mögliche
\( n_{max} \) nun zugleich die Zahl der auf der Strecke L
möglichen stehenden Wellen bis zur maximalen Kreisfrequenz
\( \omega_{max} = \frac{1}{\Delta t} \) ist:
\[
n_{max} = \frac{2 L \omega_{max}}{2 \pi c}
= \frac{L}{\pi c \, \Delta t}
\]
Da sich im Würfel stehende Wellen in allen drei Raumrichtungen ausbilden können, ist die
Gesamtzahl der stehenden Wellen bis zur Maximalfrequenz gleich \( n_{max}^{3} \).
Jede stehende Welle gehört dabei zu zwei möglichen Impulsen des Feldquants, so dass
\( (2 n_{max})^{3} \) auch die Anzahl der möglichen Feldquanten-Impulse \(n_{p}\)
im Volumen \( V = L^{3} \)
bis zur angegebenen Maximalfrequenz ist (verschiedene Spinrichtungen etc. vernachlässigen wir hier):
\[
n_p = (2 n_{max})^{3} = 8 \, \frac{L^3}{(\pi c \, \Delta t)^3}
\]
Da es sich nur um eine grobe Abschätzung handelt, lassen wir im Folgenden Zahlenfaktoren einfach weg
und schreiben für die Zahl \(n_{p}\) der im Volumen V möglichen Impulse:
\[
n_{p} = \frac{V}{(c \, \Delta t)^{3}}
\]
Wenn nun \( N \) die Gesamtanzahl der Feldquanten im Volumen \(V\) ist, so ist
\( N / n_{p} \) die durchschnittle Zahl der Feldquanten mit gleichem Impuls
(und daher auch mit derselben Energie). Diese Zahl soll groß sein, wenn wir zu einem klassischen Kraftfeld
übergehen wollen.
Nehmen wir konkret ein elektrische Feld \( \boldsymbol{E} \). Die im Volumen \(V\) enthaltene elektrische Feldenergie ist dann ungefähr gleich \[ \frac{\epsilon_{0}}{2} \, |\boldsymbol{E}|^{2} \, V \] (die magnetische Feldenergie lassen wir zur Vereinfachung weg). Die mittlere Photonenergie ist grob im Mittel ungefähr gleich der halben Maximalenergie, also ungefähr gleich \[ \frac{\hbar \, \omega_{max}}{2} = \frac{\hbar}{2 \, \Delta t} \] so dass die Zahl der Photonen \(N\) im Volumen \(V\) ungefähr durch \[ N = \frac{ \epsilon_{0} \, |\boldsymbol{E}|^{2} \, V}{\hbar \, \omega_{max}} \] (die Faktoren \(1/2\) im Zähler und Nenner kürzen sich weg) gegeben ist. Dividiert durch die Zahl der möglichen Photonimpulse \( n_{p} \) ergibt das \[ \frac{N}{n_{p}} = \frac{ \epsilon_{0} \, |\boldsymbol{E}|^{2} \, V}{\hbar \, \omega_{max}} \, \frac{(c \, \Delta t)^{3}}{V} = \] \[ = \frac{\epsilon_{0} \, |\boldsymbol{E}|^{2} \, \Delta t}{\hbar} \, (c \, \Delta t)^{3} = \] \[ = \frac{\epsilon_{0} \, |\boldsymbol{E}|^{2} \, (c \, \Delta t)^{4}}{\hbar c} \] Das ist also ungefähr die mittlere Zahl der Photonen mit gleichem Impuls, ausgedrückt durch die mittlere elektrische Feldstärke \(\boldsymbol{E}\), die gemittelt über das Zeitintervall \(\Delta t\) nennenswert beitragen (das Volumen \(V\) ist dabei herausgefallen).
Diese Zahl soll groß sein, wenn ein einzelnes Photon nicht ins Gewicht fallen soll, so dass man klassische Felder verwenden kann. Also muss \[ \frac{\epsilon_{0} \, |\boldsymbol{E}|^{2} \, (c \, \Delta t)^{4}}{\hbar c} \gg 1 \] sein, oder umgestellt:
| Bedingung für die Beschreibung durch ein klassisches elektrisches Feld: \[ \epsilon_{0} \, |\boldsymbol{E}|^{2} \gg \frac{\hbar c}{(c \, \Delta t)^{4}} \] |
wobei \( \gg \) für sehr viel größer als steht.
Das ist genau die Bedingung, die auch im Buchkapitel angesprochen wird: Das Feld muss hinreichend stark sein, und zwar umso stärker, je kürzer das Mittelungsintervall \(\Delta t\) ist. Dabei darf sich das Feld in diesem Zeitintervall nur wenig ändern.
Ist das Feld also zu schwach und dabei zu schnell veränderlich, so kann eine Feldbeschreibung nicht funktionieren und wir müssen zu einer Beschreibung durch Photonen übergehen (Beispiel: schwache radioaktive Gammastrahlung). Bei einer statischen Situation kann dagegen \( \Delta t \) sehr groß gemacht werden, so dass klassische Felder gut funktionieren. Ähnlich ist es bei (nicht zu schwachen) Radiowellen oder bei ausreichend starkem Licht.
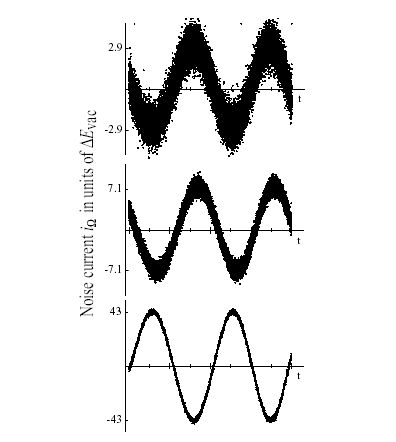
Bildquelle: measured quantum noise of three coherent states,
Wikimedia Commons File:Coherent noise compare3.jpg,
Credit: Gerd Breitenbach,
CC BY-SA 3.0 DEED
Bei Bosonen wie dem Photon ist der Übergang zu klassischen Feldern bei großen Besetzungszahlen
kein Problem, da sich Bosonen wegen der Symmetrie der Wellenfunktion
sehr gerne im selben Quantenzustand aufhalten.
Die Einteilchen-Wellenfunktion von Bosonen hat daher auch große Ähnlichkeit mit dem
entsprechenden klassischen Feld, denn man braucht ja (etwas vereinfacht) nur sehr viele Bosonen in dieselbe
Wellenfunktion zu pressen, so dass das klassische Feld entsteht.
Daher wundert es auch nicht, dass man manchmal beispielsweise das elektromagnetische Vektorpotential \( \boldsymbol{A} \) auch als Wellenfunktion des Photons bezeichnet, wobei allerdings \( \boldsymbol{A} \) nicht direkt eine Wahrscheinlichkeitsamplitude ist (d.h. man braucht noch eine Vorschrift (ein Skalarprodukt), um aus \( \boldsymbol{A} \) quantenmechanische Wahrscheinlichkeitsamplituden zu berechnen; siehe z.B. Feynman Vorlesung über Physik, Band III: Quantenmechanik, Kap. 21-4 oder Landau-Lifschitz: Lehrbuch der theoretischen Physik, Band IV: Quantenelektrodynamik, Kap. I §3).
Bei Fermionen wie beispielsweise dem Elektron ist das anders! Das Pauli-Prinzip bewirkt hier, dass jeder Quantenzustand (jeder Impulszustand bzw. jede Schwingungsmode) nur mit einem einzigen Fermion besetzt sein kann. Fermionen meiden sich gegenseitig. Zu jeder ebene Welle und damit jedem Energie-Impuls-Wert kann daher höchstens ein Fermion gehören (oder höchstens zwei, wenn man die beiden Spinwerte bei Spin 1/2 berücksichtigt).
Die entsprechenden Besetzungszahlen sind damit immer klein, so dass die Bedingung für ein klassisches Fermionfeld (große Besetzungszahlen für die relevanten Energie-Impuls-Werte) nie erfüllt sein können. Es gibt kein klassisches Fermionfeld!
Klassisch müsste man daher Fermionen durch Teilchenbahnen beschreiben, wobei aber die quantenmechanischen Eigenheiten des Spins unter den Tisch fallen, so dass aus einem Fermion einfach nur ein klassisches spinloses Teilchen wird – klassisch gibt es in diesem Sinne Fermionen also gar nicht, d.h. man benötigt zu ihrer Beschreibung zwingend die Quantentheorie.
Das merkt man beispielsweise auch sofort, wenn man versucht, viele identische Fermionen in einem immer kleineren Volumen zusammenzupressen. Das Pauli-Prinzip führt hier zu einem quantenmechanischen Gegendruck, der sich klassisch nicht erklären lässt. Genau dieser Druck ist es, der einen weißen Zwerg oder einen Neutronenstern vor dem endgültigen Gravitationskollaps bewahrt (bei einem weißen Zwerg sind es die Elektronen, bei einem Neutronenstern die Neutronen). Letztlich ist es auch dieser Gegendruck, der die Elektronenhülle der Atome stabilisiert und der der uns umgebenden Materie ihre Stabilität verleiht.
Eine scheinbare Ausnahme gibt es: Die Supraleitung. Die Leitungselektronen bilden dabei eine gemeinsame makroskopische Wellenfunktion, also so etwas wie ein klassisches komplexwertiges Feld – allerdings nicht als einzelne Fermionen, sondern in Form von Cooperpaaren, bei denen die beiden halbzahligen Fermionspins zusammen einen ganzzahligen Spin bilden (siehe Zusatzinfos zu Kapitel 6.1). Cooperpaare verhalten sich daher wie Bosonen, und es handelt sich letztlich um die makroskopische Wellenfunktion dieser bosonischen Cooperpaare, nicht aber um ein Fermionfeld.
Obwohl es kein klassisches Fermionfeld analog zum elektromagnetischen Feld geben kann, tut man im mathematischen Formalismus häufig zunächst so, als gäbe es eines. Ein Beispiel bilden die klassischen Feldgleichungen von Eichtheorien wie der QCD, die auf dem Prinzip der lokalen Eichinvarianz basieren – wie haben dieses Prinzip in Buchkapitel 5.3 kennengelernt. Es basiert in der üblichen Formulierung auf klassischen Fermionfeldern, in der QCD beispielsweise pro Farbladung (und pro Quarksorte) eines. Eine Eichtransformation kann nun diese Fermionfelder für verschiedene Farbladungen lokal unterschiedlich ineinander verdrehen und umwandeln, oder anders ausgedrückt: Sie kann lokal die Farbladungen beliebig umdefinieren.
In manchen Fällen ist diese Vorgehensweise unmittelbar einsichtig, beispielsweise beim Aharanov-Bohm-Effekt (siehe Zusatzinfos zu Kapitel 5.3), denn dort hat man es nicht mit einem klassischen Fermionfeld, sondern mit einer Ein-Fermion-Wellenfunktion zu tun, deren Phase man umändern darf.
Bei den klassischen Feldgleichungen von Eichtheorien ist diese Vorgehensweise dagegen zunächst suspekt, denn es gibt ja keine klassischen Fermionfelder, sondern nur quantenmechanische Fermion-Wellenfunktionen. Nun kann man eine Ein-Fermion-Wellenfunktionen generell in ein quantenmechanisches Feld (z.B. einen Dirac-Spinor \( \psi \)) umrechnen und umgekehrt, so wie man auch eine Ein-Photon-Wellenfunktion in das Photon-Vektorpotential \( \boldsymbol{A} \) umrechnen kann. In den Fällen, bei denen Teilchenerzeugung keine Rolle spielt, kann man daher das Fermionfeld direkt im Sinne einer Wellenfunktion interpretieren und so beispielsweise die Eigenschaften eines Elektrons im elektromagnetischen Feld mit Hilfe der Diracgleichung direkt berechnen (was beispielsweise den g-Faktor 2 ergibt, siehe Zusatzinfos zu Kapitel 2.8).
Wenn man dagegen ganz allgemein bei Eichtheorien mit klassischen Fermionfeldern hantiert, so verwendet man diese einfach als formales Hilfsmittel, damit man dieselben Methoden wie bei klassischen Bosonfeldern anwenden kann, um zu einer Quantenfeldtheorie zu gelangen. Die Symmetrieprinzipien (z.B. das Eichprinzip) wendet man dabei auf diese klassischen Felder an, so dass sie sich anschließend auf die daraus abgeleitete Quantentheorie übertragen. Physikalisch relevant ist für die Fermionen nur diese Quantentheorie, nicht aber das klassische Fermionfeld. Fermionen und die zugehörigen Felder können letztlich nur quantenmechanisch beschrieben werden. Spin 1/2 ist nun einmal ein reines Quantenphänomen. So wechseln Fermionfelder bei einer 360-Grad-Drehung das Vorzeichen, was für eine Wellenfunktion in Ordnung ist, nicht aber für ein klassisches Feld. Auch das Pauli-Prinzip ist ein reines (relativistisches) Quantenphänomen. Klassische Fermionfelder können also immer nur formale Hilfsmittel sein.
Wer den üblichen mathematischen Formalismus der Feldquantisierung kennt, der erinnert sich, dass dort aus Feldern formal Feldoperatoren werden. Man spricht auch von zweiter Quantisierung, was ein sehr verwirrender Ausdruck ist, denn man quantisiert Felder nur einmal, indem man zur Beschreibung durch Feldquanten übergeht. Der Begriff kommt daher, dass man beispielsweise Fermionfelder manchmal direkt mit Einteilchen-Wellenfunktionen in Beziehung setzen kann, was einer ersten Quantisierung entspricht. Der Übergang zu einer Vielteilchen-Quantentheorie wäre dann die zweite Quantisierung. Dennoch bleibt dieser Begriff problematisch, und Steven Weinberg plädiert beispielsweise dafür, ihn komplett zu streichen.
Die Feldoperatoren lassen sich als Linearkombinationen von Einteilchen-Erzeugungs- und Vernichtungs-Operatoren schreiben – nennen wir sie wie üblich \( a^{+} \) und \( a \) (Impuls- und Spin-Indices lassen wir vereinfacht weg). Dabei gilt für Bosonen bei geeigneter Normierung der Teilchenzustände die Vertauschungsrelation \[ a a^{+} - a^{+} a = \hbar \omega \] (für gleiche Impulse und Spins), was letztlich erst die Interpretation dieser Operatoren als Teilchenerzeuger und -vernichter ermöglicht. Beim Übergang zu klassischen Feldern kann man etwas vereinfacht formal \( \hbar \) gegen Null gehen lassen, so dass sich \( a \) und \( a^{+} \) wie gewöhnliche vertauschbare Zahlen verhalten. Sie gehen dann in die klassischen Fourieramplituden der zugehörigen ebenen Wellen über, die das klassische Feld aufbauen.
Bei Fermionen ist das anders: Aufgrund des Pauli-Prinzips gilt hier die Anti-Vertauschungsrelation \[ a a^{+} + a^{+} a = \hbar \omega \] die für verschwindendes \( \hbar \) in die Beziehung \[ a a^{+} + a^{+} a = 0 \] oder umgestellt in \[ a a^{+} = - a^{+} a \] übergeht. Hier können also \( a^{+} \) und \( a \) im klassischen Grenzfall keine Zahlen (Feldamplituden) sein, denn beim Vertauschen ergibt sich ein Vorzeichenwechsel.
Das ist wieder ein Zeichen dafür, dass es keine klassischen Fermionfelder gibt, sondern dass der klassische Grenzfall nur formalen Charakter haben kann, der lediglich als Hilfsmittel zum Formulieren einer Fermion-Quantentheorie in Analogie zur Bosonen-Quantentheorie dient.
Mathematisch bezeichnet man übrigens ein solches mathematisches Konstrukt mit Vorzeichenwechsel beim Vertauschen als Grassmann-Algebra (siehe z.B. Die Symmetrie der Naturgesetze, Kapitel 6.1).
Man kann solche Grassmann-Felder beispielsweise dazu verwenden, um die Quantisierung mithilfe von Pfadintegralen auch bei Fermionen durchführen zu können (bei Pfadintegralen ergibt jede denkbare Feldkonfiguration eine Amplitude \( e^{i S / \hbar} \) mit der klassischen Wirkung \(S\) der Feldkonfiguration, und diese Amplituden werden über alle relevanten Feldkonfigurationen aufintegriert, siehe Zusatzinfos zu Kapitel 5.5). Dabei haben nicht die Grassmann-Felder selbst, sondern nur das mit ihnen gebildete Pfadintegral eine physikalische (quantenmechanische) Bedeutung.
Braucht man generell zumindest formal klassische Fermion- und Bosonfelder, um anschließend zu einer Quantenfeldtheorie zu gelangen? Nicht unbedingt! Eigentlich verwendet man diese klassischen Felder nur dazu, um eine relativistisch invariante Wirkung \( S \) (oder alternativ eine Lagrangedichte oder eine Hamiltondichte) daraus zusammenzubauen.
Aus dieser Wirkung kann man einerseits die klassischen Feldgleichungen ableiten (Prinzip der kleinsten Wirkung, siehe Quantenfeldtheorie und Eichfelder, Kapitel 3 und Kapitel 4), andererseits aber auch quantenmechanische Amplituden berechnen, indem man die Felder in der Wirkung durch die oben erwähnten Feldoperatoren ersetzt. Wenn man sich für die klassischen Feldgleichungen nicht interessiert, so könnte man auch direkt mit Feldoperatoren statt mit klassischen Feldern beginnen, diese wie in der klassischen Wirkung zu einem relativistisch invarianten Operator zusammensetzen und damit direkt eine Quantentheorie aufbauen, ohne jemals klassische Felder bemüht zu haben.
Genau diesen Weg schlägt Steven Weinberg in seinem Buch The Quantum Theory of Fields, Vol. I ein (siehe auch die Zusammenfassung in Die Symmetrie der Naturgesetze, Kapitel 4.15).
Weinberg startet direkt mit einer relativistischen Quantentheorie freier Teilchen und konstruiert die möglichen Teilchen-Quantenzustände zu verschiedener Masse, Impuls und Spin sowie zugehörige Einteilchen-Erzeugungs- und Vernichtungs-Operatoren \( a^{+} \) und \( a \).
Das relativistische Transformationsverhalten dieser Teilchenzustände und der zugehorigen Operatoren \( a^{+} \) und \( a \) ist dabei aufgrund des Spins komplizierter als beispielsweise bei Vierervektoren, so dass es zunächst schwierig ist, relativistisch invariante Operatoren aus \( a^{+} \) und \( a \) zusammenzubauen, die man zur Beschreibung der Wechselwirkung zwischen den Teilchen braucht. Daher führt man als Hilfsgrößen entsprechende Linearkombinationen dieser Operatoren ein, die sich einfacher transformieren – das sind dann die oben erwähnten Feldoperatoren, die aber hier nicht durch eine zweite Quantisierung der klassischen Felder entstehen, sondern die man unmittelbar als Linearkombinationen der bereits vorhandenen Teilchenoperatoren konstruieren kann. Die Koeffizienten dieser Linearkombinationen sind dabei Funktionen, die die klassischen freien Feldgleichungen erfüllen, beispielsweise die freie Diracgleichung.
Die Vorgehensweise Weinbergs macht auch klar, wieso es zur Eichsymmetrie oder zur Koordinaten-Kovarianz der allgemeinen Relativitätstheorie kommen kann:
Ein masseloses Spin-1-Teilchen wie das Photon hat nur zwei Spinamplituden (Helizitäten): je eine für den Spin in oder gegen die Impulsrichtung. Ein Vierervektorfeld wie das elektromagnetische Viererpotential \( A^{\mu} \) hat jedoch vier Komponenten. Will man nun aus Spin-1-Teilchenoperatoren einen Viererpotential-Feldoperator zusammenbauen, so hat dieser überzählige Freiheitsgrade, die man mit einer Eichtransformation lokal verändern kann, ohne dass sie sich physikalisch auswirken dürfen (denn sie sind nicht durch die Spin-1-Amplituden festgelegt, siehe Zusatzinfos zu Kapitel 5.3).
Analog hat auch ein Feldoperator analog zur metrischen Matrix der allgemeinen Relativitätstheorie überzählige Freiheitsgrade, wenn man ihn aus Spin-2-Teilchenoperatoren (passend zum Graviton) zusammenbaut. Diese überzähligen Freiheitsgrade entsprechen der Tatsache, dass man in der der allgemeinen Relativitätstheorie das globale Raumzeit-Koordinatensystem ändern kann, ohne dass dies die physikalischen Gesetze ändert (siehe Zusatzinfos zu Kapitel 7.1).
Wie übersetzen sich eigentlich die Eigenschaften der klassischen Feldtheorie in die entsprechende Quantenfeldtheorie? Oben haben wir bereits gesehen, wie aus klassischen Feldern eine Gesamtheit aus Feldquanten wird. Das gilt aber in dieser Form genau genommen nur für freie Felder ohne Wechselwirkung, also beispielsweise für elektromagnetische Wellen ohne die Anwesenheit elektrischer Ladungen. Diese elektromagnetischen Wellen werden in der Quantenfeldtheorie dann durch eine Gesamtheit freier Photonen ersetzt, die nicht miteinander wechselwirken. Da für elektromagnetische Felder das Superpositionsprinzip gilt und Photonen entsprechend elektrisch neutral sind, ist das kein Problem – Photonen wechselwirken nicht miteinander (jedenfalls nicht direkt). Bei Gluonen ist das schon anders – entsprechend gibt es für sie weder klassische Felder noch die oben dargestellte Gesamtheit aus freien Gluonen, denn Gluonen wechselwirken stark miteinander. Es gibt keine Gluonen als freie Teilchen.
Freie Felder werden durch freie Wellengleichungen beschrieben, beispielsweise durch die Maxwellgleichungen ohne Ladungen und Ströme oder durch die freie Klein-Gordon- oder Dirac-Gleichung. Dabei ergibt sich ein bestimmter Zusammenhang zwischen Frequenz und Wellenlänge, der sich bei den Feldquanten in einem entsprechenden Zusammenhang zwischen Teilchenenergie- und Impuls widerspiegelt, also letztlich in einer bestimmten Teilchenmasse.
Weiterhin ergibt sich aus den freien Wellengleichungen ein bestimmtes Transformationsverhalten für die Feldkomponenten bei Lorentztransformationen (Wechsel des Raum-Zeit-Bezugssystems), d.h. man hat es beispielsweise mit skalaren Feldern, Vierervektorfeldern oder Dirac-Spinorfeldern zu tun. Dieses Transformationsverhalten der Felder überträgt sich in bestimmter Weise auf das Transformationsverhalten der Teilchenzustände und legt damit deren Spin fest. So gehören skalare Felder zu Spin 0, Vierervektorfelder zu Spin 1 und Dirac-Spinorfelder zu Spin 1/2. Genau dieser Zusammenhang zwischen Feldkomponenten und Teilchenspin wird hergestellt, wenn man aus den Einteilchen-Erzeugungs- und Vernichtungs-Operatoren \( a^{+} \) und \( a \) die Feldoperatoren per Linearkombination bildet. Dabei können ggf. Freiheiten für die Felder bestehen bleiben (Stichwort Eichsymmetrie, siehe oben).
Die Wechselwirkungen zwischen den verschiedenen Feldern (z.B. zwischen geladenen Fermionfeldern und elektromagnetischen Feldern) werden dann zumeist erst in einem zweiten Schritt in die Quantenfeldtheorie übertragen, beispielsweise im Rahmen der Störungstheorie, die letztlich zu den Feynmangraphen führt. Messbar sind dann nur die freien Teilchen / Feldquanten vor und nach der Wechselwirkung und die entsprechenden Wahrscheinlichkeitsamplituden für deren Auftreten (S-Matrix). Der innere Ablauf des Wechselwirkungsprozesses selbst kann nicht durch messbare Größen näher aufgeschlüsselt werden.
Zum Abschluss noch ein Hinweis, wie die Feynmangraphen formal entstehen:
In der klassischen Elektrodynamik wird die Wechselwirkung zwischen einer elektrischen Stromdichte \( j_{\mu} \) mit Teilchenladung \(q\) und einem elektromagnetischen Viererpotential \( A^{\mu} \) durch einen Term \[ q \, j_{\mu} A^{\mu} \] in der Wirkung dargestellt. Wenn der Strom aus geladenen Fermionen (z.B. Elektronen) besteht, kann man ihn formal durch das Fermionfeld \( \psi \) ausdrücken: \[ j_{\mu} = \bar{\psi} \gamma_{\mu} \psi \] (die genauen Details sind unwichtig – entscheiden ist, dass das Fermionfeld zweimal vorkommt). Der Wechselwirkungsterm lautet also \[ q \, \bar{\psi} \gamma_{\mu} \psi \, A^{\mu} \] In der Quantenfeldtheorie werden nun die Felder durch Feldoperatoren ersetzt, also durch Linearkombinationen aus Teilchenerzeugern und Vernichtern. So kann \(\psi\) ein ankommendes Elektron vernichten, \(A^{\mu}\) kann ein Photon erzeugen und \( \bar{\psi} \) ein neues Elektron erzeugen, so dass der Term \( q \, \bar{\psi} \gamma_{\mu} \psi \, A^{\mu} \) insgesamt einen Elektron-Photon-Vertex ergibt.
Die S-Matrix enthält nun aber nicht nur einen solchen Term, sondern eine Potenzreihe mit beliebig hohen Potenzen dieses Terms, ähnlich zur geometrischen Reihe (genauer: wie bei der Exponentialreihe). Dadurch gelingt es in der Quantenfeldtheorie, die wechselwirkenden Felder durch freie Felder auszudrücken, denen man freie Feldquanten zuordnen kann.
Die Feynmangraphen enthalten entsprechend der höheren Potenzen der Reihe einen oder mehrere Vertices, die die Wechselwirkung ausdrücken, sowie dazwischen laufende Linien, die die zwischen den Vertices frei laufenden Teilchen repräsentieren. Dabei können diese Teilchen virtuell sein, so dass ihre Energie und ihr Impuls keine feste Beziehung zueinander haben müssen, anders als bei reellen Teilchen. Übersetzt in die Fourierkomponenten des klassischen Feldes wären das Wellen, deren Frequenz und Wellenlänge nicht dieselbe Beziehung wie bei freien ebenen Wellen aufweisen muss. So kann zwar eine Wellenlänge (also ein Teilchenimpuls) vorliegen, aber die Frequenz kann Null sein (also keine Teilchenenergie) – die Welle wäre statisch und gehört zu einem statischen Gesamtfeld.
In der relativistischen Quantenfeldtheorie kann der Teilchenort nur mit einer bestimmten Genauigkeit angegeben werden, den wir im Buchkapitel als relativistische Ortsunschärfe bezeichnet haben (siehe auch oben). Im Buchkapitel wird dafür die Formel \[ \Delta x \gt \frac{\hbar c}{E} \] angegeben. Für ruhende Teilchen ist \( E = mc^{2} \) und damit \[ \Delta x \gt \frac{\hbar}{mc} \] Die Größe \( \frac{\hbar}{mc} \) hatten wir in den Zusatzinfos zu Kapitel 2.6 als (reduzierte) Compton-Wellenlänge bezeichnet:
| (reduzierte) Compton-Wellenlänge: \[ \bar{\lambda}_C = \frac{\hbar}{mc} \] |
Die (nichtreduzierte) Compton-Wellenlänge ist dann
\[
\lambda_C = \frac{h}{m c} = \frac{\bar{\lambda}_C}{2 \pi}
\]
analog zum Zusammenhang zwischen \(h\) und \(\hbar\).
Für ruhende Teilchen gilt demnach für die relativistische Ortsunschärfe \[ \Delta x \gt \bar{\lambda}_C \] d.h. die Comptonwellenlänge ist die maximal mögliche Genauigkeit, mit der der Ort eines Teilchens bestimmt werden kann.
Bei Versuchen zur noch genaueren Ortsmessungen entstehen störende Teilchen-Antiteilchen-Paare, die eine weitere Steigerung der Messgenauigkeit verhindern. Man kann es auch so ausdrücken: Die Compton-Wellenlänge ist die Längenskala, unterhalb der relativistische Effekte für die quantenmechanische Beschreibung des Elektrons wichtig werden – daher das Auftauchen der Lichtgeschwindigkeit \(c\).
Man kann die relativistische Ortsunschärfe auf verschiedene Weise begründen (siehe Buchkapitel sowie oben unter Abschnitt d). Hier ist eine weitere Variante:
Wenn wir das Wellenpaket eines Elektrons mit Masse \(m\) auf einen Raumbereich der Größe \(\Delta x\) beschränken, so entsteht eine Impulsunschärfe \(\Delta p\), welche die Heisenberg'sche Unschärferelation \[ \Delta p \, \Delta x \gt \hbar \] oder umgestellt \[ \Delta x \gt \frac{\hbar}{\Delta p} \] erfüllt (den Faktor 1/2 lassen wir bei dieser groben Abschätzung zur Vereinfachung weg).
Wenn nun die Größe des Wellenpakets und damit die Ortsunschärfe \(\Delta x\) immer weiter verringert wird, so wird die Impulsunschärfe \(\Delta p\) schließlich so groß, dass die Energie \(E\) des Elektrons ausreicht, um neue Elektron-Positron-Paare zu erzeugen: \[ E = mc^{2} + (pc)^{2} \gt mc^{2} + 2 mc^{2} \] mit \(p \approx \Delta p\). Diese Paarerzeugung beginnt also ungefähr bei \( \Delta p = mc \) (wieder lassen wir den Faktor 2 weg) und stört die Ortsmessung des alten Elektrons. Die Genauigkeit der Ortsmessung ist also ungefähr durch \[ \Delta x \gt \frac{\hbar}{\Delta p} = \frac{\hbar}{m c} = \bar{\lambda}_C \] beschränkt.
Die relativistische Ortsunschärfe \[ \bar{\lambda}_C = \frac{\hbar}{m c} \] hängt von drei Parametern ab: Dem Planck'schen Wirkungsquantum \(\hbar\), der Elektronenmasse \(m\) und der Lichtgeschwindigkeit \(c\). Die Formel für die Comptonwellenlänge entsteht gleichsam automatisch, wenn man aus diesen drei Parametern eine Längeneinheit konstruiert. An dieser Formel kann man ablesen:
In den Zusatzinfos zu Kapitel 2.6 hatten wir eine weitere Längenskala kennengelernt, in die die Elektronenmasse \(m\) eingeht: den Bohrschen Radius \[ a = \frac{\hbar^{2}}{m k e^{2}} \] der die typische Größernordnung von Atomradien angibt. Dort hatten wir auch die folgende Relation zwischen dem Bohrschen Radius \(a\) und der Compton-Wellenlänge \( \bar{\lambda}_C \) des Elektrons hergeleitet:
| \[ a = \frac{1}{\alpha} \bar{\lambda}_C \] |
Dabei ist \[ \alpha = \frac{k e^{2}}{\hbar c} \] die elektromagnetische Kopplungskonstante (siehe Buchkapitel 5.2).
Der Bohrsche Radius (0,53 Angström, also die typische Größe von Atomen) ist also etwa 137 mal größer als die Compton-Wellenlänge des Elektrons (0,004 Angström), ab der relativistische Effekte für Elektronen wichtig werden (diese Zahlenwerte hatten wir bereits in den Zusatzinfos zu Kapitel 2.6 berechnet). Halten wir fest:
| \[ \bar{\lambda}_C = 400 \, \mathrm{fm} = 0,004 \, \mathrm{Angstroem} \] |
Wir kennen sogar eine dritte Längenskala, in die die Elektronenmasse \(m\) eingeht: den klassischen Elektronenradius \[ r_{e} = \frac{k e^{2}}{m c^{2}} \] (siehe Zusatzinfos zu Kapitel 3.4). Das ist ungefähr der Radius einer geladenen Kugel mit einer Elementarladung \(e\), deren elektrische Feldenergie gerade die Elektronenmasse ergibt. Man kann dies so interpretieren, dass unterhalb dieser Längenskala Renormierungseffekte für das Elektron wichtig werden, die die Masse des Elektrons neu justieren. Dabei hatten wir die folgende Beziehung zur Compton-Wellenlänge \( \bar{\lambda}_C \) des Elektrons hergeleitet:
| \[ r_{e} = \alpha \, \bar{\lambda}_C \] |
Wir haben es hier also mit einem Dreigestirn aus drei Längenskalen zu tun, in die jeweils die Elektronenmasse eingeht und die sich jeweils um den Faktor \( \alpha = 1/137 \) unterscheiden:
Für Elektronen und ihre elektromagnetische Wechselwirkung sind diese drei Skalen wegen des Faktors \(\alpha = 1/137\) recht unterschiedlich. Bei Quarks und ihrer starken Wechselwirkung tritt die starke Kopplungskonstante \(\alpha_{s}\) an die Stelle von \(\alpha\). Sie liegt nahe bei Eins, so dass die drei Längenskalen fast zusammenfallen. Für die aus Quarks gebildeten Hadronen sind daher sowohl relativistische Efekte als auch Renormierungseffekte wichtig (man denke an die ambivalente Definition der Quarkmassen in Kapitel 4.2).
Zurück zur Compton-Wellenlänge: Quantenmechanische Gleichungen (Schrödingergleichung, Klein-Gordon-Gleichungen, Diracgleichungen) können immer so geschrieben werden, dass Massen in ihnen in Form der Compton-Wellenlänge eingehen, d.h. die Compton-Wellenlänge ist die Längenskala, über die Massen in diese Gleichungen eingehen. Betrachtet man statische Lösungen dieser Gleichungen mit Quelltermen, so kann man sehen, dass der Austausch von Teilchen mit Masse \(m\) zu Kräften führt, deren Reichweite durch die Compton-Wellenlänge dieser Teilchen gegeben ist (Stichwort Yukawa-Potential, man denke beispielsweise an den Pionaustausch bei starken Kernkräften oder an die W- und Z-Bosonen bei der schwachen Wechselwirkung; mehr dazu siehe in den Zusatzinfos zu Kapitel 5.2 Abschnitt b).
Die Compton-Wellenlänge ist historisch ein Begriff aus der sogenannten Compton-Streuung – daher der Name. Dabei trifft ein hochenergetisches Photon auf ein ruhendes Elektron (oder ein anderes geladenes Teilchen) und überträgt einen Teil seiner Energie auf dieses Elektron. Die Compton-Streuung ist also eine Verwandte des Photoeffekts, nur dass diesmal das Photon nicht verschwindet, sondern einen Teil seiner Energie behält. Konkret kann man die Compton-Streuung experimentell beispielsweise durch die Streuung von Röntgenstrahlen an den Elektronen eines Materials (z.B. Graphit) realisieren, wobei man ggf. noch die atomare Bindungsenergie des Elektrons im Atom berücksichtigen muss. Dabei ist die Compton-Streuung der dominierende Wechselwirkungsprozess von Photonen mit Materie für Photonenenergien zwischen etwa 100 keV bis 10 MeV (siehe Wikipedia: Compton-Effekt).
Die Compton-Streuung.
Credit: Herbertweidner,
Quelle:
Wikipemia: Commons File:Compton scattering-de1.png,
dort gemeinfrei.
Die Energie, die vom Photon auf das Elektron übertragen wird, hängt von dem Winkel \(\phi\) ab,
um den das Photon durch die Wechselwirkung aus seiner Flugrichtung abgelenkt wird (siehe Grafik).
Bei einer Ablenkung um 90 Grad wird die Differenz \( \Delta \lambda \)
der Photonwellenlängen vorher und nachher
gerade durch die (nichtreduzierte) Compton-Wellenlänge gegeben, wie man mithilfe der
Energie-Impuls-Erhaltung ausrechnen kann (siehe z.B. Wikipedia):
\[
\Delta \lambda = \frac{h}{mc}
\]
Ein letzter Hinweis:
Wenn wir nicht nur die elektromagnetische Wechselwirkung betrachten, sondern auch die Gravitation ins Spiel bringen, so kommt eine weitere wichtige Längenskala aus der allgemeinen Relativitätstheorie ins Spiel: der Schwarzschildradius eines schwarzen Lochs. Dieser ist proportional zur Masse des Objektes, denn je massereicher ein Objekt wird, umso stärker ist sein Gravitationsfeld.
Die Compton-Wellenlänge ist dagegen antiproportional zur Masse des Objektes, denn die relativistische Ortsunschärfe wird umso geringer, je massereicher das Objekt ist (die störenden Teilchen-Antiteilchen-Paare dieser Objektklasse entstehen dann ja erst bei höheren Energien, also kleineren Längenskalen).
Bei anwachsender Masse eines hypothetischen Teilchens kommt also irgendwann der Punkt, bei dem sein wachsender Schwarzschildradius größer als die schrumpfende Compton-Wellenlänge wird. Die entsprechende Längenskala heißt Planck-Länge und die entsprechende Masse heißt Planck-Masse.
Die Planck-Länge ist mit etwa \(10^{- 20}\) fm sehr viel kleiner als alle oben betrachteten Längen. Bei dieser winzigen Längenskala werden also Gravitationseffekte und relativistische Quanteneffekte gleich wichtig, so dass eine quantenmechanische Gravitationstheorie notwendig wird. Bildlich gesprochen: Ein schwarzes Loch von einer Planck-Masse kann nur noch mit einer Genauigkeit von einer Planck-Länge lokalisiert werden, wobei das zugleich sein Schwarzschildradius wäre. Es macht daher keinen Sinn mehr, es als klassisches schwarzes Loch im Rahmen der allgemeinen Relativitätstheorie zu beschreiben. Unterhalb der Planck-Länge beginnen virtuelle schwarze Löcher eine ähnliche Rolle zu spielen wie virtuelle Teilchen in der Quantenfeldtheorie, und sehr merkwürdige Dinge geschehen. Mehr dazu in Buchkapitel 7.2.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 17 January 2024