Zusammenfassung des Buchkapitels:
Wie können wir uns die Bewegung der Elektronenwelle im anziehenden elektrischen Feld eines Atomkerns vorstellen?
Man kann sich diese Welle grob als das dreidimensionale Analogon zu einer schwingenden Gitarrensaite oder zum hin- und her-schwappenden Wasser in einer Badewanne vorstellen. So etwas nennt man auch eine stehende Welle. Dabei können auch mehrere Schwingungsbäuche auftreten, was im Atom höheren Energieniveaus für die Elektronen entspricht.

Wo genau befindet sich nun ein Elektron zu einem bestimmten Zeitpunkt?
Die Quantenmechanik sagt dazu: Das ist unbestimmt!
Diese Situation erscheint uns ziemlich unbefriedigend zu sein. Wie kann eine Wissenschaft, die geradezu der Inbegriff einer präzisen Naturwissenschaft ist, sich mit Wahrscheinlichkeiten begnügen? Viele große Physiker des zwanzigsten Jahrhunderts wollten sich damit nicht abfinden, unter ihnen Albert Einstein. "Gott würfelt nicht!" gehört zu Einsteins bekanntesten Aussagen. Gibt es eine Möglichkeit, die statistische Beschreibung durch die Quantenmechanik zu überwinden? Mehr dazu in den nächsten Kapiteln.
a) Grafiken zur Elektronenhülle
b) Der Grundzustand im Wasserstoffatom
c) Längen- und Energieskalen für Atome, Bohrscher Radius
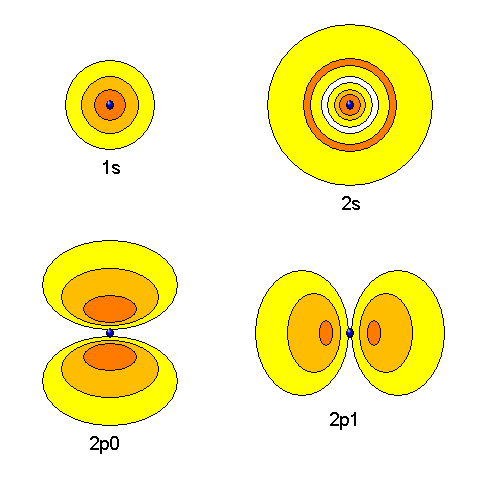
Unter Wikipedia: Wasserstoffatom habe ich folgende schöne graphische Darstellung zur Aufenthaltswahrscheinlichkeit des Elektrons in einem Wasserstoffatom (Orbitale) gefunden:
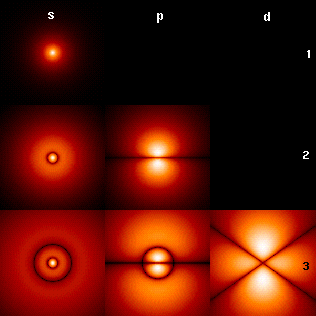
Quelle:
Wikimedia Commons File:HAtomOrbitals.png, upload: Florian Marquardt,
CC BY-SA 3.0 DEED
Man findet in
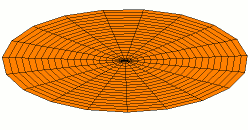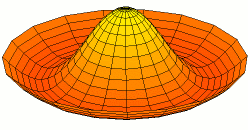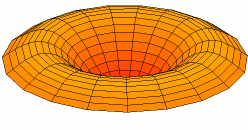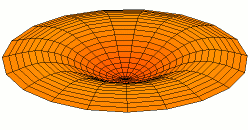
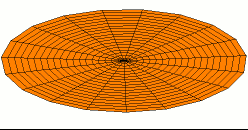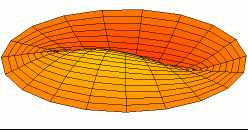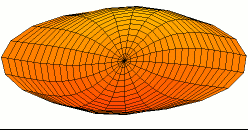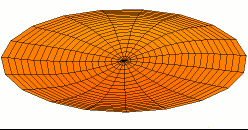
Wikimedia: Category:Drum vibration animations sehr schöne Animationen zu den entsprechenden
Schwingungen einer zweidimensionalen Membran. Hier drei Beispiele, die den 1s, 2s und 2p -Schwingungen der
Elektronenwelle entsprechen (die Stärke der Schwingungsamplitude an einem Ort ergäbe dabei die Aufenthaltswahrscheinlichkeit
für das Elektron):
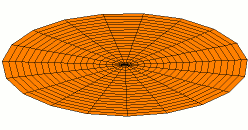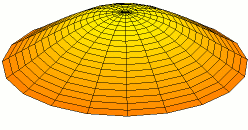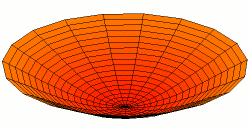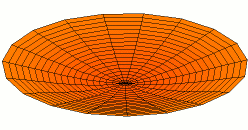
Wikimedia Commons File:Drum vibration mode01.gif,
Wikimedia Commons File:Drum vibration mode02.gif,
Wikimedia Commons File:Drum vibration mode11.gif,
alle Grafiken von Oleg Alexandrov, public domain.
Man kann die Schrödingergleichung für das Elektron im Wasserstoffatom explizit lösen – jeder Physikstudent muss da einmal durch. Das wollen wir hier nicht in aller Schönheit wiederholen, sondern uns auf den einfachsten Fall beschränken: Die Berechnung des Grundzustandes, auch 1s-Zustand genannt (siehe Grafik oben).
Ein Wasserstoffatom besteht aus zwei Teilchen: dem Proton und dem Elektron. Will man formal ganz korrekt vorgehen, so führt man zunächst Schwerpunkts- und Relativkoordinaten ein, spaltet die Schwerpunktsbewegung ab und erhält so die Schrödingergleichung für die Relativbewegung von Elektron und Proton.
Da das Proton aber etwa 2000-mal schwerer als das Elektron ist, können wir uns mit sehr guter Genauigkeit für die Relativbewegung einfach vorstellen, das Proton sei unbeweglich im Zentrum unseres Koordinatensystems festgenagelt und nur das Elektron bewege sich um das Proton herum. Außerdem wollen wir die Spins von Elektron und Proton vernachlässigen, da sie nur zu relativ kleinen Effekten führen. Wir suchen also die Elektron-Wellenfunktion \( \psi(t,\boldsymbol{x}) \), deren Betragsquadrat die Aufenthaltswahrscheinlichkeit für das Elektron am Ort \(\boldsymbol{x}\) zur Zeit \(t\) im Feld des Atomkerns angibt.
Die Schrödingergleichung eines spinlosen Teilchens in einem Potentialtopf kennen wir bereits aus Kapitel 2.3:
| \[ i \hbar \frac{d}{dt} \psi(t,\boldsymbol{x}) = \frac{1}{2m} \, \left( \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \right)^{2} \, \psi(t,\boldsymbol{x}) + \] \[ + V(\boldsymbol{x}) \, \psi(t,\boldsymbol{x}) \] |
Dabei ist \(m\) die Elektronenmasse und \[ \left( \frac{d}{d\boldsymbol{x}} \right)^{2} = \mathrm{div} \, \mathrm{grad} = \] \[ = \frac{d^2}{dx^2} + \frac{d^2}{dy^2} + \frac{d^2}{dz^2} \] der Laplace-Operator: er bildet die zweiten Ableitungen nach den drei räumlichen Koordinaten und addiert diese Ableitungen anschließend.
Im Grundzustand hat die Energie des Elektrons im Potentialtopf des Atomkerns einen festen Wert (nennen wir ihn \(E\)), so dass \( E = h f \) gilt. Die Wellenfunktion hat dann die Form
| \[ \psi(t,\boldsymbol{x}) = \psi(\boldsymbol{x}) \, e^{- \frac{i}{\hbar} E t} \] |
mit der zeitunabhängigen Wellenfunktion \( \psi(\boldsymbol{x}) \). Diese Formel zeigt, dass alle Wellenfunktionspfeile \( \psi(t,\boldsymbol{x}) \) mit derselben Frequenz synchron kreisen, so wie im Buchkapitel beschrieben.
Setzen wir diese Wellenfunktion in die Schrödingergleichung ein, so ergibt die linke Seite \[ i \hbar \frac{d}{dt} \psi(t,\boldsymbol{x}) = \] \[ = i \hbar \frac{d}{dt} \psi(\boldsymbol{x}) \, e^{- \frac{i}{\hbar} E t} = \] \[ = i \hbar \, \left(- i \frac{E}{\hbar} \right) \, \psi(\boldsymbol{x}) \, e^{- \frac{i}{\hbar} E t} = \] \[ = E \, \psi(\boldsymbol{x}) \, e^{- \frac{i}{\hbar} E t} \] Auf der rechten Seite der Schrödingergleichung können wir ebenfalls \( \psi(t,\boldsymbol{x}) = \psi(\boldsymbol{x}) \, e^{- \frac{i}{\hbar} E t} \) einsetzen und dann auf beiden Seiten \( e^{- \frac{i}{\hbar} E t} \) wegkürzen, sodass der Zeitfaktor komplett herausfällt. Für den zeitunabhängigen Anteil der Wellenfunktion ergibt sich so die Gleichung \[ E \, \psi(t,\boldsymbol{x}) = \frac{1}{2m} \, \left( \frac{\hbar}{i} \frac{d}{d\boldsymbol{x}} \right)^{2} \, \psi(\boldsymbol{x}) + \] \[ + V(\boldsymbol{x}) \, \psi(\boldsymbol{x}) \] Der Potentialtopf \( V(\boldsymbol{x}) \) ist gleich der potentiellen Energie, die das Elektron im elektrischen Feld des Atomkerns besitzt. Sie ist gegeben durch \[ V(\boldsymbol{x}) = - k \, \frac{e^{2}}{r} \] mit \[ k = \frac{1}{4 \pi \epsilon_{0}} \] und der Abstands-Koordinate \[ r = |\boldsymbol{x}| \] Warum das so ist, kann man sich folgendermaßen klar machen: Die elektrische Kraft des zentralen Protons auf das Elektron ist radial nach innen gerichtet und hat den Betrag \[ F = k \, \frac{e^{2}}{r^2} \] (Coulomb-Gesetz). Wenn wir nun den Abstand zwischen Elektron und Proton um ein sehr kleines Stück \(dr\) erhöhen, so wächst die potentielle Energie \(V(r)\) des Elektrons dadurch um den Betrag \[ dV(r) = F \, dr = k \, \frac{e^{2}}{r^2} \, dr \] d.h. es gilt \[ \frac{dV(r)}{dr} = k \, \frac{e^{2}}{r^2} \] und damit
| \[ V(r) = - k \, \frac{e^{2}}{r} \] |
Für den Grundzustand gilt weiterhin, dass die Wellenfunktion \( \psi(\boldsymbol{x}) \) nur vom Abstand \( r = |\boldsymbol{x}| \) abhängt, so dass wir \[ \psi(\boldsymbol{x}) = \psi(r) \] schreiben (es gibt auch winkelabhängige Lösungen, aber diese gehören zu angeregten Zuständen, da sie bei bestimmten Winkeln Schwingungsknotenflächen aufweisen, siehe oben die 2p-Zustände in der Grafik).
Ohne Winkelabhängigkeit ist \[ \left( \frac{d}{d\boldsymbol{x}} \right)^{2} \, \psi(r) = \frac{1}{r} \frac{d^2}{dr^2} (r \, \psi(r)) \] und wir haben \[ E \, \psi(r) = - \frac{\hbar^{2}}{2m} \, \frac{1}{r} \frac{d^2}{dr^2} (r \, \psi(r)) - k \, \frac{e^{2}}{r} \, \psi(r) \] Wir wollen uns das Leben hier einfach machen und einfach nur zeigen, dass der folgende Ansatz für den Grundzustand funktioniert (auf den Normierungsfaktor verzichten wir hier zur Vereinfachung):
| \[ \psi(r) = e^{- \frac{r}{a}} \] |
so wie im Buchkapitel angegeben (es gibt weitere Lösungen, die noch ein Polynom vor \( e^{- \frac{r}{a}} \) aufweisen, aber diese Lösungen haben eine höhere Energie, da sie angeregten Zuständen entsprechen, beispielsweise dem 2s-Zustand, siehe Grafik oben). Dazu berechnen wir \[ \frac{1}{r} \frac{d^2}{dr^2} (r \, \psi(r)) = \] \[ = \frac{1}{r} \frac{d^2}{dr^2} (r \, e^{- \frac{r}{a}}) = \] \[ = \frac{1}{r} \frac{d}{dr} \, \left( 1 - \frac{r}{a} \right) \, e^{- \frac{r}{a}} = \] \[ = \frac{1}{r} \left[ - \frac{1}{a} \, e^{- \frac{r}{a}} + \left( 1 - \frac{r}{a} \right) \left( - \frac{1}{a} \right) \, e^{- \frac{r}{a}} \right] = \] \[ = \frac{1}{r} \left[ - \frac{2}{a} + \frac{r}{a^{2}} \right] \, e^{- \frac{r}{a}} \] und setzen dies oben ein, kürzen \(e^{- \frac{r}{a}}\) weg und haben das Ergebnis: \[ E = \] \[ = - \frac{\hbar^{2}}{2m} \, \frac{1}{r} \left[ - \frac{2}{a} + \frac{r}{a^{2}} \right] - k \, \frac{e^{2}}{r} = \] \[ = - \frac{\hbar^{2}}{2m} \, \left[ - \frac{2}{ar} + \frac{1}{a^{2}} \right] - k \, \frac{e^{2}}{r} = \] \[ = \frac{1}{r} \, \left[ \frac{\hbar^{2}}{m a} - k \, e^2 \right] - \frac{\hbar^{2}}{2m} \frac{1}{a^2} \] Da dieses Ergebnis für beliebige \(r\) gilt (und da \(E\) ja konstant ist, also nicht von \(r\) abhängt), muss der Koeffizient des \(r\)-abhängigen Terms gleich Null sein, und \(E\) muss gleich dem \(r\)-unabhängigen Term sein. Das ergibt: \[ E = - \frac{\hbar^{2}}{2m} \, \frac{1}{a^{2}} \] \[ 0 = \frac{\hbar^{2}}{m a} - k \, e^2 \] Die zweite Gleichung lösen wir nach \( a \) auf: \[ k \, e^{2} = \frac{\hbar^{2}}{m a} \] und somit
| \[ a = \frac{\hbar^{2}}{m} \, \frac{1}{k e^{2}} \] \[ = \frac{\hbar}{mc} \, \frac{\hbar c}{k e^{2}} = \] \[ = \frac{\hbar}{mc} \, \frac{1}{\alpha} = \] \[ = 0,53 \, \mathrm{A} \] |
mit der elektromagnetischen Kopplunkskonstante \[ \alpha = \frac{1}{137} \] (siehe Kapitel 5.2). Man bezeichnet \( a \) auch als Bohrschen Radius (mehr dazu siehe unten unter Abschnitt c) ). Setzen wir \(a\) in unsere Formel für \(E\) ein, so erhalten wir für die Bindungsenergie des Grundzustandes im Wasserstoffatom
| \[ E = - \frac{\hbar^{2}}{2m} \, \frac{1}{a^{2}} = \] \[ = - \frac{\hbar^{2}}{2m} \, \left( \frac{mc}{\hbar} \right)^{2} \, \alpha^{2} = \] \[ = - \frac{\alpha^{2}}{2} \, m c^{2} = - 13,6 \, \mathrm{eV} \] |
Wir wollen versuchen, anders als oben im Abschnitt b) diesmal mit ganz einfachen Mitteln die Längen- und Energieskalen abzuschätzen, die für Atome wichtig sind. Dabei geht es lediglich um eine grobe Abschätzung der Größenordnung, so dass Vorfaktoren wie \(2\) oder \(\pi\) dabei keine Rolle spielen (trotzdem haben wir Glück: unsere Abschätzungen werden zufällig sogar exakt sein).
Ähnliche Überlegungen werden wir auch für relativistische Quanteneffekte (Kapitel 5.1) und Renormierungseffekte (Kapitel 3.4) wiederholen (teilweise finden sie sich auch bereits in den Buchkapiteln). Sehr lehrreich ist in diesem Zusammenhang auch im Internet der Text Length Scales in Physics von John Baez (Feburary 12, 2010).
Betrachten wir wieder das einfachste Atom: das Wasserstoffatom. Im Wasserstoffatom versucht ein Proton, über die elektrische Kraft eine Elektronenwolke möglichst eng um sich zusammenzuziehen. Dabei wird umso mehr potentielle Energie \[ E_{pot} = - k \frac{e^{2}}{r} \] frei, je kleiner der mittlere Abstand \(r\) des Elektrons vom Proton ist (in SI-Einheiten ist dabei \(k = \frac{1}{4 \pi \epsilon_{0}} \)). Diesen mittleren Abstand \(r\) kann man auch als ungefähre Ortsunschärfe \( \Delta x\) für das Elektron im Wasserstoffatom interpretieren, denn \(r\) gibt das ungefähre Ausmaß der Elektronenwolke an, in der man das Elektron irgendwo findet.
Heisenbergs Unschärferelation \[ \Delta p \, \Delta x \gt \frac{\hbar}{2} \] bewirkt nun, dass ein Schrumpfen der Elektronenwolke und damit der Ortsunschärfe eine Vergrößerung der Impulsunschärfe \( \Delta p \) und damit ein Anwachsen der mittleren kinetischen Energie \[ E_{kin} = \frac{p^{2}}{2m} \] bewirkt (\(m\) ist wieder die Elektronenmasse).
Im Grundzustand des Atoms werden \(\Delta p\) und \(\Delta x\) nicht allzu weit von den minimal erlaubten Werten entfernt sein, denn die elektrische Kraft versucht ja, die Elektronenwolke und damit \(\Delta x\) möglichst klein zu machen, während im Grundzustand zugleich auch die kinetische Energie des Elektrons möglichst klein sein wird.
Wir hatten im Buchkapitel diesen Punkt bereits angesprochen: Im Grundzustand kommt es zu einem optimalen Kompromiss zwischen kinetischer und potentieller Energie, der ein weiteres Schrumpfen der Elektronenwolke verhindert und damit das Atom stabilisiert (Details dazu gleich). Daher wird der mittlere Elektronenimpuls \(p\) ungefähr gleich der Impulsunschärfe \(\Delta p\) sein, und es gilt nach der Unschärferelation ungefähr \[ p \, r = \hbar \] (mit \( r = \Delta x \) und \( p = \Delta p \), den Faktor \(1/2\) lassen wir einfach weg).
Aus der klassischen Mechanik (Virialsatz) weiß man, dass kinetische und potentielle Energie bei diesem energetischen Kompromiss grob ungefähr gleich groß sind. Wir können aber auch ganz konkret das ungefähre Minimum von kinetischer plus potentieller Energie ausrechnen, indem wir die Abschätzung \[ p = \frac{\hbar}{r} \] aus der Unschärferelation sowie die Abkürzung \[ a = \frac{\hbar^{2}}{m k e^{2}} \] verwenden: \[ E_{ges} = E_{kin} + E_{pot} = \] \[ = \frac{p^2}{2m} + k \frac{e}{r} = \] \[ = \frac{\hbar^2}{2m r^2} + k \frac{e}{r} = \] \[ = \frac{\hbar^{2}}{2m} \, \left[ \frac{1}{r^{2}} - \frac{2m k e^{2}}{\hbar^{2}} \frac{1}{r} \right] = \] \[ = \frac{\hbar^{2}}{2m} \, \left[ \frac{1}{r^{2}} - \frac{2}{ar} \right] = \] \[ = \frac{\hbar^{2}}{2m} \, \left[ \frac{1}{r^{2}} - \frac{2}{ar} + \frac{1}{a^2} - \frac{1}{a^2} \right] = \] \[ = \frac{\hbar^{2}}{2m} \, \left[ \left( \frac{1}{r} - \frac{1}{a} \right)^{2} - \frac{1}{a^2} \right] \] Diese Formel stellt eine nach oben geöffnete Parabel in der Variable \(1/r\) dar, die ihr Minimum bei \( r = a \) aufweist. In der Variable \(r\) sieht der entsprechende Funktionsgraph so aus:
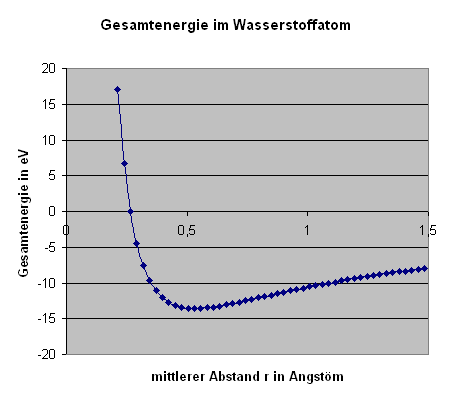
Abschätzung der Gesamtenergie des Elektrons im Wasserstoffatom
nach der obigen Formel.
Dabei ist \(r\) der mittlere Abstand des Elektrons vom Proton und \(a\) der Bohrsche Radius.
Wir sehen also, dass es tatsächlich einen mittleren Abstand \(r = a\) gibt, bei dem
es zu dem angesprochenen optimalen Kompromiss zwischen kinetischer und potentieller
Energie kommt, so dass die Gesamtenergie minimal wird.
Diesen Abstand bezeichnet man als Bohrschen Radius (siehe auch weiter oben unter Abschnitt b) ):
|
Bohrscher Radius: \[ a = \frac{\hbar^{2}}{m k e^{2}} \] |
Tatsächlich findet man auch in der quantenmechanisch präzisen Rechnung mithilfe der Schrödingergleichung, dass diese Formel für \(a\) den mittleren Radius des Wasserstoffatoms im Grundzustand korrekt angibt (siehe Abschnitt b) weiter oben).
Die obige Abschätzung zeigt auch: Würde die elektrische Anziehungskraft mit \(1/r^{3}\) oder noch stärker für schrumpfenden Abstand \(r\) anwachsen (die potentielle Energie also mit \(1/r^{2}\) oder stärker ins Negative anwachsen), so hätte die Gesamtenergie \(E_{ges}\) kein Minimum, denn die mit \(1/r^{2}\) wachsende kinetische Energie könnte die mit mehr als \(1/r^{2}\) frei werdende potentielle Energie nicht mehr ausgleichen. Das Elektron würde trotz Heisenbergscher Unschärfe in den Atomkern stürzen und Atome wären nicht stabil.
Hätte unser Raum nicht drei, sondern vier oder mehr Raumdimensionen, so wäre genau das der Fall (siehe auch die Zusatzinfos zu Kapitel 8.1 Abschnitt a. Materie und damit Leben, wie wir es kennen, wäre nicht möglich. Wer weiß – vielleicht hat unser Raum nur deswegen drei Raumdimensionen, weil jede andere Raumdimensionsanzahl die Entstehung von Leben unmöglich machen würde, so dass in solchen Universen niemand da ist, der sich Gedanken darüber machen kann. Das ist das sogenannte anthropische Prinzip. Mehr dazu in den Zusatzinfos zu Kapitel 8.1 Abschnitt b.
Der Bohrsche Radius \[ a = \frac{\hbar^{2}}{m k e^{2}} \] gibt die ungefähre Größenordnung von Atomen an. Die Skala für Atomradien hängt demnach nur von drei Parametern ab: Dem Planck'schen Wirkungsquantum \(\hbar\), der Elektronenmasse \(m\) und der elektrischen Ladung der beteiligten Teilchen, also hier der Elementarladung \(e\) (der Faktor \(k\) dient nur dazu, die Ladungseinheit im Coulombgesetz passend in eine Kraft umzurechnen – es gibt auch Einheitensysteme, in denen \(k = 1\) ist). Wenn man sich fragt, wie man aus diesen drei Parametern auf einfache Weise eine Längeneinheit konstruieren kann, so erhält man automatisch die obige Formel für \(a\). An dieser Formel für \(a\) kann man ablesen:
Ein Beispiel für die Massenabhängigkeit der Atomradien sind myonische Atome, bei denen Myonen statt Elektronen für kurze Zeit die Atomhülle bilden, bevor sie zerfallen. Myonische Atome sind etwa 200 mal kleiner als normale Atome, denn Myonen sind etwa 200 mal schwerer als Elektronen.
Umgekehrt: Positronium ist ein kurzlebiger gebundener Zustand aus einem Positron und einem Elektron (siehe auch Buchkapitel 5.2). Das schwere Proton wird also durch das 2000-mal leichtere Antiteilchen des Elektrons ersetzt: das Positron. Anders als beim Wasserstoffatom darf man in Positronium die Bewegung des Positrons daher nicht mehr vernachlässigen, sondern muss zu sogenannten Relativkoordinaten übergehen. Dabei entsteht eine Gleichung für die Relativkoordinate \(r\), in der die sogenannte reduzierte Masse \( m_{r} \) an die Stelle der Elektronenmasse \(m\) tritt. Bei einem gebundenen System aus zwei Teilchen mit Massen \(m_{1}\) und \(m_{2}\) ist die reduzierte Masse gegeben durch \[ \frac{1}{m_{r}} = \frac{1}{m_{1}} + \frac{1}{m_{2}} \] d.h. ihr Kehrwert ist die Summe der beiden Massen-Kehrwerte. Im Wasserstoffatom ist die Protonmasse etwa 2000 mal größer als die Elektronenmasse, so dass \(m_{r}\) fast gleich der Elektronenmasse \(m\) ist. Bei Positronium ist dagegen \[ \frac{1}{m_{r}} = \frac{1}{m} + \frac{1}{m} = \frac{2}{m} \] d.h. \[ m_{r} = \frac{m}{2} \] Der mittlere Abstand zwischen Elektron und Positron in Positronium ist daher doppelt so groß wie der mittlere Abstand zwischen Elektron und Proton im Wasserstoffatom.
Die Lichtgeschwindigkeit \(c\) taucht in der Formel für den Bohrschen Radius nicht auf, denn diese Formel basiert auf der nichtrelativistischen Quantenmechanik. Um den konkreten Zahlenwert für den Bohrschen Radius zu berechnen, ist es dennoch nützlich, die Lichtgeschwindigkeit \(c\) als Hilfsgröße mit ins Spiel zu bringen und den Bohrschen Radius so mit einer anderen (relativistischen) Länge in Beziehung zu bringen: der (reduzierten) Compton-Wellenlänge des Elektrons:
| (reduzierte) Compton-Wellenlänge: \[ \bar{\lambda}_C = \frac{\hbar}{m c} \] |
Die (nichtreduzierte) Compton-Wellenlänge ist dann \[ \lambda_C = \frac{h}{m c} = 2 \pi \, \bar{\lambda}_C \] analog zum Zusammenhang zwischen \(h\) und \(\hbar\). Die Compton-Wellenlänge ist die Längenskala, unterhalb der relativistische Effekte für die quantenmechanische Beschreibung des Elektrons wichtig werden – daher das Auftauchen der Lichtgeschwindigkeit \(c\). In Buchkapitel 5.1 hatten wir die Compton-Wellenlänge auch als relativistische Ortsunschärfe bezeichnet. Mehr zur Compton-Wellenlänge in den Zusatzinfos zu Kapitel 5.1.
Den Zusammenhang zwischen Bohrradius und Compton-Wellenlänge erhalten wir nun folgendermaßen: \[ a = \frac{\hbar^{2}}{m k e^{2}} = \] \[ = \frac{\hbar c}{k e^{2}} \frac{\hbar}{m c} = \] \[ = \frac{1}{\alpha} \, \bar{\lambda}_C \] d.h. wir haben
| \[ a = \frac{1}{\alpha} \, \bar{\lambda}_C \] |
Dabei ist \[ \alpha = \frac{k e^{2}}{\hbar c} \] die elektromagnetische Kopplungskonstante (auch Feinstrukturkonstante genannt, siehe Buchkapitel 5.2 ). Sie gibt das Quadrat der Elementarladung in natürlichen Einheiten an. Ihr experimenteller Wert ist \[ \alpha = \frac{1}{137} \] Der Bohrsche Radius ist also etwa 137-mal größer als die Compton-Wellenlänge des Elektrons, ab der relativistische Effekte wichtig werden. Die Atomhülle aus Elektronen lässt sich also zumindest für leichte Atome gut durch die nichtrelativistische Quantenmechanik beschreiben. Die elektromagnetische Wechselwirkung zwischen Atomkern und Elektronen ist schwach genug, denn die elektromagnetische Kopplungskonstante \(\alpha\) ist deutlich kleiner als 1.
Bei der starken Wechselwirkung wird das anders sein, ebenso bei den energetisch tiefsten Elektronenzuständen (1s-Elektronen) sehr schwerer Atome mit entsprechend großer elektrischer Kernladung (z.B. Blei). Die Ausdehnung dieser Elektronenwolken schrumpft mit der Zahl \(Z\) der Protonen im Kern, und der beträgt bei Blei bereits \(82\). Damit gerät die Ausdehnung der tiefsten Elektronenzustände in den Bereich der Compton-Wellenlänge, so dass relativistische Effekte wichtig zu werden beginnen, beispielsweise virtuelle Elektron-Positron-Paare.
Die reduzierte Compton-Wellenlänge des Elektrons beträgt ungefähr \[ \bar{\lambda}_C = \frac{\hbar}{m c} = \] \[ = \frac{\hbar c}{m c^2} = \] \[ = \frac{200 \, \mathrm{MeV} \, \mathrm{fm}}{0,5 \, \mathrm{MeV}} \] \[ = 400 \, \mathrm{fm} = 0,004 \, \mathrm{A} \] (siehe auch in Buchkapitel 5.1 die Tabelle mit den relativistischen Ortsunschärfen). Der Bohrsche Radius beträgt entsprechend ungefähr
| \[ a = 137 \cdot 0,004 \, \mathrm{A} = 0,53 \, \mathrm{A} \] |
Die Energie des Elektrons im Wasserstoffatom können wir ebenfalls mithilfe unserer obigen Formeln abschätzen. Für \(r = a\) ist \[ E_{ges} = = \frac{\hbar^{2}}{2m} \, \left[ \left( \frac{1}{r} - \frac{1}{a} \right)^{2} - \frac{1}{a^2} \right]_{r=a} = \] \[ = - \frac{\hbar^{2}}{2m} \frac{1}{a^2} = \] \[ - \frac{\hbar c}{2} \frac{\hbar}{mc} \frac{1}{a^2} = \] \[ = - \frac{\hbar c}{2} \, \bar{\lambda}_C \, \frac{1}{a^2} = \] \[ = - \frac{\hbar c}{2} \, \alpha \, a \, \frac{1}{a^2} = \] \[ = - \frac{\hbar c}{2} \, \alpha \, \frac{1}{a} = \] \[ = - 1000 \, \mathrm{eV} \, \mathrm{A} \, \frac{1}{137} \, \frac{1}{0,53 \, \mathrm{A}} = \] \[ = - 13,7 \, \mathrm{eV} \] Die Abschätzung ergibt sogar tatsächlich den exakten Wert für die Grundzustandsenergie des Wasserstoffatoms (siehe Abschnitt b oben – Glück gehabt ... ), wobei das negative Vorzeichen angibt, dass man diese Energie aufwenden muss, um das Elektron aus dem Wasserstoffatom herauszulösen. Allgemein liegen die Energien, die für die äußeren Elektronen der Atomhülle und damit für chemische Prozesse verantwortlich sind, im Elektronenvolt-Bereich.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 17 January 2024