Kapitel 6
Quarks, Computer und das Challenger-Unglück

2  Computer

• Parallelcomputer und die Connection Machine

  Feynman hatte seine erste intensive Berührung mit Computern bereits im Jahr 1944 während des Manhattan-Projekts in Los Alamos. In den 1980er Jahren konnte es sich Feynman mit seinen über sechzig Lebensjahren endlich erlauben, all seinen Computerinteressen ganz nach Lust und Laune nachzugehen. Dabei hielt Feynman am Caltech in den Jahren seit 1981 unter Mitwirkung einiger anderer Wissenschaftler eine Reihe von Vorlesungen, die im Jahr 1996 unter dem Titel Feynman Lectures on Computation auch in Buchform veröffentlicht wurden.

  Neben seinen Vorlesungen und theoretischen Untersuchungen befasste sich Feynman auch ganz praktisch mit Computern. Besonders interessierte ihn die Frage, wie man eine Aufgabe auf mehrere Prozessoren verteilen und parallel abarbeiten konnte. Hier gab es ein Projekt, das der junge Computerexperte Danny Hillis gestartet hatte. Hillis wollte einen neuen Typ von Parallelcomputer bauen, dessen Rechenleistung dank vielen Tausend Prozessoren so enorm sein sollte, dass er zu typisch menschlichem Denken in der Lage wäre − also eine wirklich intelligente Maschine.

  Feynmans Sohn Carl, der zu dieser Zeit wie Hillis ebenfalls am MIT war und dort Computerwissenschaften studierte, half Hillis bei seinem Vorhaben. Schließlich gründete Hillis im Jahr 1983 eine Firma mit dem vielversprechenden Namen Thinking Machines Corporation, um sein Projekt in die Tat umzusetzen und den Parallelcomputer zu bauen, den er Connection Machine nannte − und Richard Feynman willigte ein, als Berater für die neue Firma zu arbeiten.

  Ein Problem beim Design des Parallelcomputers bestand in der Frage, wie der Router zwischen den Prozessoren beschaffen sein musste und wieviele Zwischenpuffer man für den Datenverkehr brauchte. Die Computerexperten hatten ermittelt, dass man pro Prozessor sieben Puffer benötigte. Laut Feynmans Analyse reichten dagegen fünf Puffer aus − eine wichtige Vereinfachung beim Design des Computers..

  Feynman beschränkte sich aber keineswegs auf die Lösung dieses Routerproblems, sondern er entfaltete eine Vielzahl von Aktivitäten. So half er mit, die Zusammenarbeit unter den Computerexperten der Firma zu organisieren. Hier kam ihm seine Erfahrung aus Los Alamos zu Gute.

• Zelluläre Automaten: Einfache Regeln ergeben komplexes Verhalten

  Das allererste Programm, das im April 1985 auf der Connection Machine lief, war das Spiel des Lebens (Game of Life) – der englische Mathematiker John Horton Conway hatte es im Jahr 1970 erfunden. Eigentlich ist es gar kein Spiel, sondern ein zweidimensionaler zellulärer Automat − also eine künstliche Welt, die man sich wie ein sehr großes kariertes Blatt Papier vorstellen kann. Jedes Kästchen − auch Zelle genannt − kann dabei entweder schwarz oder weiß sein, oder anders ausgedrückt: die Zelle kann lebendig oder tot sein (daher der Name). Mehr zu den Regeln dieses Spiels siehe z.B. unter Wikipedia: Conways Spiel des Lebens.

  Die einfachen Regeln im Spiel des Lebens führen je nach Startmuster zu ganz unterschiedlichen, sich ständig verändernden Mustern, die sehr komplex werden können und sich teilweise sogar chaotisch weiterentwickeln. Kaum zu glauben, was einige wenige einfache Regeln auf einem Gitter alles hervorbringen können!

  
  

  
  Ein sogenannter Gleiter im Spiel des Lebens.
  Quelle: Wikimedia Commons File:Animated glider emblem.gif
  Credit: Quuxplusone in der Wikipedia auf Englisch, gemeinfrei

  
  Mit dem jungen britischen Physiker und Mathematiker Stephen Wolfram gab es jemanden im Beraterteam der Thinking Machines Corporation, der sich gut mit zellulären Automaten und ihren Anwendungen auskannte. Wolfram zeigte im Sommer 1985 Feynman einen besonders interessanten zellulären Automaten, den er selbst zwei Jahre zuvor gefunden hatte. Dieser Automat trägt den Namen Regel 30 (Rule 30, siehe Wikipedia: Regel 30).

  Interessanterweise führt das sehr einfache Regelwerk dieses Automaten zu einem sehr komplexen Verhalten. Feynman und Wolfram rätselten gemeinsam herum, wie es die einfache Regel 30 schaffen kann, eine so komplexe Struktur zu erzeugen − vergeblich. Schließlich nahm Feynman Wolfram verschwörerisch zur Seite nahm und fragte, woher zur Hölle er denn gewusst habe, dass Regel 30 all diese verrückten Dinge tun würde. „Du kennst mich“, antwortete Wolfram. „Ich wusste es nicht. Ich ließ einfach einen Computer alle möglichen Regeln ausprobieren. So fand ich Regel 30.“ Feynman war erleichtert: „Jetzt fühle ich mich schon viel besser. Ich dachte schon, du hättest einen Weg gefunden, es zu verstehen.“

• Die Natur simulieren – ist die Welt ein Computer?

  Könnte es sein, dass die Natur selbst gar nicht kontinuierlich ist? Sind Raum und Zeit vielleicht auf ihrer untersten Ebene ähnlich wie ein zellulärer Automat aufgebaut, sodass sich die bekannten Naturgesetze erst als Mittelung über das mikroskopische Verhalten der einzelnen Zellen ergeben?

  Solche Gedanken beschäftigten Feynman schon seit einiger Zeit. Er begann sich ganz allgemein zu fragen, ob sich die Naturgesetze auf einem Computer simulieren lassen, und wie ein solcher Computer aussehen muss. Ist das Universum vielleicht selbst nichts anderes als ein gigantischer Computer?

  Im Jahr 1981 hielt Feynman auf einer Konferenz am MIT zum Thema Physics of Computation einen bemerkenswerten Plenarvortrag mit dem Titel Simulating Physics with Computers. In diesem Vortrag diskutiert Feynman die Frage, ob es einen universellen Computer geben könne, der in der Lage ist, die physikalischen Naturgesetze absolut exakt zu simulieren und dabei nur mit dem simulierten Raumvolumen und der simulierten Zeitspanne zu skalieren. Geht das?

  In der klassischen Physik ist eine solche exakte Computersimulation nicht möglich, da sie auf kontinuierlichen Größen basiert, beispielsweise auf den Orts- und Zeitkoordinaten von Teilchen oder der Amplitude von Quantenwellen. Ein Computer kann aber immer nur mit endlich vielen Dezimalstellen arbeiten.

  Allerdings könnte die bekannte Physik mit ihren kontinuierlichen Größen womöglich nur eine Näherung sein. Vielleicht ist die wahre Physik in ihrem tiefsten Inneren diskret. Der Raum könnte aus einzelnen Punkten oder Zellen bestehen und die Zeit könnte in Sprüngen voranschreiten. Feynman mochte die Idee. Tatsächlich spricht vieles dafür, dass Planck-Länge und Planck-Zeit die kleinsten Raum- und Zeitabstände sind, die physikalisch noch sinnvoll sind.

• Die Frage der Zeitsymmetrie: reversibles Rechnen

  Ein weiteres Problem könnte darin liegen, dass die grundlegenden Naturgesetze im Wesentlichen reversibel − also zeitsymmetrisch − sind. Damit ein Computer eine zeitsymmetrische Natur exakt simulieren kann, muss der entsprechende Rechenvorgang in ihm ebenfalls zeitlich umkehrbar sein. Bei den heute gängigen Computerarchitekturen ist das nicht der Fall. Man kann die Computerarchitektur aber ändern, indem man darauf achtet, beim Rechenvorgang keine Informationen zu verlieren, sodass der Rechenvorgang auch umgekehrt ablaufen kann (also aus den Ergebnissen die Eingaben errechnet).

• Simulation von Raum und Zeit

  Wie sieht es mit der Simulation der Zeit selbst aus? Wenn wir annehmen, dass die Zeit nicht kontinuierlich, sondern in Sprüngen abläuft, dann kann beispielsweise ein zellulärer Automat dies mit seinen Schritten von Generation zu Generation gut simulieren. Genau genommen imitiert aber laut Feynman der Computer die Zeit dabei nur. Die Zeit könnte jedoch komplizierter sein, sodass ein reines Imitieren nicht ausreicht.

  In der klassischen Physik sollte so etwas Kompliziertes aber nicht auftreten: Die klassische Physik ist kausal und reversibel, d. h., die unmittelbare Vergangenheit bestimmt die Zukunft und umgekehrt. Zugleich ist sie lokal, d. h., wenn wir von einer diskreten Struktur von Raum und Zeit ausgehen, bestimmen nur die Nachbarzellen den nächsten Zustand einer Zelle. „Wir haben offenbar zumindest im Prinzip kein Problem damit“, meint Feynman.

• Quanten und Computer

  Nun funktioniert die Natur aber nicht nach den Regeln der klassischen Physik, sondern nach den Gesetzen der Quantenmechanik.

  Die Quantenmechanik macht Aussagen über Wahrscheinlichkeiten. Es ist dabei gar nicht notwendig, dass sich der Computer exakt so wie die Natur verhält. Man kann viel mehr das reale Experiment und die zugehörige Simulation auf dem Zufallscomputer sehr oft wiederholen und die entsprechend ermittelten Häufigkeiten für die verschiedenen Ergebnisse miteinander vergleichen. Bei einer exakten Simulation müssen sie statistisch umso besser übereinstimmen, je öfter man Experiment und Simulation wiederholt.

  Kann man mit einem solchen Zufallscomputer das quantenmechanische Verhalten der Natur exakt simulieren? Wir fordern dabei, der Computer lokal arbeitet, ähnlich wie unsere zellulären Automaten.

• Den Elektronenspin simulieren

  Schauen wir uns als typisches Beispiel aus der Quantenwelt wieder den Spin eines Elektrons an. Der Spin bewirkt, dass in einem inhomogenen Magnetfeld das Elektron immer entweder in oder gegen die Richtung der magnetischen Feldlinien gezogen wird (den Einfluss der elektrischen Ladungen ignorieren wir dabei). Lässt man einen Strahl aus Elektronen also durch ein inhomogenes Magnetfeld fliegen, so teilt er sich in zwei Teilstrahlen auf.

  Ob ein einzelnes Elektron in die eine oder die andere Richtung abgelenkt wird, kann man nicht vorhersagen – es erfolgt zufällig mit gewissen Wahrscheinlichkeiten. Diese Wahrscheinlichkeiten können sich ändern, wenn wir das Magnetfeld kippen. Wenn man aber den jeweiligen quantenmechanischen Spinzustand eines Elektrons kennt, so kann man all diese Ablenkwahrscheinlichkeiten in die verschiedenen Raumrichtungen berechnen und auch in einem Computer simulieren (siehe auch die Zusatzinfos unten).

• Verschränkte Spins und spukhafte Fernwirkung

  Es gibt in der Quantenmechanik ein Phänomen, das es in der klassischen Physik so nicht gibt: die sogenannte Verschränkung von Teilchen. Schauen wir uns ein konkretes Beispiel an und stellen uns vor, dass eine Elektronenquelle immer wieder zwei Elektronen in entgegengesetzte Richtungen aussendet. Die Spins der Elektronen sollen sich dabei in einem speziellen verschränkten Zustand befinden, d. h., die Elektronen sollen sich wie entgegengesetzte Zwillinge verhalten: Wird das eine Elektron in einem senkrechten Magnetfeld nach oben abgelenkt, so wird das andere Elektron garantiert nach unten abgelenkt und umgekehrt. Dabei ist es egal, wie weit sich die beiden Elektronen bereits voneinander entfernt haben. Dasselbe Verhalten soll auch für alle anderen Ausrichtungen des Magnetfelds gelten.

  Woher weiß nun das eine Elektron, dass sich sein Partnerteilchen beispielsweise für die Ablenkung nach oben entschieden hat und es sich selbst daher nach unten orientieren muss? Eine entsprechende Nachricht müsste sich notfalls augenblicklich über beliebig große Distanzen hinweg ausbreiten − es ist aber maximal Lichtgeschwindigkeit möglich.

• Verborgene lokale Variablen: Ist die Quantenmechanik unvollständig?

  In einer gemeinsamen Arbeit aus dem Jahr 1935 sahen Albert Einstein, Boris Podolsky und Nathan Rosen diese spukhafte Fernwirkung als Beleg dafür an, dass die Quantenmechanik unvollständig sein müsse: Da diese Fernwirkung Überlichtgeschwindigkeit erfordert und demnach nicht existieren kann, muss jedes der beiden Elektronen die Information, wie es im Magnetfeld reagieren soll, bereits wie eine innere Eigenschaft mit sich tragen. Die Information muss lokal am Ort des Elektrons vorliegen, und die Quantenmechanik spiegelt diese Information nicht wider.

  Um herauszuarbeiten, wie sich eine solche innere Eigenschaft der Elektronen auswirkt, stellt Feynman in seinem Vortrag eine komplexe Überlegung an, die im Buch widergegeben ist. Dabei kommt heraus, dass die innere Eigenschaft zu einem anderen Zufallsverhalten der beiden verschränkten Elektronen führt, als wir sie beobachten. Die Quantenmechanik sagt die beobachteten Wahrscheinlichkeiten dagegen korrekt voraus!

• Nichtlokale Quantenwelt

  Ursprünglich stammen Überlegungen dieser Art von dem nordirischen Physiker John Stewart Bell, der im Jahr 1964 die berühmte Bell’sche Ungleichung aufstellte.

  Es folgt, dass das Elektron die mitgeführte lokale Eigenschaft nicht besitzen kann. Es kann keine im Elektron lokal verborgene Variable geben, die sein Verhalten in jedem Magnetfeld eindeutig festlegt. Das voneinander abhängige Verhalten der beiden Elektronen lässt sich so nicht erklären.

  Wenn wir weiterhin Überlichtgeschwindigkeit ausschließen wollen, so folgt daraus, dass die Natur sich nicht lokal verhält: Das Verhalten zweier Teilchen kann über beliebig große Entfernungen miteinander gekoppelt sein, ohne dass sie einander benachrichtigen oder ihr Verhalten bereits in der Teilchenquelle präzise aufeinander abstimmen und diese Information dann mit sich tragen. Damit geht das quantenmechanische Zufallsverhalten über das klassisch mögliche lokale Zufallsverhalten hinaus.

  Eine mögliche Lösung wäre ein Computer, der selbst auf den Regeln der Quantenmechanik basiert − also ein Quantencomputer oder Quantensimulator. Solche quantenmechanischen Computer und Simulatoren werden aktuell intensiv erforscht.

  Feynman sagt am Ende seines Vortrags, er habe schon immer Spaß daran gehabt, die begrifflichen Schwierigkeiten der Quantenmechanik immer weiter auf möglichst einen einzigen Knackpunkt hin zu verdichten. Die Zufälligkeiten in der Quantenmechanik sind demnach von anderer Art als die Zufälligkeiten in der lokalen klassischen Physik. Aber was steckt wirklich dahinter? „Eine sehr interessante Frage ist der Ursprung der Wahrscheinlichkeiten in der Quantenmechanik“, schreibt Feynman und meint weiter: „Die Natur ist nicht klassisch, und wenn man eine Simulation der Natur machen will, so sollte man sie besser quantenmechanisch machen, und es ist ein wunderbares Problem, denn es scheint nicht ganz einfach zu sein.“

Zusatzinformationen:

a) Wieviel Information passt in ein Raumvolumen?
b) Den Elektronenspin simulieren: komplementäre Informationen
c) Verschränkte Spins im Kegelmodell
d) Ablenkwahrscheinlichkeit bei einer Spinkippung um 60 Grad

a) Wieviel Information passt in ein Raumvolumen?

Nach dieser Formel ist die Entropie S eines schwarzen Lochs proportional zur Fläche A des Ereignishorizontes, der das schwarze Loch umschließt. Man kann zeigen, dass dies die maximale Entropie ist, die sich in dem Raumvolumen unterbringen lässt, das von dem Ereignishorizont umschlossen wird. Fügt man Materie mit weiterer Entropie hinzu, so wächst der Ereignishorizont und damit das von ihm umschlossene Volumen.

Nun kann man die Entropie eines Objekts auch als ein Maß für die Information ansehen, die sich in seiner mikroskopischen Struktur verbirgt. Wenn es also eine Obergrenze für die Entropie in einem Raumvolumen gibt, so gibt es auch eine Obergrenze für die Informationsmenge, die sich darin unterbringen lässt. Interessanterweise wächst diese Informations-Obergrenze nach Hawkings Formel nicht proportional zum Volumen an, sondern nur proportional zu dessen Oberfläche A. Warum das so ist, kann heute noch niemand genau sagen, auch wenn es einige interessante Ideen dazu aus der Stringtheorie oder der Loop-Quantengravitation gibt.

b) Den Elektronenspin simulieren: komplementäre Informationen

Der quantenmechanische Zustand, der durch die beiden Amplituden beschrieben wird, enthält aber mehr Informationen als nur diese beiden Wahrscheinlichkeiten. Das ist ein sehr wichtiger Punkt, den man leicht übersehen kann!

Besonders deutlich wird das, wenn wir den Spin um 90 Grad bzw. um 270 Grad nach rechts kippen − der zweite Fall entspricht natürlich einer Kippung um 90 Grad nach links. Was dabei mit den beiden Amplituden geschieht, haben wir in Kapitel 6.1 gesehen: Sie lauten ψ_↑ = 1/√2 und ψ_↓ = 1/√2 für die Kippung um 90 Grad sowie ψ_↑ = −1/√2 und ψ_↓ = 1/√2 für die Kippung um 270 Grad. Das Betragsquadrat dieser Amplituden ist also hier beides Mal gleich 1/2.

In beiden Fällen ist also die Wahrscheinlichkeit für Spin ↑ oder ↓ jeweils 50 %. Aber in einem waagerecht orientierten Magnetfeld werden die um 90 Grad gekippten Spins ausschließlich nach rechts und die um 270 Grad gekippten Spins ausschließlich nach links abgelenkt. Sie verhalten sich also unterschiedlich! Bezüglich der waagerechten Richtung würden wir die gekippten Spin daher im ersten Fall durch die Amplituden ψ_→ = 1 und ψ_← = 0 sowie im zweiten Fall durch ψ_→ = 0 und ψ_← = 1 beschreiben. Zusammengefasst haben wir also:

• θ = 90 Grad:   ψ_↑ = 1/√2 und ψ_↓ = 1/√2   entspricht   ψ_→ = 1 und ψ_← = 0

• θ = 270 Grad:   ψ_↑ = −1/√2 und ψ_↓ = 1/√2   entspricht   ψ_→ = 0 und ψ_← = 1

Es kommt also auf das Vorzeichen der beiden Amplituden relativ zueinander an, wenn man das Spinverhalten in verschiedenen Ausrichtungen des Magnetfeldes betrachtet. Das Betragsquadrat alleine genügt nicht.

Aus Kapitel 5.3 kennen wir ein anderes Beispiel, bei dem das relative Vorzeichen der Amplituden oder allgemeiner die relative Ausrichtung der Amplitudenpfeile wichtig war: die Interferenz der beiden Elektronenwellen im Doppelspaltversuch hinter den beiden Löchern. Dort bedeutete Interferenz, dass man einfach am Detektorschirm die Amplituden der beiden Teilwellen zur Amplitude der Gesamtwelle addieren muss.

Bei den Spins ist das etwas komplizierter: Interferenz der beiden Amplituden ψ_↑ und ψ_↓ bedeutet hier, dass sich aus ihnen beispielsweise bezüglich der waagerechten Richtung die beiden Amplituden ψ_→ und ψ_← so ergeben, wie wir uns das gerade überlegt haben. Wieso man hier ähnlich wie im Doppelspaltversuch von Interferenz sprechen kann, wird an folgendem Experiment deutlich, das Feynman in ähnlicher Form in seinen Lectures in Band 3 Kapitel 5-5 beschreibt:

Wir starten mit einem Strahl Elektronen, deren Spin nach rechts orientiert ist, sodass ψ_→ = 1 und ψ_← = 0 ist. In einem passenden waagerechten Magnetfeld würden diese Elektronen also nach rechts abgelenkt. Stattdessen schicken wir den Strahl aber durch ein senkrechtes Magnetfeld, sodass es zwei Möglichkeiten gibt: Die Elektronen können nach oben oder unten abgelenkt werden, so wie sie im Doppelspaltversuch durch das eine oder andere Loch hindurchgehen können. Anschließend bringen wir die beiden Teilstrahlen durch ein umgekehrtes senkrechtes Magnetfeld wieder zusammen, sodass sie sich wieder zu einem einzigen Strahl vereinen.

Was geschieht, wenn wir den wiedervereinigten Strahl nun durch ein waagerechtes Magnetfeld schicken? Er verhält sich so, als sei zwischendurch nichts weiter passiert: Die Elektronen werden wieder nach rechts abgelenkt, d.h. die beiden Amplituden ψ_↑ = 1/√2 und ψ_↓ = 1/√2 der beiden Teilstrahlen interferieren zu ψ_→ = 1 und ψ_← = 0.

Analog ist es, wenn wir mit Elektronen starten, deren Spin nach links orientiert ist, sodass wir ψ_→ = 0 und ψ_← = 1 haben. Die entsprechenden Amplituden bezüglich der senkrechten Ablenkrichtung ψ_↑ = −1/√2 und ψ_↓ = 1/√2 interferieren nach der Wiedervereinigung der Teilstrahlen wieder zu ψ_→ = 0 und ψ_← = 1, sodass die Elektronen im waagerechten Magnetfeld nach links abgelenkt werden.

Das alles stimmt allerdings nur, wenn wirklich nichts weiter passiert als eine sanfte Aufteilung und Wiedervereinigung der Strahlen in senkrechter Richtung. Beides muss so ablaufen, dass die Ablenkung der Elektronen nach oben oder unten keinerlei Spuren hinterlässt, aus denen man ablesen kann, welche der beiden Möglichkeiten gewählt wurde. Es ist wie bei den beiden Löchern im Doppelspaltversuch: Interferenz von Amplituden, die zu verschiedenen Möglichkeiten gehören, gibt es nur dann, wenn die Möglichkeiten ununterscheidbar sind.

Würden wir beispielsweise eine starke Lichtquelle im Magneten anbringen, die uns erkennen lässt, ob die Elektronen nach oben oder unten abgelenkt wurden, so zerstören wir damit die Interferenz. Wir würden dann feststellen, dass die Elektronen in beiden Fällen mit je 50 % Wahrscheinlichkeit nach oben oder unten abgelenkt werden − egal ob der Spin zuvor nach rechts oder links zeigt. Treffen sie nach der Wiedervereinigung auf das waagerechte Magnetfeld, so ist die Chance, nach rechts oder links abgelenkt zu werden, ebenfalls 50 %. Die Messung, ob die Elektronen nach oben oder unten abgelenkt werden, zerstört die Information darüber, dass der Spin nach rechts bzw. links orientiert war.

Wir sehen hier ein weiteres Beispiel für das Wirken von Heisenbergs Unschärferelation: Die Information darüber, ob der Spin in senkrechter Richtung nach oben oder unten orientiert ist, ist komplementär zu der Information, ob der Spin in waagerechter Richtung nach links oder rechts orientiert ist. Es verhält sich beim Spin ganz analog wie bei den komplementären Größen Ort und Impuls eines Teilchens: Beides zugleich kann man nicht präzise wissen. Es kann immer nur eine der beiden Informationen mit absoluter Gewissheit in den Wahrscheinlichkeitsamplituden kodiert sein. Je genauer man die eine Information hat, umso ungenauer wird die dazu komplementäre Information.

Solange man sich den Spin eines Elektrons wie einen eindeutig definierten klassischen Drehimpuls vorstellt, ist dieses typische Quantenverhalten nur schwer zu verstehen. Man kann das klassische Bild aber etwas abwandeln, sodass es die Quanteneigenschaften besser widerspiegelt. Wenn wir Glück haben, könnte dieses abgewandelte Bild womöglich eine geeignete Grundlage darstellen, um den Spin in exakter Weise in unserem Zufallscomputer zu simulieren.

Beginnen wir wieder mit einem Elektron, dessen Spin nach rechts zeigt. Ein solches Elektron würden wir uns bisher wie eine kleine Kugel vorstellen, die von rechts gesehen gegen den Uhrzeigersinn um die waagerechte Achse rotiert. Der Drehimpuls dieser Kugel würde also nach rechts zeigen. Warum man bei diesem Elektron in senkrechter Richtung mit je 50 % Wahrscheinlichkeit einen Spin nach oben oder unten messen würde, ist dann ein Rätsel. Daher verändern wir das Bild folgendermaßen: Wir stellen uns eine Kegelfläche vor, die ihre Spitze am Ort des Elektrons hat und sich von dort in die Richtung des Spins − hier also nach rechts − öffnet. Dabei bildet sie mit der z-Achse nach oben und unten einen Winkel von 45 Grad. Der Drehimpulspfeil der rotierenden Kugel soll nun nicht mehr genau nach rechts zeigen, sondern irgendwo auf der Kegelfläche liegen. Dabei können wir uns vorstellen, dass der Drehimpuls wie bei einem Kreisel ständig sehr schnell auf der Kegelfläche entlangwandert oder dort zufällig herumhüpft. Die Projektion des Drehimpulses auf die waagerechte Richtung nach rechts bleibt dabei konstant, was wir so interpretieren wollen, dass wir in der waagerechten Richtung immer den Spin nach rechts orientiert vorfinden. Die Projektion auf die senkrechte z-Achse ändert sich dagegen ständig, sodass wir in dieser Richtung den Spin zufällig mal nach oben und mal nach unten orientiert messen würden.

Darstellung eines nach rechts orientierten Elektronenspins durch einen Drehimpuls (Pfeil), der sich zufällig auf einer nach rechts geöffneten Kegelfläche bewegt.

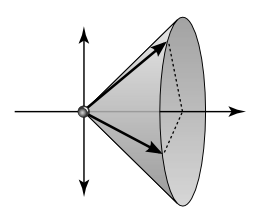
Dieses anschauliche Bild spiegelt sehr schön die Komplementarität der Spinmessung in verschiedenen Richtungen wider: Wenn wir wissen, dass wir bei einer Spinmessung in waagerechter Richtung immer den Spin nach rechts vorfinden, dann orientieren wir die Kegelöffnung nach rechts und erreichen damit, dass in den dazu senkrechten Raumrichtungen die Spinorientierung zufällig ist. Wenn solche Elektronen durch das senkrechte Magnetfeld wandern, ohne dass wir die Ablenkung nach oben oder unten messen, dann bleibt der Kegel unverändert nach rechts geöffnet und die Elektronen werden in einem waagerechten Magnetfeld weiterhin nach rechts abgelenkt. Analog ist es bei einer Spinausrichtung nach links. Wenn wir die Ablenkung nach oben oder unten dagegen messen, so ändert sich dadurch der Kegel: Für die nach oben abgelenkten Elektronen muss er nach der Messung nach oben geöffnet sein und für die nach unten abgelenkten Elektronen nach unten geöffnet. In beiden Fällen ist anschließend die Chance, im waagerechten Magnetfeld nach rechts oder links abgelenkt zu werden, je 50 %.

Wenn unser Zufallscomputer auf dieser anschaulichen Basis das Verhalten eines Spins simuliert, so scheint alles auch ohne Quantenamplituden hervorragend zu funktionieren. Tatsächlich hilft das Kegelbild in vielen Fällen, sich das Verhalten eines Spins zu veranschaulichen − allerdings nicht immer.

c) Verschränkte Spins im Kegelmodell

Für die Darstellung des dritten Triplett-Zustandes ↑↓ + ↓↑ müssen wir einen nach oben und einen nach unten geöffneten Kegel kombinieren, wobei die beiden Drehimpulse bezüglich der senkrechten Richtung immer entgegengesetzt, in waagerechter Richtung jedoch gleich orientiert sind. In senkrechter Richtung verhalten sich die beiden Spins also entgegengesetzt zueinander, in waagerechter Richtung jedoch parallel.

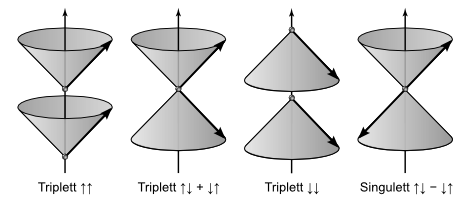
Darstellung der drei Triplett-Zustände und des Singulett-Zustandes im Kegelmodell. Beim Triplett bewegen sich die beiden Drehimpulspfeile gleichphasig, beim Singulett gegenphasig um die senkrechte Achse.

Beim Singulett-Zustand ↑↓ − ↓↑ sind die Kegel genauso ausgerichtet wie beim Triplett-Zustand ↑↓ + ↓↑, aber die beiden Drehimpulse sind immer exakt entgegengesetzt zueinander orientiert. Das Minuszeichen bekommt in diesem Bild eine unmittelbar anschauliche Bedeutung. Egal in welcher Raumrichtung wir messen: die beiden Spins sind beim Singulett-Zustand immer entgegengesetzt ausgerichtet.

Die Tatsache, dass sich die beiden Drehimpulspfeile im Kegelmodell immer synchron zueinander verhalten, bezeichnet man in der Quantenphysik auch als Verschränkung. Die beiden Spins sind also miteinander verschränkt und bilden ein gemeinsames Ganzes: Weiß man etwas über den einen Spin, so weiß man automatisch auch etwas über den anderen Spin.

Konzentrieren wir uns auf den Singulett-Zustand und stellen wir uns vor, dass eine Elektronenquelle immer wieder zwei Elektronen in entgegengesetzte Richtungen aussendet, deren Spins sich in einem solchen Singulett-Zustand befinden. Die beiden Elektronenspins sind also bei jedem emittierten Elektronenpaar garantiert entgegengesetzt zueinander orientiert – egal welche Raumrichtung wir für die Messung wählen und egal, wie weit sich die beiden Elektronen voneinander entfernen. Wenn sie beispielsweise jeweils durch ein senkrechtes inhomogenes Magnetfeld fliegen, so wird eines von ihnen nach oben und das andere nach unten abgelenkt. Welches von ihnen nach oben bzw. nach unten abgelenkt wird, ist dabei nicht vorherbestimmt.

d) Ablenkwahrscheinlichkeit bei einer Spinkippung um 60 Grad

Angenommen, das Magnetfeld ist senkrecht ausgerichtet und der Spin des Elektrons zeigt nach oben (Spin ↑), sodass es garantiert in Richtung Nordpol − der oben liegen soll − abgelenkt wird. Wenn wir das Magnetfeld nun um 60 Grad nach links kippen, sinkt die Wahrscheinlichkeit für das Elektron, auch in diesem Magnetfeld schräg in Richtung Nordpol abgelenkt zu werden. Statt das Magnetfeld um 60 Grad nach links zu kippen, hätten wir auch den Spin des Elektrons um 60 Grad nach rechts kippen und das Magnetfeld senkrecht lassen können − die Ablenkwahrscheinlichkeiten sind dieselben. Bei einem um den Winkel θ nach rechts gekippten Spin ist die Amplitude für die Ablenkung nach oben gegeben durch

wie wir aus Kapitel 6.1 wissen − hier noch einmal die entsprechende Abbildung dazu:

Kippt man den Spin eines Elektrons um den Winkel θ gegen die senkrechte z-Achse, so verändern sich die Wahrscheinlichkeitsamplituden für die senkrechte Spinkomponente wie rechts dargestellt.

Wir müssen also den Cosinus von 60/2 = 30 Grad bilden, was ψ_↑ = √(3/4) ergibt. Für die Wahrscheinlichkeit müssen wir das noch quadrieren, sodass wir folgendes Ergebnis erhalten:

• Die Wahrscheinlichkeit, dass ein Elektron bei zwei Magnetfeldern, die gegeneinander um 60 Grad gekippt sind, beides Mal in Richtung Nordpol oder beides Mal in Richtung Südpol abgelenkt würde, ist nach den Regeln der Quantenmechanik gleich 3/4.

Das steht in klarem Widerspruch zu dem Ergebnis, das wir im Buchkapitel aufgrund der angenommenen inneren Eigenschaften des Elektrons erhalten. Danach sollte diese Wahrscheinlichkeit höchsten 2/3 betragen. Die Vorhersage der Quantenmechanik von 3/4 liegt um 1/12 darüber.